Groupe du Rubik's Cube
Cet article présente un modèle mathématique et une présentation du groupe du Rubik's Cube.
Notations utilisées
- est le groupe des mouvements légaux ou le groupe des états (sans démonter le cube !).
- est le groupe élargi ou le groupe des états étendus (ici on peut démonter le cube, mais les mouvements des sommets et des arêtes doivent rester chaqu'un dans leur camp).
- est l'ensemble des classes d'équivalence pour la congruence modulo n. Il est isomorphe au groupe des n-èmes de tour d'axe donné. On utilisera en particulier C3 pour pivoter un coin du cube, et C2 pour pivoter une arête. On note à savoir .
- est le groupe symétrique d'ordre n. Ses éléments sont les permutations de n objets. Parmi ces permutations, celle de deux objets s'appelle transposition. On utilisera en particulier pour permuter les coins du cube, et pour permuter ses arêtes. La composition des permutations se lit de droite à gauche.
- désigne la signature d'une permutation de .
- Pour toute permutation s élément de , on note P(s) l'automorphisme défini par : . P(s) permute les composantes . s étant une bijection, on remarque que la somme des composantes est invariante : . P est un morphisme du groupe dans le groupe des automorphismes de .
- est le symbole d'un produit semi-direct interne, et celui d'un produit semi-direct externe induit par P.
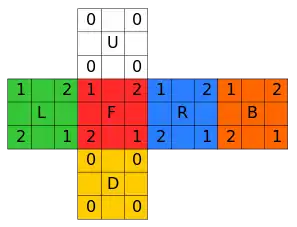
- Les rotations d'un quart de tour, dans le sens des aiguilles d'une montre (sens direct par rapport à un axe entrant dans le cube), sont appelées , , , , , pour les faces droite (right), haut (up), gauche (left), avant (front), arrière (back) et bas (down)[1] - [2].
- On identifie les sommets par 3 coordonnées et les arêtes par 2 ; par exemple FUL est le sommet de face en haut à gauche et BR est l'arête arrière droite[1].
Décomposition des mouvements du cube
Factorisation sommets-arêtes
Un élément de H se décompose naturellement entre son action sur les coins et son action sur les arêtes, ces deux actions étant indépendantes. On introduit les deux sous-groupes Hco et Har constitués respectivement des mouvements agissant sur les coins et laissant invariante chaque arête, et des mouvements agissant sur les arêtes et laissant invariant chaque coin. H est isomorphe au produit direct des groupes [3].
On va maintenant montrer que est isomorphe au produit semi-direct et au produit semi-direct .
L'isomorphisme entre et exprime le fait qu'une action sur les coins se décompose en une permutation des 8 coins (élément de ), et pour chaque coin, d'une rotation possible de 0, 1 ou 2 tiers de tour (pour chaque coin, le groupe de ces rotations est isomorphe à C3)[4].
De même, l'isomorphisme entre et exprime le fait qu'une action sur les arêtes se décompose en une permutation des 12 arêtes, et pour chaque arête, d'une rotation possible de 0 ou 1 demi-tour.
Permutation des arêtes et des sommets
On numérote les sommets du Rubik's cube de 1 à 8 dans cet ordre : FUR, BUR, BUL, FUL, FDR, BDR, BDL, FDL. Les arêtes vont de 1 à 12 : UL, BL, DL, FL, FU, BU, BD, FD, UR, BR, DR, FR.
On définit alors deux morphismes surjectifs de groupes et qui extraient d'un élément de H les permutations des sommets et des arêtes correspondantes, sans tenir compte de leur orientation[3].
Par exemple, en utilisant la notation des cycles, on a et , d'où .
Orientation des arêtes et des sommets
Posons et . Ce sont deux sous-groupes distingués de H. Leurs éléments sont les rotations des coins (identité ou tiers de tour, dans un sens ou dans l'autre) et des arêtes (identité ou demi-tour). Seule l'orientation des cubes change, pas leur position. Ces deux groupes vont permettre de décomposer Hco et Har en les produits semi-directs annoncés.
Changer un cube de position (par exemple mettre FUL en FUR) est une opération ambiguë : dans la position d'arrivée, il y a 3 orientations possibles pour les coins, 2 pour les arêtes. Parmi tous ces mouvements possibles, on en choisit formant deux sous-groupes, Permco et Permar, complémentaires de Rotco et Rotar.
Permco est le groupe des mouvements des coins à orientation constante, isomorphe à . En identifiant Permco à , on peut voir comme un morphisme de H dans Permco. Pour tout g de , est alors un élément de H qui laisse en place chaque coin, mais en les pivotant sur place. C'est donc un élément de . On a donc la décomposition . Cette décomposition est unique du fait que . indique où les coins sont déplacés, et comment ils sont pivotés. La rotation de chaque sommet est donnée par un élément de indiquant de combien de tiers de tour le sommet est pivoté, de sorte que est isomorphe à . On peut représenter par un élément de , la j-ème composante indiquant la rotation que subira le sommet qui arrivera en j par le déplacement dû à g.
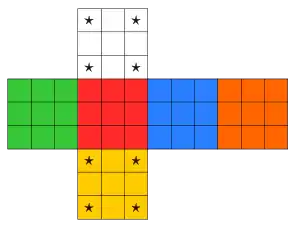
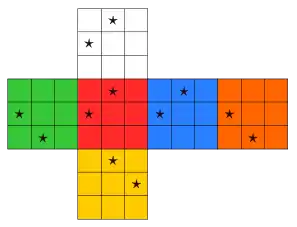
On peut dessiner le choix de Permco en plaçant un marqueur sur chaque coin du Rubik's cube. Un mouvement d'orientation constante est celui qui amène la face marquée de la position de départ sur la face marquée de la position d'arrivée[4]. On peut prendre par exemple le marquage suivant :
pour lequel un mouvement élément de Permco laisse la réunion des faces blanc-jaune globalement invariante. On note ci-dessous par les valeurs 0, 1 ou 2 la valeur à attribuer à la rotation d'un coin en fonction de la place qu'occuperait sa face marquée par une étoile :
Si g et h sont éléments de avec :
alors, on a :
est élément de et est élément de . On n'a pas en géneral ; v n'est donc pas un morphisme de groupe, ce qui empêche d'avoir un produit direct entre Rotco et Permco. Mais la relation est caractéristique d'un produit semi-direct. Ainsi, .
Si a pour composantes , alors a pour composantes . Le remplacement de par son groupe isomorphe transfère le produit semi-direct interne en le produit semi-direct externe .
On remarque par ailleurs que la somme des composantes de est égale à celle de . Il en résulte que la somme des composantes de est égale à la somme de celles de et de celles de . Ainsi, v n'est pas un morphisme, mais la somme des composantes (appelée rotation totale des coins) en est un, à valeurs dans [4].
On opère de même sur les arêtes en choisissant un marquage privilégié de chacune d'elles, ce qui permet de définir leur orientation par le nombre de rotations de 180° permettant de rétablir l'orientation initiale. On peut prendre par exemple :
Comme pour v, w n'est pas un morphisme de groupe, et on a seulement une structure de produit semi-direct , mais la somme de des composantes de w (appelée rotation totale des arêtes) est un morphisme, à valeurs dans .
Théorème fondamental : caractérisation des mouvements légaux
On rappelle que H est le groupe des actions sur le cube de Rubik démontable, et G le groupe des actions sur le cube non démontable (en effectuant des mouvements des faces selon les règles). Pour tout g élément de H, soit vrws la décomposition de g en le produit d'un élément v de (pivotements des coins), r élément de (permutation des coins), w élément de (pivotements des arêtes), s élément de (permutation des arêtes). Alors[5] - [6] :
Autrement dit, G est le noyau du morphisme de H dans , qui, à tout g de H associe le triplet .
Le a) exprime par exemple que, selon les règles du jeu, il est impossible de transposer seulement deux sommets, ou bien seulement deux arêtes. Selon le b), il est impossible de pivoter un coin seul. Deux coins seuls peuvent être pivotés mais en sens inverse l'un de l'autre. Il dit aussi que l'orientation d'un coin est défini de manière unique par l'orientation des 7 autres coins. Le c) exprime qu'il est impossible de pivoter une arête seule. Le pivotement des arêtes s'opère nécessairement par paire. L'orientation d'une arête est définie de manière unique par l'orientation des 11 autres.
Le sens direct de la démonstration consiste à montrer que tout mouvement selon les règles vérifient ces conditions. Le sens réciproque consiste à prouver que, si on se donne une configuration du Rubik's cube vérifiant ces conditions, alors il existe une suite de mouvements selon les règles qui conduit à cette configuration (ou inversement, qui fait passer de cette configuration à la configuration initiale). C'est la description d'un algorithme de résolution du Rubik's cube[7].
Démonstration de la partie directe
Il s'agit de montrer que G est inclus dans . Pour cela, étant un morphisme, il suffit de le prouver pour un système générateur de G, à savoir les six rotations de chacune des faces[7].
En ce qui concerne ε(ρ(g))ε(σ(g)), une rotation d'une face est constitué d'un 4-cycle sur les coins et d'un 4-cycle sur les arêtes. Chaque cycle a pour signature -1 et leur produit fait bien 1.
En ce qui concerne , observons comment chaque rotation de face fait pivoter chacun des coins, (en utilisant le codage 0, 1 et 2 des trois faces de chaque coin donné dans le paragraphe précédent) :
(2,0,0,1,1,0,0,2) (0,0,0,0,0,0,0,0) (0,0,0,0,0,0,0,0) (0,1,2,0,0,2,1,0) (1,2,0,0,2,1,0,0) (0,0,1,2,0,0,2,1)
On constate bien que, pour chaque face, la somme des composantes de est nulle modulo 3.
On peut opèrer une vérification analogue sur les arêtes pour montrer que est nulle modulo 2. Mais il est plus rapide de remarquer que la rotation d'une face induit sur les 2 × 12 = 24 facettes carrées des 12 arêtes une permutation qui est le produit de deux 4-cycles (l'un des 4-cycles permute circulairement 4 facettes, l'autre 4-cycle permute circulairement 4 autres facettes, adjacentes aux 4 premières). Il en résulte que la signature de la permutation des 24 facettes vaut 1, et qu'il en est de même par composition pour un mouvement quelconque du Rubik's cube. Or cette signature n'est autre que . Il en résulte que est nulle modulo 2[7].
Démonstration de la réciproque
Il s'agit de montrer que est inclus dans G. Pour cela, partant d'une configuration g appartenant à , on lui applique une suite S de rotations des faces appartenant à G de façon que . Cela prouve que g est le symétrique de S, donc est élément de G[7].
Les mouvements des faces à effectuer seront donnés ici par une suite de lettres : majuscules F, R, L, B, U, D pour une rotation dans le sens des aiguilles d'une montre, minuscules f, r, l, b, u, d pour le sens inverse. La composition des mouvements se fera dans ce paragraphe dans le sens de la lecture du mot ainsi formé, i.e. de gauche à droite. Ainsi, le mouvement "FUl" est constitué d'une rotation dans le sens des aiguilles d'une montre de la face F, suivie de la face U, et on termine par une rotation en sens inverse de la face L. La suite S est construite en mettant d'abord en place les arêtes, puis les coins, puis en pivotant convenablement les arêtes, puis les coins.
Mise en place des arêtes : pour tout couple d'arêtes, il existe un élément de G qui transpose ces deux arêtes, en laissant les autres arêtes en place (à pivotement près)[8]. Par exemple "uFULulf" transpose deux arêtes de la face U[9]. Comme les transpositions engendrent le groupe symétrique, cela prouve qu'il existe un élément de G qui dispose les arêtes à leur place.
Mise en place des coins : Compte tenu de la condition de parité a) sur la signature des permutations des arêtes et des coins, si les arêtes sont en place, cela signifie que les coins sont permutés par une permutation paire. Or ces permutations sont engendrées par les 3-cycles (permutation circulaire de trois coins). Pour mettre les coins en place par un mouvement élément de G, il suffit donc de montrer que, pour tout triplet de coins, il existe un élément de G qui permute ces trois coins tout en laissant les autres coins et les arêtes à leur place. C'est effectivement le cas. Par exemple, le mouvement "LurUluRU" permute trois coins de la face U tout en laissant tous les autres cubes à leur place, sans modifier aucun autre cube[10].
Pivotement des arêtes : Compte tenu de la condition c) sur le pivotement des arêtes, on peut pivoter convenablement les arêtes en opérant successivement sur deux arêtes à la fois. Pour tout couple d'arêtes, il existe un élément de G qui se borne à pivoter deux arêtes[8]. Par exemple, le mouvement "BddbbdBDBddflbLF" pivote deux arêtes adjacentes de la face D sans modifier aucun autre cube[11].
Pivotement des coins : Compte tenu de la condition b) sur le pivotement des coins, on peut pivoter convenablement les coins en opérant successivement sur deux coins à la fois, les rotations étant de sens opposé sur ces deux coins. Pour tout couple de coins, il existe un élément de G satisfaisant ces conditions[12]. Par exemple, le mouvement "uBULBlFLblubUf" pivote en sens inverse deux coins de la face U[13].
Une fois ces opérations terminées, le cube est remis en place et on a prouvé que la configuration initiale g est bien élément de G.
Calcul du cardinal du groupe des mouvements du Rubik's Cube
On rappelle qu'on a introduit un morphisme de H dans , qui, à une configuration g du cube démontable associe le triplet constitué du produit des signatures des permutations sur les coins et les arêtes, la rotation totale des coins et la rotation totale des arêtes. Le noyau de est le groupe G des mouvements du Rubik's cube.
Ce morphisme est surjectif car, pour tout élément de , on peut trouver une configuration g de H antécédent par de cet élément. Il suffit pour cela de pivoter un coin et une arête de façon adéquate et éventuellement de permuter deux coins (on rappelle que, dans H, tous les mouvements sont possibles). Comme est de cardinal 12, il en résulte que G est un sous-groupe de H d'indice 12, les classes de G étant les gG avec g parcourant dans H un sous-ensemble de 12 représentants d'antécédents par des 12 éléments de .
Par conséquent, le cardinal de G est le douzième de celui de H[3]. (C'est une variante du théorème de Lagrange ou de la formule des indices). Or le cardinal de H est (produit du nombre de permutations des coins par le nombre de pivotement des coins par le nombre des permutations des arêtes par le nombre de pivotement des arêtes), donc celui de G est :
soit environ 43 milliards de milliards de combinaisons.
On peut aussi dire qu'il y a pivotements d'arêtes possibles (l'orientation de la dernière arête étant alors imposée par la condition c)), pivotements de coins possibles (l'orientation du dernier coin étant imposé par la condition b)), placements possibles des huit sommets, mais seulement placements possibles des douze arêtes en raison de la condition de parité donnée par la condition a). Le total redonne le résultat précédent[14] - [15].
Générateurs et relations
Propriétés particulières
Comme précédemment, on donne les mouvements des faces à effectuer par une suite de lettres, la composition s'effectuant ici de gauche à droite : majuscules F, R, L, B, U, D pour une rotation dans le sens des aiguilles d'une montre, prime F', R', L', B', U', D' pour le sens inverse.
- On peut engendrer le groupe G en autorisant seulement les rotations de cinq faces données. En effet, le mouvement "R'LF'2B'2R'LD'R'LF'2B'2R'L", dû à David Benson, permet de tourner la face supérieure en utilisant uniquement les autres faces[16].
- L'ordre maximal d'un élément de G est 1260. Il est obtenu par exemple par le mouvement "R'B'2DU'D"[17].
- Le groupe G peut être engendré par deux mouvements seulement, par exemple "L'2B'R'DL" et "U'F'R'U'RUF"[18].
Présentation du problème
D’après les notations utilisées pour étudier le Cube, le problème peut se présenter sous deux formes. On peut le traiter en utilisant des notations totalement mathématiques ou alors le traiter sous forme de mots puisque chacune des lettres R,U etc. correspond à une permutation (voir numérotation du Cube). Il existe donc une fonction surjective de l’ensemble des mots sur X = {R,L,U,D,F,B} vers l’ensemble des permutations du Cube. Pour une permutation, la longueur est définie comme étant, en partant du Cube résolu, le nombre minimum de mouvement (= générateurs considérés) à effectuer pour obtenir la permutation.
Première application : nombre minimum de mouvements
À partir de ces mouvements, on peut construire un arbre où chaque nœud représente une position du cube (la permutation appliquée au cube résolu). En partant de l’identité, on peut construire une suite () qui à chaque étape est égal au nombre de position possible du cube réalisable avec n mouvements de base. On a et ensuite pour tout n, on a . En effet, pour plus de précision dans le calcul, il ne faut pas compter toutes les permutations qui permettraient de revenir à une position déjà atteinte. Pour cela, il faut donc fixer des conditions (on compte ici les mouvements de la tranche du milieu) : on ne compte pas les positions obtenues par deux mouvements consécutifs sur une même face ni trois mouvements autour du même axe. Dans une situation donnée, il ne reste plus que 12 dans une position de mouvements possible plus les 18 que l’on peut effectuer sur qui correspond aux positions où l’on n’a pas répété les mouvements (ou encore les positions où l’on a répété les mouvements pour revenir à une identité). On peut ensuite calculer le terme général de la suite puis l’égaler à N, le nombre de positions totales possibles du cube afin de déterminer n. On trouve alors n = 17.3 ce qui montre qu’il existe une position du cube qui ne peut pas être atteinte en moins de 18 mouvements. Il a même été prouvé qu'une position (le centre du cube) nécessite 20 mouvements.(Voir Optimal solutions for Rubik's Cube)
Générateurs et relations : présentation d’un groupe
Soit X un ensemble fini avec n = card X. Le groupe libre sur les générateurs éléments de , noté est le groupe des mots réduits de .
Soit Y un groupe de mots réduits sur X. Soit R le plus petit sous groupe normal de contenant Y. R constitue l’ensemble des relations de . Le quotient Fn/R est un groupe ; c’est le plus grand groupe qui satisfait ces relations. On dit qu'il a pour générateurs l’ensemble X et pour relations l'ensemble Y. Un ensemble de générateurs et de relations est appelé une présentation.
En termes de notation, un élément r de R est noté sous forme d’une équation de la forme r = 1.
Exemple : le groupe cyclique d’ordre n possède un générateur x et une relation donc on a et . admet donc comme présentation : Le groupe diédral d’ordre n a pour présentation
Recherche d’une présentation de Cn
m ⋊ 𝕾n+1
m ⋊ 𝕾n+1
Il faut d’abord chercher les représentations des groupes symétriques et des groupes cycliques. Pour le groupe symétrique d’ordre n+1, on a: avec Dans le cas où n=4, la matrice est :
Pour le produit cartésien du groupe cyclique d'ordre m, on a :
Pour le groupe symétrique, on peut associer à chaque transposition (de deux indices consécutifs) une matrice de permutation de taille (n+1)*(n+1) autrement dit
On peut aussi identifier avec le produit cartésien où
On a alors les relations suivantes entre les
On peut alors démontrer la propriété suivante :
Démonstration : si on appelle la représentation présentée ci-dessus. Le but de la démonstration est bien sûr de montrer . Pour cela on considère le morphisme qui associe les générateurs de avec les générateurs de . Par définition de l'application, est surjective. Pour prouver l'injectivité, on note . En notant , on a d'après le théorème de Lagrange : .
En considérant maintenant , est un sous groupe normal à . En effet, chaque renvoie un générateur de H sur un produit de générateurs de H ou sur son inverse. Comme H est un groupe, on obtient que . On a donc . Si est une relation de P, le mot écrit dans le groupe quotient devient un mot qui ne contiendra plus que des relations du type . On peut montrer ainsi que (cette partie de la démonstration sera précisée).
Ainsi, on a ce qui montre et ainsi d'où . est donc injectif donc bijectif.
Liens externes
- Pierre Colmez, « Le Rubik's Cube, groupe de poche »
- W. D. Joyner, « Mathematics of the Rubik's cube »,
- Matthieu Barreau, « Une analyse du Cube Hongrois »,
Bibliographie
- David Singmaster, Notes on Rubik's cube, Enslow Publishers,
- Edward C. Turner et Karen F. Gold, « Rubik's Groups », The American Mathematical Monthly, vol. 92, no 9, , p. 617-629 (DOI 10.1080/00029890.1985.11971700, lire en ligne)
- André Warusfel, Réussir le Rubik's cube, Denoël,
Notes et références
- (Singmaster, p. 4)
- (Warusfel, p. 33)
- (Colmez, p. 2)
- (Colmez, p. 3)
- (Colmez, p. 4)
- (Warusfel, p. 152-160)
- (Colmez, p. 5)
- (Colmez, p. 6)
- (Warusfel, p. 186)
- (Warusfel, p. 182)
- (Warusfel, p. 146). Ce mouvement a été découvert par Morwen Thistlethwaite (en)
- (Colmez, p. 7)
- (Warusfel, p. 184)
- http://ronan.terpereau.perso.math.cnrs.fr/Projet-L3/analyse_cube_hongrois.pdf, Proposition 3
- (Warusfel, p. 161)
- (Warusfel, p. 142)
- (Warusfel, p. 145)
- (Warusfel, p. 144)