Graphe série-parallèle
En théorie des graphes, les graphes série-parallèle sont des graphes avec deux sommets distingués, la source et le puits, et formés récursivement par deux opérations qui sont la composition en série et la composition parallèle. Ces graphes peuvent servir pour modéliser des circuits électriques en série et en parallèle .
Définition et terminologie
Dans ce contexte, le terme graphe signifie multigraphe. Il existe plusieurs façons équivalentes de définir des graphes série-parallèle.
Une première définition
La définition suivante suit essentiellement celle utilisée par David Eppstein[1].
- Un graphe à deux sommets terminaux (TTG) est un graphe avec deux sommets distincts s et t appelés respectivement source et puits.
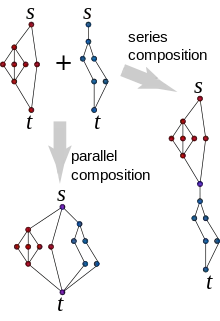
- La composition parallèle de deux TTG X et Y est le TTG Z formé à partir de l'union disjointe des graphes X et Y en fusionnant les sources de X et Y pour créer la source de Z et en fusionnant les puits de X et Y pour créer le puits de Z.
- La composition en série de deux TTG X et Y est le TTG Z créé à partir de l'union disjointe des graphes X et Y en fusionnant le puits de X avec la source de Y. La source de X devient la source de Z et le puits de Y devient le puits de Z .
Définition 1. Un graphe série-parallèle (SP-graphe) est un graphe qui peut être construit par une suite de compositions en séries et parallèles à partir d'un ensemble de copies d'un graphe à deux sommet reliés par une arête.
De la même manière, on peut définir des graphes orientés série-parallèle, construits à partir de copies de graphes à un seul arc, avec des arcs dirigés de la source vers le puits.
Courcelle et Engelfriet[2] donnent la définition sous forme de grammaire de graphes :
- S= (S//S)∪(S•S)∪{e}.
Une autre définition
La définition suivante décrit la même classe de graphes[3] :
Définition 2. Un graphe est un SP-graphe, s'il peut être transformé en K2, le graphe complet à 2 sommets, par une séquence d'opérations suivantes :
- remplacement d'une paire d'arêtes parallèles par une seule arête qui relie leurs extrémités communes ;
- remplacement d'une paire d'arêtes incidentes à un sommet de degré 2 autre que s ou t par une seule arête.
La même définition, formulée de façon constructive, s'énonce comme suit[4] : on part du graphe à deux sommets reliés par une arête, et on itère les opérations suivantes :
- une arête (x,y) est remplacée par deux arêtes (x,z) et (z,y), où z est un nouveau sommet (opération de sérialisation) ;
- une arête (x,y) est dupliquée[5] (opération de parallélisation).
Propriétés
Tout graphe série-parallèle a une largeur arborescente au plus 2 et une largeur de branche au plus 2[6]. En effet, un graphe a une largeur arborescente au plus 2 si et seulement s'il a une largeur de branche au plus 2, si et seulement si chaque composante biconnexe est un graphe série-parallèle[7] - [8]. Les graphes série-parallèle maximaux, graphes auxquels aucune arête supplémentaire ne peut être ajoutée sans détruire leur structure série-parallèle, sont exactement les 2-arbres.
Les graphes série-parallèle 2-connexes sont caractérisés par la propriété qu'aucun sous-graphe n'est homéomorphe à K4[6]
Les graphes série-parallèle peuvent également être caractérisés par leurs décompositions auriculaires (en)[1].
Complexité algorithmique
Les SP-graphes peuvent être reconnus en temps linéaire[9] et leur décomposition série-parallèle peut également être construite en temps linéaire.
En plus d'être un modèle de certains types de réseaux électriques, ces graphes sont intéressants en théorie de la complexité de calcul, car un certain nombre de problèmes usuels sur les graphes se résolvent en temps linéaire pour les SP-graphes[10] ; ces problèmes comprennent la recherche d'un couplage maximum, d'un ensemble indépendant maximal, d'un ensemble dominant minimal et la complétion hamiltonienne (en). Certains de ces problèmes sont NP-complets pour les graphes généraux. La solution tire profit du fait que si la réponse à l'un de ces problèmes est connue pour deux SP-graphes, alors on peut trouver rapidement la réponse pour leurs compositions en série et parallèle.
Généralisations
Les graphes série-parallèle généralisés (GSP) sont une extension des SP-graphes avec la même complexité algorithmique pour les problèmes énumérés plus haut. La classe des GSP-graphes comprend les SP-graphes et les graphes planaires extérieurs.
Les GSP-graphes peuvent être définis à partir de la définition 2 augmentée d'une troisième opération qui est la suppression d'un sommet pendant (sommet de degré 1). De manière équivalente, la définition 1 peut être complétée avec l'opération de fusion suivante : la fusion à la source S = M (X, Y) de deux TTG X et Y est un TTG créé à partir de l'union disjointe des graphes X et Y en fusionnant la source de X avec la source de Y. Autrement dit, la source et le puits de X deviennent respectivement la source et le puits de S.
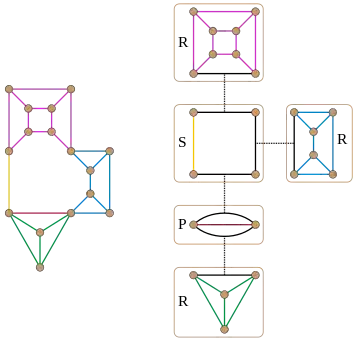
Un arbre SPQR est une structure arborescente qui peut être définie pour un graphe sommet-connexe arbitraire ; à chaque sommet est associé un graphe ou multigraphe. Il a des nœuds source S, qui sont analogues aux opérations de composition en série dans les graphes série-parallèle, des nœuds puits P, qui sont analogues aux opérations de composition parallèle dans les graphes série-parallèle, et des nœuds R, qui ne correspondent pas aux compositions série-parallèle. Un graphe biconnexe est série-parallèle si et seulement s'il n'y a pas de nœuds R dans son arbre SPQR.
Voir aussi
- Graphe de seuil
- Cographe
- Polytope de Hanner
- Ordre partiel série-parallèle
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Series-parallel graphs » (voir la liste des auteurs).
- David Eppstein, « Parallel recognition of series-parallel graphs », Information and Computation, vol. 98, no 1, , p. 41–55 (DOI 10.1016/0890-5401(92)90041-D, lire en ligne).
- Bruno Courcelle et Joost Engelfriet, Graph structure and monadic second-order logic, a language theoretic approach, Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications », , 728 p. (ISBN 9780521898331, présentation en ligne).
- Richard James Duffin, « Topology of Series-Parallel Networks », Journal of Mathematical Analysis and Applications, vol. 10, no 2, , p. 303–313 (DOI 10.1016/0022-247X(65)90125-3).
- Bruno Bachelet, « Modélisation et optimisation de problèmes de synchronisation dans les documents hypermedia », Thèse de doctorat, Université Blaise Pascal - Clermont-Ferrand II, , section 5.1.1. « Graphe série-parallèle, SP-graphe ».
- Opération possible dans le multigraphe.
- Andreas Brandstädt, Van Bang Le et Jeremy P. Spinrad, Graph classes: a survey, vol. 3, Philadelphia, PA, Society for Industrial and Applied Mathematics, coll. « SIAM Monographs on Discrete Mathematics. and Applications », (ISBN 978-0-898714-32-6, zbMATH 0919.05001, lire en ligne), p. 172–174.
- H. Bodlaender, « A partial k-arboretum of graphs with bounded treewidth », Theoretical Computer Science, vol. 209, nos 1–2, , p. 1–45 (DOI 10.1016/S0304-3975(97)00228-4).
- Rhiannon Hall, James Oxley, Charles Semple et Geoff Whittle, « On matroids of branch-width three », Journal of Combinatorial Theory Series B, vol. 86, no 1, , p. 148–171 (DOI 10.1006/jctb.2002.2120).
- Jacobo Valdes, Robert Tarjan et Eugene Lawler, « The recognition of series parallel digraphs », SIAM Journal on Computing, vol. 11, no 2, , p. 289–313 (DOI 10.1137/0211023)
- K. Takamizawa, Takao Nishizeki et Nobuji Saito, « Linear-time computability of combinatorial problems on series-parallel graphs », Journal of the ACM, vol. 29, no 3, , p. 623–641 (DOI 10.1145/322326.322328)