Accueil🇫🇷Chercher

Arbre SPQR

En théorie des graphes, un arbre SPQR est une structure de données arborescente utilisée en informatique, et plus spécifiquement en algorithmique de graphes, pour représenter les composantes triconnexes d'un graphe. L'arbre SPQR d'un graphe peut être construit en temps linéaire[1] - [2] ; plusieurs applications dans les algorithmes de graphes dynamiques et dans le tracé de graphes utilisent cette structure de données.

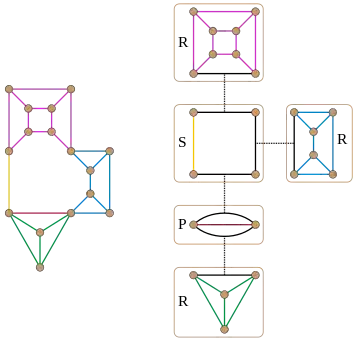
Un graphe et son arbre SPQR. Les lignes noires pointillés sont des arêtes virtuelles, représentées en noir; les arêtes restantes sont colorées d'après la composant triconnexe à laquelle elles appartiennent.

Les structures de base sous-jacentes à unarbre SPQR, sont les composantes triconnexes d'un graphe et la relation entre cette décomposition et les plongements planaires d'un graphe planaire; ces relations ont d'abord été étudiés par Saunders Mac Lane[3] ; ces structures ont été utilisées dans des algorithmes efficaces par plusieurs autres chercheurs[4] avant leur formalisation en termes d'arbre SPQR par Di Battista et Tamassia[5] - [6] - [7].

Structure

Un arbre SPQR se présente sous la forme d'un arbre non enraciné dans lequel à chaque nœud x est associé un graphe ou multigraphe non orienté G x, une composante du graphe donné. Les nœuds sont reliés par des arêtes « virtuelles » qui relient les graphes associés, eux aussi dotés d'arêtes virtuelles.

Un nœud, et le graphe qui lui est associé, peut être de l'un des quatre types suivants, correspondant aux initiales SPQR:

  • Dans un nÅ“ud de type S, le graphe associé est un graphe cycle avec au moins trois sommets et arêtes. Ce cas est analogue à la composition en série dans les graphes série-parallèle ; la lettre « S » signifie « série »[5].
  • Dans un nÅ“ud de type P, le graphe associé est un graphe dipolaire, un multigraphe avec deux sommets et au moins trois arêtes ; c'est le dual planaire d'un graphe cyclique. Ce cas est analogue à la composition parallèle dans graphes série-parallèle ; la lettre « P » signifie « parallèle[5].
  • Dans un nÅ“ud de type Q, le graphe associé a une seule arête réelle. Ce cas permet de prendre en compte le graphe trivial qui n'a qu'une seule arête. Dans certains articles, ce type de nÅ“ud n'apparaît pas dans les arbres SPQR des graphes qui ont plus d'une arête; dans d'autres, toutes les arêtes qui ne sont pas virtuelles doivent être représentées par des nÅ“uds Q avec une arête réelle et une arête virtuelle, et les arêtes des autres types de nÅ“uds doivent toutes être virtuelles.
  • Dans un nÅ“ud de type R, le graphe associé est un graphe triconnexe qui n'est ni un cycle ni un dipôle. Le R signifie «rigide»: dans l'application des arbres SPQR aux plongement de graphe planaire, le graphe associé à un nÅ“ud R a un plongement planaire unique[5].

À chaque arête xy entre deux nœuds de l'arbre SPQR sont associée à deux arêtes virtuelles orientées, dont l'une est une arête dans G x et l'autre est une arête dans G y . Chaque arête d'un graphe G x ne peut être une arête virtuelle que pour au plus une arête d'arbre SPQR.

Un arbre SPQR A représente un graphe biconnexe G A, formé comme suit. Chaque fois que l'arête d'arbre SPQR xy associe l'arête virtuelle ab de G x à l'arête virtuelle cd de G y, on forme un seul graphe plus grand en fusionnant a et c en un seul super-sommet, en fusionnant b et d en un autre super-sommet unique, et en supprimant les deux arêtes virtuelles. Autrement dit, le graphe obtenu est la somme de clique (en) de G x et G y. L'exécution de cette étape de regroupement sur chaque arête de l'arbre SPQR produit le graphe G A ; l'ordre d'exécution des étapes de regroupement n'affecte pas le résultat. Chaque sommet de l'un des graphes G x peut être associé de cette manière à un sommet unique de G A, le super-sommet dans lequel il a été fusionné.

En règle générale, dans une arborescence SPQR deux nœuds de type S ne sont pas adjacents, ni deux nœuds P, car si une telle adjacence implique que les deux nœuds peuvent être fusionnés en un seul nœud plus grand. Avec cette hypothèse, l'arbre SPQR est uniquement déterminé à partir de son graphe. Lorsqu'un graphe G est représenté par un arbre SPQR sans nœuds P adjacents et sans nœuds S adjacents, alors les graphes G x associés aux nœuds de l'arbre SPQR sont les composantes triconnexes de G..

Construction

L'arbre SPQR d'un graphe biconnexe donné peut être construit en temps linéaire[1] - [2].

La construction des composantes triconnexes d'un graphe en temps linéaire a été décrite Hopcroft et Tarjan en 1973[1]. Sur la base de cet algorithme, Di Battista et Tamassia ont conjecturé en 1996[7] que la structure arborescente SPQR complète, et pas seulement la liste des composants, peut être construite en temps linéaire. Après un premier algorithme plus lent pour les arbres SPQR implémenté dans la bibliothèque GDToolkit, Gutwenger et Mutzel[2] ont fourni en 2001 la première implémentation en temps linéaire.

L'algorithme de Gutwenger et Mutzel comprend les étapes générales suivantes :

  1. Tri des arêtes du graphe en fonction des paires d'indices numériques de leurs extrémités, en utilisant une variante du tri par base qui effectue deux passes de tri par paquets, une pour chaque extrémité. Après cette étape de tri, les arêtes parallèles entre les deux mêmes sommets sont adjacentes l'une à l'autre dans la liste triée et peuvent être groupées en un nœud P de l'arbre SPQR à construire, et ainsi le graphe restant est un graphe simple.
  2. Partition du graphe en composantes séparées ; ce sont des graphes qui peuvent être formés en trouvant une paire de sommets de séparation. On divise le graphe à ces deux sommets en deux graphes plus petits (avec une paire liée d'arêtes virtuelles ayant les sommets de séparation comme points d'extrémité), et on répète ce processus de fractionnement jusqu'à ce qu'il n'y ait plus de paires de séparation. La partition trouvée de cette manière n'est pas définie de manière unique, car les parties du graphe qui devraient devenir des nœuds S de l'arbre SPQR sont subdivisées en plusieurs triangles.
  3. Étiquetage de chaque composant séparé soit d'un P (un composant scindé à deux sommets avec plusieurs arêtes), soit d'un S (un composant scindé sous la forme d'un triangle) ou d'un R (tout autre composant scindé). Tant qu'il existe deux composants séparés qui partagent une paire liée d'arêtes virtuelles et que les deux composants sont de type S ou les deux de type P, on les fusionne en un seul composant plus grand du même type.

Pour trouver les composantes séparées, Gutwenger et Mutzel utilisent dans leur article une recherche en profondeur pour trouver une structure qu'ils appellent un palmier; il s'agit d'un arbre de recherche en profondeur d'abord avec ses arêtes orientées dans le sens s'éloignant de la racine de l'arbre pour les arêtes appartenant à l'arbre, et vers la racine pour toutes les autres arêtes. Ils obtiennent ensuite une numérotation en préordre particulière des nœuds dans l'arborescence et utilisent certains motifs de cette numérotation pour identifier des paires de sommets qui peuvent séparer le graphe en composants plus petits. Lorsqu'un composant est trouvé de cette manière, une pile est utilisée pour identifier les arêtes qui doivent faire partie du nouveau composant.

Utilisation

Détermination de coupes à deux sommets

Avec l'arbre SPQR d'un graphe G (sans nœuds de type Q), il est simple de trouver les paires de sommets u et v dans G dont la suppression déconnecte le graphe, et les composantes connexes des graphes restants ; on procède comme suit :

  • (R) Si les sommets u et v sont les deux extrémités d'une arête virtuelle dans le graphe associé à un nÅ“ud de type R, les deux composantes sont représentées par les deux sous-arbres de l'arbre SPQR formé en supprimant l'arête d'arbre SPQR correspondante.
  • (P) Si les sommets u et v sont les deux sommets du graphe associés à un nÅ“ud P qui a au moins deux arêtes virtuelles, les composantes formées par la suppression de u et v sont représentées par des sous-arbres de l'arbre SPQR, avec un sous-arbre pour chaque arête virtuelle du nÅ“ud.
  • (S) Si les sommets u et v sont deux sommets du graphe associés à un nÅ“ud S qui non adjacents ou ont une arête uv virtuelle, on pocède selon les cas : si l'arête est virtuelle, la paire ( u, v ) appartient également à un nÅ“ud de type P et R et les composants sont tels que décrits ci-dessus ; si les deux sommets ne sont pas adjacents, alors les deux composantes sont représentées par deux chemins du graphe cycle associés au nÅ“ud S et aux nÅ“uds d'arbre SPQR attachés à ces deux chemins.

Représentation de tous les plongements de graphes planaires

Un graphe planaire triconnexe, possède un plongement planaire unique au choix près de la face externe et de l'orientation du plongement : les faces du plongement sont exactement les cycles non séparants du graphe. En revanche, dans un graphe planaire avec sommets et arêtes étiquetés qui est biconnexe sans être triconnexe, il y a un plus de liberté dans la détermination d'un plongement planaire. Plus précisément, chaque fois que deux nœuds de l'arborescence SPQR du graphe sont connectés par une paire d'arêtes virtuelles, on peut inverser l'orientation de l'un des nœuds (en le remplaçant par son image miroir) par rapport à l'autre. De plus, dans un nœud P de l'arbre SPQR, les différentes parties du graphe connectées aux arêtes virtuelles du nœud P peuvent être permutées arbitrairement. Toutes les représentations planaires peuvent être décrites de cette manière [8].

Voir également
  • Arbre de blocs, une structure arborescente similaire pour les composantes biconnexes
  • Arbre de Gomory-Hu, une structure arborescente différente qui caractérise la connexité des arêtes d'un graphe
  • Décomposition arborescente, une généralisation (qui n'est pas unique) aux coupes plus grandes.

Notes et références
  1. Hopcroft et Tarjan (1973).
  2. Gutwenger et Mutzel (2001).
  3. Mac Lane 1937.
  4. Par exemple Hopcroft et Tarjan 1973 et Bienstock et Monma 1988, articles cités par Di Battista and Tamassia.
  5. Di Battista et Tamassia (1989).
  6. Di Battista et Tamassia (1990).
  7. Di Battista et Tamassia (1996).
  8. Mac Lane (1937).

Bibliographie
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.