Cographe
Un cographe est, en théorie des graphes, un graphe qui peut être généré par complémentation et union disjointe à partir du graphe à un nœud.
La plupart des problèmes algorithmiques peuvent être résolus sur cette classe en temps polynomial, et même linaire, du fait de ses propriétés structurelles.
Définitions et caractérisations
Cette famille de graphe a été introduite par plusieurs auteurs indépendamment dans les années 1970 sous divers noms, notamment D*-graphes, hereditary Dacey graphs et 2-parity graphs[1].
Définition
Un cographe est un graphe simple qui peut-être construit de manière récursive selon les règles suivantes :
- le graphe à un sommet est un cographe,
- le complémentaire d'un cographe est un cographe,
- l'union de deux cographes est un cographe.
Définition utilisant l'opération join
Le "join" de deux graphes disjoints et , est l'opération qui consiste à créer un nouveau graphe , où et . Cette opération est en fait le complémentaire de l'union des complémentaires.
Un cographe est alors un graphe qui peut être formé à partir des graphes à un sommet, par "join" et par union.
Caractérisations
Il existe de nombreuses caractérisations des cographes, notamment :
- les cographes sont les graphes -free, c'est-à-dire ceux qui n'ont pas le chemin sur quatre sommets comme sous-graphe induit[2];
- les cographes sont graphes pour lesquels tous les sous-graphes induits non triviaux possèdent deux sommets ayant le même voisinage.
- les cographes sont les graphes d'inversions des permutations séparables.
Coarbre
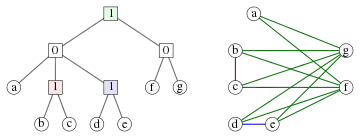
Un coarbre décrit un cographe, grâce aux opérations qui sont nécessaires pour les construire.
Les feuilles représentent les nœuds du cographe, et les nœuds internes représentent des opérations. Les nœuds étiquetés par un 0 représentent l'union des cographes représentés par les sous-arbres et ceux étiquetés par un 1 représentent le "join" de ces cographes. Il existe une arête entre deux nœuds de l'arbre si et seulement si le plus petit ancêtre commun à ces nœuds est étiqueté par 1.
Cette représentation est unique. C'est une manière compacte de représenter les cographes.
De plus en échangeant les 1 et les 0, on obtient le coarbre du graphe complémentaire.
Propriétés mathématiques et inclusions
- La famille des cographes est stable par sous-graphes induits[3];
- Les cographes sont des graphes parfaits.
- Les graphes de Turán sont des cographes.
- les cographes sont des graphes de permutation et des graphes de comparabilité.
Propriétés algorithmiques
Les cographes peuvent être reconnus en temps linéaire[4]. La plupart des problèmes classiques peuvent être résolus en temps linéaire sur cette classe, par exemple les problèmes liés aux cliques et aux cycles hamiltoniens[5]. Le problème de la coupe maximum est polynomial sur cette classe[6].
Dans un contexte de calcul distribué synchrone, la caractérisation par 4-chemin exclus permet de reconnaitre les cographes en un nombre constant de tours[7].
Notes et références
- voir notamment (Jung 1978), (Sumner 1974) et (Burlet et Uhry 1984)
- Voir (Corneil, Lerchs et Burlingham 1981) et (Seinsche 1974).
- Cela découle directement de la caractérisation P4-free.
- (Corneil, Perl et Stewart 1985)
- Voir la page associé sur Information System on Graph Classes and their Inclusions
- Voir (Bodlaender et Jansen 2000)
- (Fraigniaud, Halldorsson et Korman 2012)
Bibliographie
- H. A. Jung, « On a class of posets and the corresponding comparability graphs », Journal of Combinatorial Theory, Series B, vol. 24, no 2, , p. 125–133 (DOI 10.1016/0095-8956(78)90013-8).
- D. P. Sumner, « Dacey graphs », J. Austral. Math. Soc., vol. 18, no 4, , p. 492–502 (DOI 10.1017/S1446788700029232).
- M. Burlet et J. P. Uhry, « Topics on Perfect Graphs (Parity Graphs) », Annals of Discrete Mathematics, vol. 21, , p. 253–277.
- D. G. Corneil, H. Lerchs et L. Stewart Burlingham, « Complement reducible graphs », Discrete Applied Mathematics, vol. 3, no 3, , p. 163–174 (DOI 10.1016/0166-218X(81)90013-5).
- D. G. Corneil, Y. Perl et L. K. Stewart, « A linear recognition algorithm for cographs », SIAM Journal on Computing, vol. 14, no 4, , p. 926–934 (DOI 10.1137/0214065, MR 0807891).
- Hans L. Bodlaender et Klaus Jansen, « On the Complexity of the Maximum Cut Problem », Nord. J. Comput., vol. 7, no 1, , p. 14-31.
- D. Seinsche, « On a property of the class of n-colorable graphs », Journal of Combinatorial Theory, Series B, vol. 16, no 2, , p. 191-193 (DOI 10.1016/0095-8956(74)90063-X, MR 0337679).
- Pierre Fraigniaud, Magnus M Halldorsson et Amos Korman, « On the impact of identifiers on local decision », dans Principles of Distributed Systems, , p. 224 -238





