Graphe de comparabilité
Dans la théorie des graphes, un graphe de comparabilité est un graphe non orienté qui relie les paires d'éléments qui sont comparables les uns aux autres dans un ordre partiel donné. On les trouve aussi sous le nom de transitively orientable graphs, partially orderable graphs, et containment graphs.
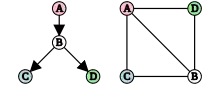
Relations avec d'autres classes
Les graphes de comparabilité sont des graphes parfaits[1].
Les cographes sont des graphes de comparabilité
Les graphes qui sont de comparabilité et dont le complémentaire est aussi de comparabilité sont exactement les graphes de permutations.
Aspects algorithmiques
Les graphes de comparabilité peuvent être reconnus en temps linéaire en calculant une orientation[2]. Plusieurs problèmes NP-complet dans le cas général peuvent être résolus en temps polynomial pour ces graphes comme la coloration, le problème du sandwich de graphes ou même en temps linéaire, comme le problème de la clique maximum[3].
Notes et références
- Alain Hertz, « Quelques classes de graphes », sur GERAD.
- R. M. McConnell et J. Spinrad, « Linear-time transitive orientation », dans 8th ACM-SIAM Symposium on Discrete Algorithms, , p. 19-25.
- « Comparability graph », sur Information System on Graph Classes and their Inclusions.
Liens externes
- « Comparability graph », sur Information System on Graph Classes and their Inclusions.