Graphe de permutation
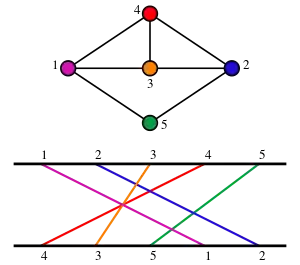
En théorie des graphes, un graphe de permutation est un graphe non orienté dont les sommets représentent les éléments d'une permutation, et dont les arêtes relient les paires de sommets qui sont inversés dans la permutation. On peut aussi définir les graphes de permutations de manière géométrique : ce sont les graphes d'intersections de segments dont les extrémités sont sur deux droites parallèles.
Définitions et caractérisations
On définit les graphes de permutation de la manière suivante. Les sommets représentent les éléments d'une permutation, et les arêtes relient les paires de sommets dont les éléments sont inversés dans la permutation[1].
Autre caractérisations :
- les graphes de permutation sont les graphes d'intersection de segments dont les extrémités sont disposés sur deux droites parallèles.
- les graphes de permutation sont les graphes qui sont des graphes de comparabilité et dont le complémentaire est aussi de comparabilité[2].
Relations avec d'autres classes
La classe des graphes de permutation est incluse dans les graphes de comparabilité, dans les circle graphs (en), et dans les trapezoid graphs (en).
Les cographes sont des graphes de permutation.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Permutation graphe » (voir la liste des auteurs).
- Alain Hertz, « Quelques classes de graphes », sur Centre de recherche inter-universitaire GERAD
- Ben Dushnik et Edwin W. Miller, « Partially ordered sets », American Journal of Mathematics, vol. 63, no 3, , p. 600–610 (DOI 10.2307/2371374, JSTOR 2371374, lire en ligne).
Liens externes
- « Permutation graph », sur Information System on Graph Classes and their Inclusions