Plus petit ancêtre commun

En théorie des graphes, le plus petit ancêtre commun de deux nœuds d'un arbre est le nœud le plus bas dans l'arbre (le plus profond) ayant ces deux nœuds pour descendants. Le terme en anglais est Lowest Common Ancestor (LCA). Les expressions premier ancêtre commun et plus proche ancêtre commun sont aussi utilisées.

Dans cet arbre, le plus petit ancêtre commun de

x

y

est le sommet vert foncé. Les autres ancêtres sont les sommets vert clair.

Divers algorithmes ont été inventés pour trouver rapidement le plus petit ancêtre commun.

Définition

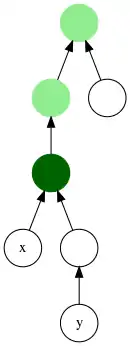
Étant donné un arbre, les ancêtres communs de deux nœuds, sont les sommets qui sont ancêtres de ces deux nœuds ; autrement dit ce sont les nœuds qui ont ces deux nœuds dans leurs descendances. Le plus petit ancêtre commun (PPAC) à ces deux nœuds est l'ancêtre commun le plus profond, c'est-à-dire le plus éloigné de la racine[1].

On peut aussi définir une notion de plus petits ancêtres communs dans un graphe orienté acyclique (DAG).

Algorithmes

Définition et algorithme simple

La plupart des algorithmes qui ont été étudiés pour trouver le PPAC dans un arbre, ont été créés pour répondre à des requêtes pour des couples de nœuds. Ces algorithmes sont donc en deux phases : un preprocessing et un algorithme pour répondre aux requêtes (queries).

Un algorithme simple est de créer une table contenant tous les PPACs, puis de piocher dans ce tableau à chaque requête. Cet algorithme a une complexité en temps de O(n²) (où n est la taille de l'arbre) pour le preproccesing (si l'on utilise la programmation dynamique), et les requêtes sont traitées en temps constant[2].

Algorithmes rapides

De nombreux algorithmes optimaux ont été proposés pour résoudre le problème PPAC. Ces algorithmes sont optimaux en ordre de grandeur, car ils ont une complexité linaire pour le preproccesing et un temps de requête constant.

Certains algorithmes utilisent des structures de données adaptées pour décomposer l'arbre en chemin, alors que d'autres se basent sur un parcours eulérien de l'arbre, et le calcul de range minimum query (en) (parfois appelé minimum d'intervalle[3]).

Variantes

Des algorithmes ont été inventés pour des cas plus généraux, par exemple pour les DAG[4] et pour des modèles plus dynamiques avec ajouts et retraits de nœuds[5].

Applications

Le plus petit ancêtre commun est un objet utilisé notamment en algorithmique du texte et en bio-informatique où de nombreux objets peuvent être représentés par des arbres[6]. Un exemple important est la manipulation des arbres des suffixes, qui permettent de résoudre rapidement certains problèmes comme la recherche de la plus longue sous-chaîne commune[7].

Historique

Le problème qui consiste à trouver le PPAC a été défini la première fois[6] par Aho, Hopcroft et Ullman en 1973[8]. Le premier algorithme optimal est dû à Harel et Tarjan[9], il a ensuite été simplifié par Tarjan et Gabow grâce à la structure Union-Find[10] - [11], puis encore simplifié en 1988[12]. En 1993, Berkman et Vishkin ont publié un algorithme sur un principe complètement différent[13], simplifié en 2000[2].

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Lowest common ancestor » (voir la liste des auteurs).

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction à l'algorithmique, Dunod, 2002 [détail de l’édition], « 21.3. Algorithme différé de Tarjan pour le premier ancêtre commun », p. 508.
Michael A. Bender et Martin Farach-Colton, « The LCA problem revisited », dans Proceedings of the 4th Latin American Symposium on Theoretical Informatics (LATIN), vol. 1776, Springer-Verlag, coll. « Lecture Notes in Computer Science », 2000 (DOI 10.1007/10719839_9, lire en ligne), p. 88-94.
Charles Bouillaguet,Claire Mathieu, « Projet : plus proche ancêtre commun », sur Département informatique ENS, 2014.
Michael A. Bender, Farach-Colton, Giridhar Pemmasani, Steven Skiena et Pavel Sumazin, « Lowest common ancestors in trees and directed acyclic graphs », Journal of Algorithms, vol. 57, n^o 2,‎ 2005, p. 75-94 (lire en ligne).
Richard Cole et Ramesh Hariharan, « Dynamic LCA queries on trees », dans {Proceedings of the tenth annual ACM-SIAM symposium on Discrete algorithms},, 1999, p. 235-244
Johannes Fischer et Volker Heun, « Theoretical and Practical Improvements on the RMQ-Problem, with Applications to LCA and LCE », dans Proceedings of the 17th Annual Symposium on Combinatorial Pattern Matching, vol. 4009, Springer-Verlag, coll. « Lecture Notes in Computer Science », 2006 (DOI 10.1007/11780441_5), p. 36-48
(en) Dan Gusfield, Algorithms on Strings, Trees and Sequences : Computer Science and Computational Biology, Cambridge/New York/Melbourne, Cambridge University Press, 1999, 534 p. (ISBN 0-521-58519-8, lire en ligne)
Alfred Aho, John Hopcroft et Jeffrey Ullman, « On finding lowest common ancestors in trees », dans Proc. 5th ACM Symp. Theory of Computing (STOC), 1973 (DOI 10.1145/800125.804056), p. 253-265.
Dov Harel et Robert E. Tarjan, « Fast algorithms for finding nearest common ancestors », SIAM Journal on Computing, vol. 13, n^o 2,‎ 1984, p. 338-355 (DOI 10.1137/0213024).
Harold N. Gabow et Robert Endre, Tarjan, « A linear-time algorithm for a special case of disjoint set union », dans Proceedings of the fifteenth annual ACM symposium on Theory of computing, 1983, p. 246-251.
Voir Tarjan's off-line lowest common ancestors algorithm (en).
Baruch Schieber et Uzi Vishkin, « On finding lowest common ancestors: simplification and parallelization », SIAM Journal on Computing, vol. 17, n^o 6,‎ 1988, p. 1253-1262 (DOI 10.1137/0217079)
Omer Berkman et Uzi Vishkin, « Recursive Star-Tree Parallel Data Structure », SIAM Journal on Computing, vol. 22, n^o 2,‎ 1993, p. 221-242 (DOI 10.1137/0222017)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.