Graphe de Turán
En théorie des graphes, un graphe de Turán (noté ), aussi appelé maximally saturated graph, est un élément d'une famille de graphes qui portent le nom de Pál Turán.
| graphe de Turán | |
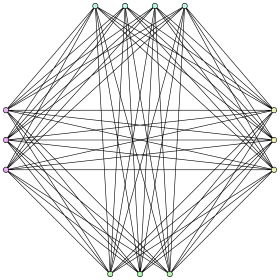 Le graphe de Turan (13,4) | |
| Notation | |
|---|---|
| Nombre de sommets | |
| Nombre d'arêtes | ~ |
| Rayon | |
| Diamètre | |
| Maille | |
| Nombre chromatique | |
Le graphe possède sommets, partitionnés en sous-ensembles les plus équilibrés possibles, et chaque sommet est relié à tous les sommets qui ne sont pas dans son sous-ensemble. Par équilibré, on entend que le graphe a sous-ensembles de taille , et sous-ensembles de taille .
Définition
La graphe the Turán de paramètres n et r, noté possède sommets, partitionnés en sous-ensembles les plus équilibrés possibles, et chaque sommet est relié à tous les sommets qui ne sont pas dans son sous-ensemble. Par équilibré, on entend que le graphe aura sous-ensembles de taille , et sous-ensembles de taille .
Propriétés
Le nombre chromatique du graphe est r[1].
Cas particuliers et inclusions
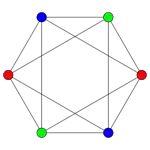
Les graphes bipartis complets sont des graphes de Turán.
Ce sont des cographes, c'est-à-dire qu'ils peuvent être formés par des unions disjointes et des passages au graphe complémentaire. On peut le réaliser de la manière suivante :
pour chaque stable du graphe final,
- faire d'abord une union de tous les sommets,
- passer au complémentaire (dans chaque ensemble) pour avoir des cliques,
- puis faire l'union de toutes les cliques,
- passer encore au complémentaire.
Histoire
Les graphes de Turán portent le nom de Pál Turán, qui les a définis et utilisés pour la démonstration du théorème de Turán[2].
Notes et références
- Chong-Yun Chao et George A Novacky Jr, « On maximally saturated graphs », Discrete Mathematics, Elsevier, vol. 41, no 2, , p. 139-143
- Paul Turán, « On an extremal problem in graph theory », Matematikai és Fizikai Lapok, vol. 48, , p. 436–452










