Graphe de Tietze
Le graphe de Tietze est, en théorie des graphes, un graphe 3-régulier possédant 12 sommets et 18 arêtes. Il est remarquable notamment pour ses propriétés de coloration.
| Graphe de Tietze | |
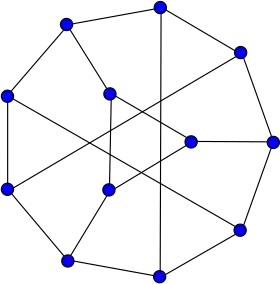 Représentation du graphe de Tietze. | |
| Nombre de sommets | 12 |
|---|---|
| Nombre d'arêtes | 18 |
| Distribution des degrés | 3-régulier |
| Rayon | 3 |
| Diamètre | 3 |
| Maille | 3 |
| Automorphismes | 12 (D6) |
| Nombre chromatique | 3 |
| Indice chromatique | 4 |
| Propriétés | Cubique Snark |
Propriétés générales
Propriétés générales
Le diamètre du graphe de Tietze, l'excentricité maximale de ses sommets, est 3, son rayon, l'excentricité minimale de ses sommets, est 3 et sa maille, la longueur de son plus court cycle, est 3. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.
Coloration
Le nombre chromatique du graphe de Tietze est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 2-coloration valide du graphe.
L'indice chromatique du graphe de Tietze est 4. Il existe donc une 4-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Propriétés algébriques
Le groupe d'automorphismes du graphe de Tietze est un groupe d'ordre 12 isomorphe au groupe diédral D6, le groupe des isométries du plan conservant un hexagone régulier. Ce groupe est constitué de 6 éléments correspondant aux rotations et de 6 autres correspondant aux réflexions.
Le polynôme caractéristique de la matrice d'adjacence du graphe de Tietze est : .
Plongement sur le tore et coloration

Le graphe de Tietze peut être plongé sur un tore. Les faces du graphe ont alors la propriété qu'elles se touchent toutes deux à deux. Ceci a pour conséquence qu'une coloration d'un graphe plongeable sur un tore peut nécessiter six couleurs, ce qui contraste avec le théorème des quatre couleurs dans le cas des graphes planaires[1].
Notes et références
- Heinrich Tietze, « Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen » [« Some remarks on the problem of map coloring on one-sided surfaces »], DMV Annual Report, vol. 19, , p. 155-159 (lire en ligne).
