Front de flamme

Flamme de bougie[1]

Dans le cas typique d'une flamme de bougie (ou de lampe à huile), la « flamme bleue » (zone de la flamme riche en comburant) est approximativement un cône ayant une base de 4 mm de rayon (8 mm de diamètre).

À l'intérieur de ce cône, la « cire » de la bougie (stéarine) fond sous l’effet de la chaleur, progresse dans la mèche, puis se volatilise ; le gaz combustible progresse par diffusion vers le front de flamme où il est consommé.

Le comburant, en général le dioxygène de l'air, se trouve à l'extérieur. Le dioxygène est consommé dans le front de flamme, vers lequel il progresse par diffusion.

Les gaz de combustion chauds, plus légers que l'air, s’élèvent en un courant ascendant, ce qui crée une dépression, à la base de la bougie, qui attire l'air frais, permettant à la combustion de continuer.

La diffusion des molécules obéit aux lois de Fick. Une partie de la chaleur est transportée vers le haut par la convection des gaz chauds, une autre partie se propage horizontalement par conduction thermique, qui obéit à la loi de Fourier. On estime que par diffusion, la vapeur de combustible va à une vitesse d'environ 10 cm/s [2].

Si l'on atteint un régime stationnaire, on peut estimer que l'énergie thermique produite par la flamme est consommée à l'intérieur par la fusion et la vaporisation de la stéarine (chaleurs latentes de fusion et de vaporisation) ; à l'extérieur, la température de la pièce est constante loin de la pièce (la bougie ne suffit pas à réchauffer la pièce).

Flamme de bougie en microgravité.

Dans le cas de la flamme de bougie en microgravité, il n'y a pas de convection. La flamme est hémisphérique. À l'extérieur de l'hémisphère, les gaz chauds produits par la réaction produisent une surpression : d'après la loi des gaz parfaits, la pression augmente avec la température, or là, la température passe de la température ambiante pour les gaz frais (environ 20 °C, soit 293 K) à environ 1 500 °C (1 773 K), la pression est donc multipliée par 6. Cela crée un « vent » qui s'éloigne de la flamme ; cela freine donc la diffusion du comburant.

Lorsque le gaz est au repos dans le référentiel (l'observateur ne voit pas de courant de gaz, pas de vent), on a en général une flamme sphérique, le centre de la sphère étant le point d'inflammation. On peut aussi avoir une flamme sphérique se propageant vers l'intérieur de la sphère : la flamme s'est répandue sur le pourtour de la pièce et se propage vers le centre.

Dans un tuyau, la sphère est « coupée » par les parois et c'est une calotte qui se propage ; au bout d'une certaine distance parcourue, le rayon devient très grand et la calotte paraît plane, avec toutefois une déformation au niveau des parois.

Dans un tuyau, on peut donc estimer que l'on a un front de flamme plan. Ce front de flamme sépare deux zones :

• d'un côté, le gaz frais, prémélange de combustible et de comburant, à température ambiante (environ 20 °C, soit 293 K) ;
• de l'autre côté, les gaz brûlés, à haute température (environ 1 800 °C, soit environ 2 073 K).

Les réactants étant déjà en contact, c'est la propagation de la chaleur qui détermine l'avancée du front de flamme. Celle-ci est donnée par la loi de Fourier.

Si D_T est le coefficient de diffusion thermique et τ est le temps de réaction (l'inverse de la vitesse de réaction), la vitesse du front de flamme u_L est alors :

${\displaystyle u_{\mathrm {L} }\simeq {\sqrt {\frac {\mathrm {D_{T}} }{\tau }}}}$

et l'épaisseur de flamme e vaut

${\displaystyle e\simeq {\sqrt {\tau \cdot \mathrm {D_{T}} }}}$

On a comme ordre de grandeur pour un gaz frais à température ambiante :

• D_T ≃ 0,4 cm²/s ;
• τ ≃ 4 × 10⁻⁴ s ;
• e ≃ 0,13 mm ;
• u_L ≃ 32 cm/s (env. 1 km/h).

(Voir Boyer p. 67 et suiv.) La vitesse de réaction, 1/τ, suit une loi d'Arrhénius, on en déduit que la vitesse du front a la forme

${\displaystyle u_{\mathrm {L} }=u_{0}\cdot \exp \left(-{\frac {\mathrm {E_{A}} }{2k\mathrm {T} }}\right)}$

où E_A est l'énergie d'activation, k est la constante de Boltzmann et T est la température absolue du gaz frais.

Note

Dans toute la section, les notions de vitesse et d'immobilité sont par rapport au référentiel du laboratoire, par rapport à un observateur immobile sur Terre. L'axe des x est orienté des gaz frais vers les gaz brûlés, de la source vers la sortie.

On a fréquemment une alimentation par un flux de gaz.

Considérons le cas d'un tuyau. Si le gaz est immobile, le front de flamme est plan et progresse à une vitesse -u_L.

Si l'on impose un débit de gaz à une vitesse v_g inférieure à u_L,

u_L > v_g,

alors la flamme progresse toujours vers la source, mais plus lentement, à une vitesse -(u_L - v_g).

Si la vitesse du gaz frais est égale à la vitesse de la flamme

u_L = v_g

alors la flamme reste immobile dans le tuyau. Ce cas est intéressant car d'une part il permet d'étudier simplement le front de flamme, puisqu'il est immobile, et d'autre part il permet de calculer simplement la vitesse d'éjection des gaz brûlés. En effet, il ne peut y avoir d'accumulation de gaz dans le tuyau ; pendant un temps t, la réaction consomme un volume u_L⋅S₀⋅t, et produit un volume k fois plus important de gaz ; k vaut 6[3] ou plus. La vitesse d'éjection est donc

${\displaystyle v_{e}=k\cdot u_{L}}$

donc les gaz s'éjectent à une vitesse au moins 6 fois plus élevée que la vitesse de front, de l'ordre de 200 cm/s (env. 7 km/h).

Si la vitesse du gaz frais est supérieure à la vitesse de la flamme

u_L < v_g,

alors la flamme progresse vers la sortie. Pour des vitesses modérées, on a une flamme conique qui reste « accrochée » à la sortie.

En effet, dans le cas d'un écoulement dans une tuyauterie, le gaz est soumis à un frottement fluide avec les parois, la vitesse est donc plus lente au bord qu'au centre. Il y a donc un endroit auquel la vitesse du fluide est égal à la vitesse de flamme ; la flamme reste donc immobile à cet endroit là et empêche que la flamme soit soufflée.

La forme conique est donc due à un gradient de vitesse du gaz frais entre le centre du tuyau et le bord, soumis à un frottement fluide. Il ne s'agit pas d'un cône parfait, mais nous allons faire cette hypothèse simplificatrice.

Dans le cas de la flamme plane immobile (u_L = v_g), le front de flamme a pour surface la section du tuyau, S₀. La consommation de gaz frais par la combustion est égale au débit de gaz

${\displaystyle \mathrm {D} =v_{\mathrm {g} }\cdot \mathrm {S} _{0}=u_{\mathrm {L} }\cdot \mathrm {S} }$.

La flamme conique a elle une surface plus importante. Si α est le demi-angle au sommet, alors la surface S du front de flamme vaut (cf. Cône (géométrie) > Cas du cône de révolution) :

${\displaystyle \mathrm {S} ={\frac {\mathrm {S} _{0}}{\sin \alpha }}}$

La consommation de gaz vaut u_L⋅S (la vitesse du front de flamme reste inchangée), et elle doit être égale au débit :

${\displaystyle \mathrm {D} =u_{\mathrm {L} }\cdot \mathrm {S} =v_{\mathrm {g} }\cdot \mathrm {S} _{0}}$

soit

${\displaystyle u_{\mathrm {L} }\cdot {\frac {\mathrm {S} _{0}}{\sin \alpha }}=v_{\mathrm {g} }\cdot \mathrm {S} _{0}}$

et donc

${\displaystyle \sin \alpha ={\frac {u_{\mathrm {L} }}{v_{\mathrm {g} }}}}$

on retrouve bien là le fait que plus le débit est important, plus la flamme est effilée. L'augmentation du débit est compensée par un étirement de la flamme, qui augmente la surface du front, qui provoque une augmentation de la consommation donc de la puissance thermique.

Alors que le flux de gaz frais est dans l'axe du tube, les gaz brûlés s'échappent « en diagonale ». En effet, si l'on considère un front plan, les gaz s'échappent perpendiculairement à ce plan ; ici, leur vitesse est la composée de la vitesse initiale du gaz frais et de la vitesse d'échappement perpendiculaire à la surface du cône. Puis, leur trajectoire s'incurve pour devenir verticale (ils montent par poussée d'Archimède)

Turbulences créées par un obstacle

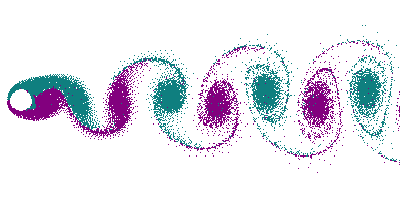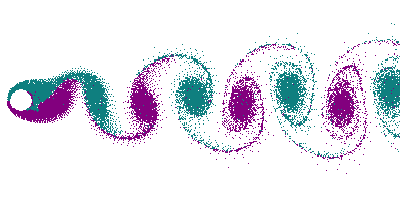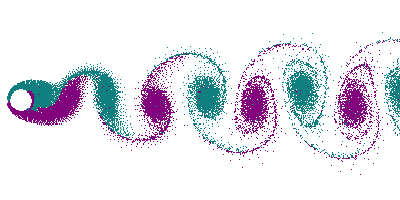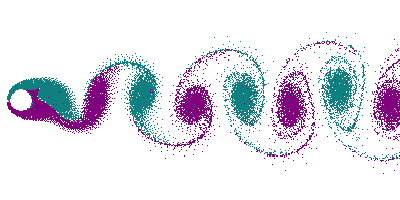
Dans le cas d'un écoulement turbulent, les turbulences vont déformer le front de flamme. En particulier, les tourbillons (vortex) créés par un obstacle (allée de Bénard-Von Karman) vont déformer le front en le traversant, donnant naissance à un front « plissé ». Dans le cas extrême de grands tourbillons, on peut avoir un front de flamme qui s'enroule dans le tourbillon, offrant ainsi une très grande surface.

Le plissement augmente la surface du front de flamme, et comme dans le cas d'une flamme conique, cela se traduit par une augmentation de la consommation de gaz, donc par une augmentation de la puissance thermique.

Dans un souci de compacité du brûleur, de la chaudière, du réacteur, on a donc intérêt à avoir un écoulement le plus turbulent possible, afin d'avoir la plus grande surface de front de flamme pour un volume donné (voir Surface spécifique). Ceci permet d'augmenter le rapport puissance/volume, et puissance poids, capital dans le cas de l'aéronautique.

En outre, la présence d'un obstacle dans le flux va provoquer un ralentissement du flux en amont, et donc constituer un accroche-flamme.

Les turbulences sont créées par le frottement du gaz sur les parois et obstacles. La présence de turbulences est donc conditionnée par la vitesse du fluide et par sa viscosité, sa capacité à transmettre les variations de vitesse. Elles apparaissent lorsque le nombre de Reynolds R_e est élevé, c'est-à-dire lorsque la vitesse est élevée. C'est donc là encore l'augmentation du débit qui provoque l'augmentation de la puissance.