Formule du nivellement barométrique
La formule du nivellement barométrique décrit la répartition verticale des molécules de gaz dans l'atmosphère de la Terre, et donc la variation de la pression atmosphérique en fonction de l'altitude.
On parle ainsi d'un gradient vertical de pression, mais qui ne peut être décrit mathématiquement qu'en approximations, en raison de la dynamique de la météorologie dans l'atmosphère inférieure. En première approximation, on peut supposer que près du niveau de la mer, la pression diminue d'un hectopascal quand l'altitude augmente de 8 mètres.
Équation hydrostatique
La variation de la pression et de la masse volumique de l'air dans l'atmosphère est décrite par l'équation de la statique des fluides.

Pour l'établir, considérons un volume élémentaire de surface de base A et de hauteur infinitésimale dh, contenant de l'air de masse volumique ρ. Le poids dP de ce volume d'air est donné par .
En dessous du volume s'exerce une force vers le haut due à la pression atmosphérique p. La force exercée vers le bas par la pression atmosphérique sur le dessus du volume est .
Nous n'avons pas besoin de considérer les forces de pression qui s'exercent sur les côtés du volume élémentaire, car elles s'équilibrent.
A l'équilibre hydrostatique, la somme vectorielle des forces qui s'exercent sur le volume élémentaire est nulle :
soit .
On obtient donc la relation : .
D'après la loi des gaz parfaits, la masse volumique de l'air s'écrit : . Ainsi :|
|
M est la masse molaire moyenne des gaz de l'atmosphère (0,028 964 4 kg/mol), g l'accélération de la pesanteur (9,806 65 m/s2), R la constante universelle des gaz parfaits (8,314 462 618 15 J K−1 mol−1) et T la température absolue (K).
L'équation hydrostatique décrit de quelle quantité dp la pression atmosphérique varie pour une petite variation dh de l'altitude. Comme le montre la présence du signe moins, dp est négatif quand dh est positif : la pression diminue quand l'altitude augmente. Par exemple, à une pression moyenne de p = 1 013 hPa au niveau de la mer et pour une température de 288 K (15 °C), la pression diminue de 0,12 hPa lorsque l'altitude augmente de 1 m, et de 1 hPa quand l'altitude augmente de 8,3 m. On appellera échelon barométrique la différence d'altitude pour laquelle la différence de pression est de 1 hPa. Pour des altitudes et des températures plus importantes, la pression varie moins vite et l'échelon barométrique augmente.
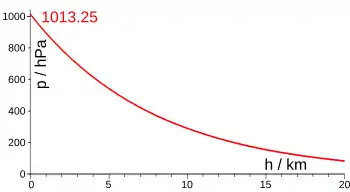
De manière générale, on souhaite obtenir des valeurs explicites de la pression ou de la masse volumique en fonction de l'altitude. On peut obtenir les variations de pression pour de grandes variations d'altitude en utilisant la méthode de séparation des variables : puis en intégrant l'équation barométrique : .
L'intégration du terme de gauche donne . Pour intégrer le terme de droite, il nous faut connaître la dépendance à l'altitude de T et g. L'accélération de la pesanteur peut être considérée comme constante pour des altitudes raisonnables. En revanche, T varie de manière complexe et imprévisible en fonction de l'altitude. Il est donc nécessaire d'émettre des hypothèses simplificatrices sur l'évolution de T en fonction de l'altitude h.
Atmosphère isotherme
La formule du nivellement barométrique pour l'atmosphère isotherme est l'hypothèse la plus souvent citée dans les cours ou la littérature introductive. La température T est uniforme quelle que soit l'altitude.
Établissement à partir de l'équation barométrique
Pour T constant, l'intégration de l'équation barométrique donne :
Pour T constant, et en introduisant l'altitude caractéristique , on simplifie l'équation en :
|
|
À chaque augmentation de l'altitude de hs, la pression diminue d'un facteur . L'altitude caractéristique est ainsi une mesure naturelle pour la hauteur de l'atmosphère et de l'évolution de la pression en son sein. Pour ce modèle d'atmosphère, elle vaut environ 8,4 km pour T = 15 °C.
La masse volumique s'exprime de manière similaire :
|
|
Pour un observateur descendant une montagne, la pression augmente continûment, puisqu'une colonne d'air de plus en plus lourde repose sur lui.
Ici l'augmentation est exponentielle, car l'air est compressible : pour chaque mètre de variation d'altitude, le poids d'une colonne d'air reposant sur une certaine surface augmente du poids du volume de la colonne d'air qui s'y ajoute. Ce poids dépend de la densité de l'air, qui dépend elle-même de la pression. La pression augmente donc d'autant plus vite qu'elle est déjà importante. (Si une grandeur varie d'une valeur proportionnelle à cette grandeur, la variation globale sera exponentielle.)
Établissement à partir de la physique statistique
Considérons un système de particules à l'équilibre thermique à la température T (qui a donc la même température en tout point) dont les particules peuvent occuper des niveaux d'énergie Ej répartis discrètement ou continûment.
La probabilité qu'une particule occupe le niveau d'énergie Ej est donnée par la distribution de Boltzmann :
- .
kb est la constante de Boltzmann et Z un facteur de normalisation (la fonction de partition) qui assure que la somme sur toutes les probabilités est égale à 1. Pour un système constitué de N particules, le nombre de particules dans l'état Ej est nj = N Pj.
Une particule de gaz de masse m a dans le champ de pesanteur une énergie potentielle Epot=mgh et, à cause de sa température dans le milieu, une énergie thermique Eth; donc au total, une énergie E(h)=mgh+Eth. Si l'on considère deux volumes élémentaires de même taille à des altitudes h0 et h1, les particules à l'altitude h1 ont une énergie supérieure de mgΔh. Le rapport des probabilités de présence d'une particule dans le volume à h1 et dans le volume à h0 vaut donc :
- .
Pour un nombre de particules N suffisamment grand, la densité de particules n(h) se comporte comme les probabilités de présence :
- ,
et d'après la loi des gaz parfaits , la pression obéit à la même relation :
Du point de vue énergétique, on a supposé ici les hypothèses du théorème d'équipartition vérifiées. Mais cette hypothèse n'est en général vérifiée que pour une atmosphère dense, seul cas où les énergies entre les différents degrés de liberté peuvent être échangés par chocs entre les molécules de gaz.
(Justification : Le théorème d'équipartition n'est en général valable que pour les hautes énergies car il ne peut être utilisé directement que sur des potentiels de forme quadratiques dans la fonction de Hamilton. Comme l'énergie potentielle d'altitude n'est que linéaire dans la fonction de Hamilton, on ne peut en général pas supposer le théorème d'équipartition valide pour les gaz très dilués.)
Atmosphère adiabatique
D'après l'équation barométrique et pour une transformation adiabatique telle que , on a :
Une solution est :
En introduisant le facteur , on a pour la pression, la masse volumique et la température :
La variation de température est linéaire.
En considérant :
- l'exposant adiabatique de l'air sec κ = 1,402,
- l'accélération de la pesanteur g = 9,807 m s−2,
- la masse volumique ρ0 = 1,23 kg m−3,
- la pression p0 = 1,013 bar
- la température à T0 = 288 K l'altitude h0
on a :
et le gradient de température vaut :
C'est environ le gradient de température indiqué dans la section suivante, qui lui est en revanche déterminé à partir de l'expansion adiabatique de l'air humide : l'exposant adiabatique de l'air humide est plus faible que l'exposant adiabatique de l'air sec, et donc h0 croît.
D'autres limitations de l'hypothèse adiabatique :
- Si l'air devient très froid, l'exposant adiabatique de l'air sec varie également.
- À de très grandes altitudes (densité faible), le libre parcours moyen devient très grand, et les équations ne sont plus valables.
- En outre, l'effet de serre invalide l'hypothèse adiabatique selon laquelle il n'y a pas d'échanges énergétiques avec l'environnement.
Atmosphère avec évolution de température linéaire
Établissement
Dans le cas général, la température n'est pas constante mais varie avec l'altitude. L'hypothèse la plus simple pour tenir compte de cette variation est de supposer une diminution linéaire de la température avec l'altitude. Ainsi pour la température T(h) :
- ,
où a est la valeur (positive) du gradient de température vertical, qui indique de combien de kelvins la température diminue par mètre de différence d'altitude.
L'intégration du terme de droite de l'équation barométrique donne :
- .
Comme
le calcul de l'intégrale donne
- ,
donc finalement, l'intégration de l'équation barométrique
donne :
- ,
La formule du nivellement barométrique pour une variation linéaire de la température devient :
|
|
Et pour la masse volumique :
|
|
L'exposant est diminué de 1 car le rapport entre pression et masse volumique dépend de la température.
En aéronautique, cette formule du nivellement barométrique "étendue" est à la base de la fonction du nivellement barométrique pour l'atmosphère standard, où l'atmosphère est discrétisée en couches élémentaires avec interpolation linéaire de l'évolution de la température. En commençant par la couche la plus basse, la température et la pression à la frontière haute d'une couche élémentaire sont calculées, et utilisées comme données pour la frontière basse de la couche suivante. Ainsi, on construit de manière inductive le modèle de l'atmosphère tout entière.
Gradients de température typiques
Comme le montrent des mesures des profils de température dans l'atmosphère, l'hypothèse de l'évolution linéaire de la température est une bonne approximation, même s'il apparaît dans certains cas des déviations importantes (en particulier lors d'inversions météorologiques).
L'origine principale de cette diminution de la température avec l'altitude est que les couches basses de l'atmosphère sont chauffées par la surface de la Terre (elle-même chauffée par le soleil), tandis que les couches hautes rayonnent de la chaleur vers l'espace. À ceci s'ajoutent des variations de température adiabatiques sèches ou humides de paquets d'air ascendants ou descendants, et d'autres modifications dues au mélange de masses d'air d'origines différentes.
Dans des masses d'air chaud, le gradient de température prend des valeurs de 0,3 à 0,5 K pour 100 m, des valeurs de 0,6 à 0,8 K pour 100 m dans l'air froid, et 0,65 K pour 100 m en moyenne. Dans des zones de vallées, des inversions météorologiques régulières peuvent faire baisser le gradient de température jusqu'à 0,5 K pour 100 m, voire à 0,4 K pour 100 m durant les mois d'hiver.
On se limitera à la description des variations de température et de pression dans la troposphère. Dans la stratosphère, la température diminue moins vite, voire augmente à nouveau par l'absorption de rayons UV dans la couche d'ozone.
Pour un gradient de température de 0,65 K pour 100 m, l'exposant Mg/Ra prend la valeur numérique approchée de 5,25578595912636987 (avec les valeurs numériques exactes de M=0,0289644, g=9,80665 et R=8,31446261815), résultat qui est arrondi — de façon erronée — à 5,255 (au lieu de 5,256) :
Sous cette forme (et en prenant dans la suite des calculs l'exposant arrondi à 5,255, et non pas à 5,256), on peut utiliser la formule de nivellement dans le cas courant où l'on connaît la température et la pression à une des deux altitudes, mais pas le gradient de température.
| Altitude en m |
Pression en hPa |
Baisse en % |
|---|---|---|
| 0 m | 1013,25 | 0 |
| 500 m | 954,61 | 5,78 |
| 1 000 m | 898,76 | 11,30 |
| 1 500 m | 845,58 | 16,55 |
| 2 000 m | 794,98 | 21,54 |
| 2 500 m | 746,86 | 26,29 |
| 3 000 m | 701,12 | 30,80 |
| 3 500 m | 657,68 | 35,09 |
| 4 000 m | 616,45 | 39,16 |
| 4 500 m | 577,33 | 43,02 |
| 5 000 m | 540,25 | 46,68 |
| 6 000 m | 471,87 | 53,43 |
| 7 000 m | 410,66 | 59,47 |
| 8 000 m | 356,06 | 64,86 |
| 9 000 m | 307,48 | 69,65 |
| 10 000 m | 264,42 | 73,90 |
| 11 000 m | 226,37 | 77,66 |
On obtient également le tableau suivant pour la dépendance à l'altitude et à la température de l'échelon de nivellement barométrique :
| échelon de nivellement barométrique [m/hPa] | ||||
|---|---|---|---|---|
| h | −15 °C | 0 °C | 15 °C | 30 °C |
| 0 m | 7,5 | 7,9 | 8,3 | 8,8 |
| 500 m | 7,9 | 8,3 | 8,7 | 9,2 |
| 1 000 m | 8,3 | 8,7 | 9,2 | 9,6 |
| 2 000 m | 9,3 | 9,7 | 10,1 | 10,6 |
| 3 000 m | 10,4 | 10,8 | 11,2 | 11,6 |
Pour des altitudes et des températures moyennes, on utilise souvent la formule « 1 hPa / 30ft ». Cette approximation est souvent utilisée par les pilotes pour des calculs mentaux rapides.
Formule internationale du nivellement barométrique
En prenant le niveau de la mer comme altitude de référence h0, et en prenant pour l'atmosphère un état moyen défini par l'atmosphère normalisée type OACI (Température 15 °C = 288,15 K, pression 1013,25 hPa, gradient vertical de température 0,65 K pour 100 m), on obtient la formule internationale du nivellement barométrique :
Cette formule permet le calcul de la pression à une certaine altitude, sans avoir besoin de connaître la température ou le gradient vertical de température. La précision dans le cas d'applications pratiques est toutefois limitée, puisque l'on choisit ici un état moyen différent de l'état réel de l'atmosphère.
Cas général
Dans le cas général, la solution de l'équation barométrique est :
- ,
soit
avec une intégrale restant à calculer.
Température virtuelle
La constante des gaz parfaits R est une constante universelle et peut être sortie de l'intégrale. La masse molaire moyenne des gaz de l'atmosphère M est, sauf en cas de très fortes variations de l'humidité de l'air, pratiquement constante au sein de la troposphère et peut également être sortie de l'intégrale. Dans une atmosphère au repos, les différences d'altitude caractéristique hs entre les différents gaz de l'atmosphère, qui ont des masses molaires différentes, pourraient conduire à une séparation des gaz, les gaz les plus légers se concentrant dans les couches supérieures et les gaz lourds dans les couches inférieures. Mais ce n'est pas le cas grâce à un mélange important des gaz dû aux conditions météorologiques dans la troposphère. La variation de l'humidité de l'air ainsi que d'autres causes de variation de M peuvent être prises en compte en considérant la température virtuelle correspondante Tv au lieu de la température réelle T. On peut ainsi utiliser pour M la valeur de la masse molaire de l'air sec au niveau de la mer.
Altitude géopotentielle
La diminution de l'accélération de la pesanteur g avec l'altitude doit être prise en compte en cas de grandes altitudes ou d'exigences de précision importantes. Une accélération de la pesanteur variable dans l'intégrande de la solution de l'équation barométrique complique énormément le problème. Pour le contourner, on utilise la notion d'altitude géopotentielle plutôt que l'altitude géométrique. Imaginons une masse m soulevée du niveau de la mer jusqu'à une altitude h, avec g variable. Comme g diminue avec l'altitude, l'énergie potentielle ΔEpot gagnée par la masse est inférieure à l'énergie potentielle pour g = g0. L'altitude géopotentielle hp est l'altitude à laquelle soulever la masse m à g = g0 constant pour lui apporter la même énergie potentielle ΔEpot. (En d'autres termes, hp est le potentiel gravitationnel divisé par g0.) L'altitude géopotentielle est mesurée en mètre géopotentiel; les surfaces de même altitude géopotentielle sont des surfaces équipotentielles dans le champ de pesanteur.
Pour l'altitude géopotentielle hp correspondant à une altitude géométrique h, on a :
- ,
d'où
- .
En ce qui concerne le rapport entre l'accélération de la pesanteur à l'altitude h et l'accélération de la pesanteur g0, le champ de gravitation diminue quadratiquement en fonction de la distance au centre de la Terre :
- .
vaut 6 356 km (rayon de la Terre). Il faut aussi prendre en compte le fait que l'accélération de la pesanteur au niveau de la mer g0 dépend de la latitude.
De cette manière, il faut convertir les altitudes géométriques en altitudes géopotentielles avant le calcul, ce qui permet d'utiliser l'accélération de la pesanteur au niveau de la mer g0 dans les calculs plutôt qu'une accélération de la pesanteur variable. Pour de faibles altitudes, la différence entre altitudes géométrique et géopotentielle est assez faible et souvent négligeable :
| géométrique | géopotentiel |
|---|---|
| 0 m | 0,0 m |
| 500 m | 500,0 m |
| 1 000 m | 999,8 m |
| 5 000 m | 4 996,1 m |
| 10 000 m | 9 984,3 m |
En utilisant l'accélération de la pesanteur au niveau de la mer g0, les altitudes géopotentielles hp0 et hp1 et la température virtuelle Tv, la formule du nivellement barométrique générale se simplifie en :
- .
Il reste à calculer l'intégrale de 1/Tv, ce qui suppose de connaître le profil de température Tv(hp). Il peut par exemple être déterminé à l'aide de radiosondes. Pour des modèles simplifiés d'atmosphère à température constante ou d'évolution linéaire, on retrouve les formules de nivellement traitées au début.
Applications
Théorie
La pression de l'air mesurée par un baromètre dépend de l'état météorologique de l'atmosphère mais également de l'altitude de mesure. Si l'on a besoin de comparer les mesures de différents baromètres en différents lieux (par exemple pour estimer l'état d'une dépression ou d'un front), il faut s'affranchir de l'influence de l'altitude de mesure sur les données relevées. Dans ce but, les pressions mesurées sont rapportées à une altitude de référence, en général le niveau de la mer, à l'aide d'une formule de nivellement. Ce calcul est appelé réduction (même si les valeurs augmentent). Le résultat de cette réduction est la pression réduite au niveau de la mer (ou PNM).
Il faut utiliser la bonne formule suivant chaque exigences de précision. Pour un calcul approché, on peut calculer un facteur de réduction à partir de la formule de nivellement à température constante (pour laquelle il faut néanmoins choisir une température représentative) :
Pour une altitude standard de 500 m et en choisissant une température annuelle moyenne de 6 °C, on trouve un facteur de réduction de 1,063. Les valeurs mesurées seront à multiplier par ce facteur.
Si l'on a besoin de plus de précision, il faut au moins prendre en compte la température réelle de l'air. On peut voir son influence sur l'exemple suivant, où l'on a mesuré une pression de 954,3 hPa à une altitude de 500 m, en utilisant la formule de nivellement barométrique pour une évolution de température linéaire (a=0,0065 K/m) en fonction de différentes températures T(h). La réduction donne :
| T(h) | −10 °C | 0 °C | 10 °C | 20 °C | 30 °C |
|---|---|---|---|---|---|
| p0 | 1017,9 | 1015,5 | 1013,3 | 1011,2 | 1009,3 |
On voit que le choix de la température se traduit par des différences de pression de l'ordre du hPa. Si l'on souhaite obtenir une bonne précision, que les profils de température sont disponibles, et que la précision et l’étalonnage du baromètre utilisé justifient les moyens, la réduction devrait toujours se faire avec les profils de température réels. On peut alors utiliser la formule de nivellement correspondant à une évolution linéaire de la température. On pourrait également utiliser la variante à température constante, en utilisant la température à mi-hauteur :
Cette variante est en théorie un peu moins précise, puisqu'elle ne prend pas en compte la variation de la température avec l'altitude, alors que la variante linéaire la prend en compte par hypothèse. Toutefois, pour les températures et altitudes utilisées dans les stations météorologiques, la différence est négligeable.
La formule de réduction recommandée par le service météorologique allemand correspond à la variante à température constante. La température à mi-hauteur est estimée à partir de la mesure de la température à l'altitude de mesure, à l'aide du gradient de température standard. L'humidité de l'air est prise en compte par l'utilisation de la température virtuelle correspondante.
avec
| Pression réduite au niveau de la mer | ||
| Pression à l'altitude du baromètre (en hPa, précision de 0,1 hPa) | ||
| = 9,806 65 m/s2 | Accélération de la pesanteur standard | |
| = 287,05 m2/(s2 K) | Constante spécifique de l'air sec (= R/M) | |
| Altitude du baromètre (en m, à 1 dm près ; on peut effectuer les calculs à partir de l'altitude géométrique jusqu'à 750 m, au-delà il faut utiliser l'altitude géopotentielle) | ||
| Température de mesure (en K, avec T(h) = t(h) + 273,15 K) | ||
| Température de mesure (en °C) | ||
| = 0,0065 K/m | Gradient de température vertical | |
| Pression partielle de vapeur d'eau (en hPa) | ||
| = 0,12 K/hPa | Coefficient correctif pour la pression partielle, pour prendre en compte de la variation moyenne de la pression partielle de vapeur en fonction de l'altitude (dépendant du lieu de mesure, mais supposé constant ici) |
Si l'on ne dispose pas de mesure de l'humidité de l'air, on peut estimer E avec les approximations suivantes, basées sur des moyennes annuelles de la température et de l'humidité :
Pratique

Pour un météorologue amateur, les exigences de précision pour la mesure de la pression et de l'altitude du baromètre décrites précédemment n'ont en général pas besoin d'être satisfaites. Pour un baromètre de station météorologique amateur, il faut compter sur une erreur systématique d'au moins 1 à 2 hPa. Une telle incertitude correspond à une incertitude sur l'échelon barométrique de 10 à 20 m. Vouloir estimer plus précisément l'altitude de mesure ne conduirait probablement pas à une meilleure précision. Dans cette optique, il faudrait déjà estimer s'il est pertinent ou non de considérer l'influence de l'humidité de l'air.
Il ne faut pas utiliser l'altitude réelle, mais l'altitude fictive qui correspond à la meilleure approximation de la pression réduite au niveau de la mer, à partir des données d'un baromètre de référence proche (station météorologique officielle, aéroport, etc.). Avec un étalonnage de ce type, on peut compenser en grande partie l'erreur systématique du baromètre. Il est approprié d'utiliser une altitude approchée pour la réduction, puis de comparer ses propres mesures avec une mesure de référence sur une certaine durée et pour différentes températures. Si l'on remarque une erreur systématique, on peut calculer la différence d'altitude avec la bonne formule de nivellement afin de modifier l'altitude réduite en conséquence. Si l'on ne considère pas l'impact de la température, il faut effectuer l’étalonnage pour une température représentative.

Les baromètres de salon sont en général réglés pour indiquer la pression réduite à l'aide d'une vis à l'arrière de l'objet, qui permet de régler la tension du ressort de la capsule de Vidie. Cet étalonnage correspond donc à un décalage de la graduation. En théorie, c'est un étalonnage incorrect : comme le montrent les formules de nivellement, la réduction au niveau de la mer se fait par une multiplication par un facteur d’étalonnage, et non une simple addition de constante (la pression réduite au niveau de la mer varie d'un peu plus qu'un hPa quand la pression à l'altitude du baromètre varie de 1 hPa). L'échelle de graduation doit donc être légèrement étirée en plus d'être décalée. L'erreur correspondante est toutefois plus faible que l'erreur provenant de la non prise en compte de l'influence de la température. Comme il n'est pas possible d'indiquer au baromètre l'altitude actuelle, l’étalonnage ne peut se faire que par comparaison avec un baromètre de référence. L’étalonnage doit se faire à l'altitude du baromètre (ou bien à un endroit de même altitude) : cela n'a pas de sens de faire étalonner « correctement » l'appareil chez son fabricant ou vendeur s'il celui-ci est situé à un tout autre endroit. Lorsque le baromètre est utilisé pour une prévision météorologique à court terme par la mesure des variations de pression, un étalonnage exact n'est pas aussi nécessaire.
Limites
En général, lors de la réduction de mesures de pression, il faut être conscient que la colonne d'air ajoutée par calcul ne peut souvent pas exister réellement et ne donne pas la « vraie » valeur de la « pression réduite niveau de la mer »…
Les formules de réduction reposent sur des conventions et servent, au-delà d'applications scientifiques spécifiques, à rendre les mesures de stations météorologiques différentes aussi comparables que possible.
Un exemple de la fictivité de la colonne d'air ajoutée : sur une plaine sur laquelle ne s'écoule pas d'air froid, l'air près du sol peut se refroidir par une nuit claire à cause du rayonnement thermique du sol (phénomène d'inversion). Une station météorologique à cet endroit enregistrerait cette température moindre. Si cette plaine s'était trouvée au niveau de la mer, l'air ne se serait pas refroidi (absence du sol responsable de l'inversion), et la colonne d'air réelle aurait eu une température bien plus importante que la colonne d'air calculée. Le calcul a admis une trop grande densité de l'air de la colonne d'air, et donne une pression réduite plus importante que la pression réelle au niveau de la mer.
Mesures d'altitudes
La dépendance de la pression atmosphérique à l'altitude permet de calculer des hauteurs. De telles mesures de hauteur sont rapides et simples à mettre en œuvre, mais leur précision est limitée. Un baromètre utilisé pour la mesure d'altitude est appelé altimètre. Les méthodes de mesures dépendent de l'utilisation et des exigences de précision. Ce genre de mesures servent entre autres pour les randonnées, ou bien pour la topographie dans le cas de mesures plus précises.
Articles connexes
Source
- (de) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en allemand intitulé « Barometrische Höhenformel » (voir la liste des auteurs).







































































