Expérience d'Aspect
En mécanique quantique, l'expérience d'Aspect est la première expérience montrant la violation des inégalités de Bell, établissant un résultat irréfutable en vue de la validation du phénomène d'intrication quantique et des hypothèses de non-localité. Elle apporte ainsi une réponse expérimentale au paradoxe EPR proposé une cinquantaine d'années plus tôt par Albert Einstein, Boris Podolsky et Nathan Rosen.
Cette expérience a été réalisée par le physicien français Alain Aspect à l'Institut d'Optique à Orsay entre 1980 et 1982. Il a reçu pour cela le prix Nobel de physique en 2022. Son importance a été immédiatement reconnue par la communauté scientifique, valant même à cette expérience la couverture du magazine de vulgarisation Scientific American. Bien que la méthodologie mise en œuvre présente une faille potentielle, l'échappatoire de détection, le résultat est jugé décisif et donne lieu par la suite à de nombreuses autres expériences confirmant l'expérience originelle[1].
Contexte scientifique et historique
Avant de parler de l'expérience en elle-même, et afin de bien la comprendre, il est nécessaire de la replacer dans le contexte historique et scientifique qui a amené à sa réalisation.
Intrication quantique
L'intrication quantique est un phénomène qui a été pour la première fois théorisé par Erwin Schrödinger en 1935[2].
La mécanique quantique stipule que deux systèmes quantiques différents (deux particules par exemple) ayant interagi, ou ayant une origine commune, ne peuvent pas être considérés comme deux systèmes indépendants. Dans le formalisme quantique, si le premier système possède un état et le second un état , alors le système intriqué résultant est représenté par une superposition quantique du produit tensoriel de ces deux états : . Dans cette notation, il apparaît nettement que l'éloignement physique des deux systèmes ne joue aucun rôle dans l'état d'intrication (car il n'apparaît aucune variable de position). L'état quantique intriqué reste identique — toutes choses étant égales par ailleurs — quel que soit l'éloignement des deux systèmes.
Par conséquent, si une opération de mesure est effectuée sur ce système quantique intriqué, alors cette opération est valable pour les deux systèmes composant l'intricat : les résultats des mesures des deux systèmes sont corrélés.
Paradoxe EPR
Ce résultat a profondément choqué Albert Einstein qui avait une vision réaliste locale de la physique. Cette vision mène à la conclusion que si l'acte de mesure influe sur les deux systèmes, il existerait alors une influence se propageant d'un système à l'autre, à une vitesse non limitée par celle de la lumière. Le formalisme quantique prévoit que l'influence de l'acte de mesure sur les deux composantes d'un système intriqué a un effet instantané sur ses deux composantes, quel que soit leur éloignement.
Toujours en 1935, Albert Einstein, Boris Podolsky, et Nathan Rosen (E.P.R.) ont alors imaginé une expérience de pensée qui, si on estimait que les états intriqués existent réellement, mène à un paradoxe : soit une influence se déplace plus vite que la lumière (non-causalité), soit la physique quantique est incomplète. Aucun des deux termes de l'alternative n'était acceptable à l'époque, d'où le paradoxe.
Ce paradoxe était d'une grande importance historique, mais n'a pas eu de retentissement immédiat. Seul Niels Bohr a pris au sérieux l'objection apportée par ce paradoxe, et a tenté d'y répondre. Mais cette réponse était d'ordre qualitatif, et rien ne permettait de trancher de manière indubitable entre les deux points de vue. Ainsi, la réalité de l'intrication restait alors une question de point de vue sans support expérimental direct, l'expérience EPR n'étant pas réalisable (à cette époque) en pratique.
En effet, deux obstacles majeurs s'opposaient à la réalisation de cette expérience : d'une part les moyens techniques de l'époque étaient insuffisants, mais aussi (et surtout) il n'y avait apparemment aucun moyen de mesurer directement (par des critères quantitatifs) les effets EPR.
Remarquons que cette simultanéité, quel que soit le sens qu'on lui donne[3], ne pourra être constatée que par la comparaison des deux mesures distantes, elle-même limitée par la vitesse de la lumière. Elle ne peut avoir une influence causale, ou - ce qui revient au même - transmettre une information, rendant cette propriété compatible avec la théorie de la relativité selon laquelle aucune information ne peut se propager à une vitesse superluminique.
Inégalités de Bell
Les choses sont restées à peu près en l'état jusqu'en 1964. Le physicien irlandais John Stewart Bell publia alors un article dans lequel il mit en évidence des effets quantitatifs et mesurables des expériences de type EPR. Ce sont les fameuses inégalités de Bell. Ces inégalités sont des relations quantitatives que doivent vérifier les corrélations de mesures entre systèmes qui respectent totalement la causalité relativiste. Si ces inégalités sont violées, alors il faut admettre des influences instantanées à distance.
Ces inégalités permettaient de lever un des deux obstacles à la réalisation d'expériences EPR. Mais en 1964, les moyens techniques étaient toujours insuffisants pour mettre en place concrètement ce type d'expérience.
Premières expériences de test des inégalités de Bell
La réalisation d'expériences EPR a commencé à être techniquement envisageable à partir de 1969, un article ayant été publié montrant la faisabilité d'une expérience[4].
Deux universités, Harvard et Berkeley, ont commencé à mettre en œuvre un protocole expérimental sur ces bases, et les expériences ont eu lieu en 1972. Les résultats furent contradictoires : Harvard constata une vérification des inégalités de Bell, et par conséquent une contradiction avec les prédictions de la physique quantique. Berkeley trouva au contraire une violation des inégalités de Bell, et une vérification de la physique quantique.
Le problème avec ces expériences était notamment une source de particules intriquées peu fiable et à faible débit, ce qui nécessitait des temps d'expériences s'étendant sur plusieurs jours en continu. Or, il est excessivement difficile de maintenir des conditions expérimentales constantes et maîtrisées sur un temps aussi long, surtout avec des expériences aussi délicates. Les résultats des deux expériences étaient donc sujets à caution.
En 1976, la même expérience fut répétée à Houston avec une meilleure source de photons intriqués, de débit plus élevé. Cela permettait de descendre le temps de l'expérience à 80 minutes. Mais en contrepartie, les photons n'étaient pas polarisés de manière optimale pour faire apparaître clairement les violations des inégalités de Bell. Néanmoins, cette expérience montra une violation des inégalités de Bell. Mais celle-ci était faible, et le doute était encore permis.
Mais aussi — et surtout en fait — ces expériences n'étaient pas assez élaborées pour évacuer la possibilité de corrélations (qui entraînent une violation des inégalités de Bell) qui serait dues à une influence ou à un signal quelconque, classique, de vitesse infra-luminique se propageant entre les deux particules.
Enfin, le schéma expérimental utilisé par toutes ces expériences était très éloigné du schéma « idéal » utilisé par John Bell pour démontrer ses inégalités : on n'était donc pas certain que les inégalités de Bell puissent s'appliquer telles quelles à ces expériences.
Les expériences d'Aspect (1980-1982)
Il manquait alors une expérience décisive vérifiant la réalité de l'état d'intrication quantique, sur la base de la violation des inégalités de Bell. Alain Aspect propose en 1975 une expérience suffisamment rigoureuse pour être irréfutable, qu'il décrit dans son article : Proposed experiment to test the nonseparability of quantum mechanics[5] - [6].
Alain Aspect a spécifié son expérience pour qu'elle puisse être la plus décisive possible, c'est-à-dire :
- Elle doit avoir une excellente source de particules intriquées, afin d'avoir un temps d'expérience court, et une violation la plus nette possible des inégalités de Bell.
- Elle doit mettre en évidence non seulement qu'il existe des corrélations de mesure, mais aussi que ces corrélations sont bien dues à un effet quantique (et par conséquent à une sorte d'influence instantanée), et non à un effet classique qui se propagerait à une vitesse inférieure ou égale à celle de la lumière entre les deux particules.
- Le schéma expérimental doit être le plus proche possible du schéma utilisé par John Bell pour démontrer ses inégalités, afin que l'accord entre les résultats mesurés et prédits soit le plus significatif possible.
Rappel du schéma « idéal » de John Bell
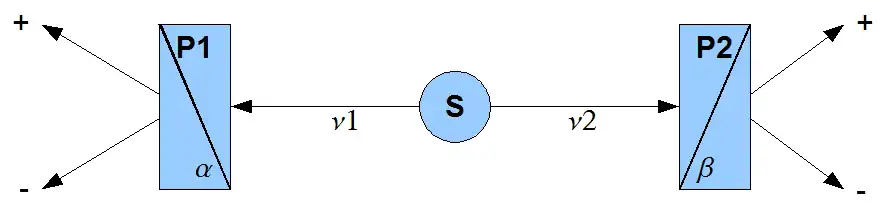
Le schéma ci-dessus représente le schéma de principe à partir duquel John Bell a démontré ses inégalités : une source de photons intriqués S émet simultanément deux photons et dont la polarisation est préparée de telle manière que le vecteur d'état de l'ensemble des deux photons soit :
Cette formule signifie tout simplement que les photons sont en état superposé : tous les deux en polarité verticale, ou tous deux en polarité horizontale, perpendiculaire, avec une probabilité égale.
Ces deux photons sont ensuite mesurés par deux polariseurs P1 et P2, chacun ayant un angle de mesure paramétrable α et β. Le résultat de la mesure de chaque polariseur est (+) ou (–) selon que la polarisation mesurée est respectivement parallèle ou perpendiculaire à l'angle de mesure du polariseur.
Il y a un point important à souligner ici : les polariseurs imaginés dans cette expérience idéale donnent un résultat mesurable dans le cas (+) ET dans le cas (–). Ce n'est pas le cas de tous les polariseurs réels : certains détectent le cas (+) par exemple, et ne détectent rien (le photon ne ressort pas du polariseur) pour le cas (–). Les premières expériences, relatées ci-dessus, utilisaient ce genre de polariseur. Les polariseurs utilisés par Alain Aspect détectent bien les deux cas (+) et (–), se rapprochant ainsi de l'expérience idéale.
Étant donné le dispositif et l'état de polarisation initial donné aux photons, la mécanique quantique permet de prédire les probabilités de mesurer (+,+), (–,–), (+,–) et (–,+) sur les polariseurs (P1,P2), orientés sur les angles ; pour rappel :
On peut démontrer (voir article Inégalités de Bell) que la violation maximale des inégalités est prévue pour °.
Description du dispositif expérimental
Alain Aspect (avec la collaboration des physiciens Philippe Grangier, Gérard Roger et Jean Dalibard[7]) a réalisé un certain nombre d'expériences, de plus en plus complexes, entre 1980 et 1982.
Seule l'expérience la plus complète, réalisée en 1982, et s'approchant le plus des spécifications initiales sera décrite ici.
Source de photons
Les premières expériences réalisées testant les inégalités de Bell, possédaient des sources de photons de faible intensité, nécessitant des temps d'expérience en continu de l'ordre de la semaine. Une des premières améliorations apportée par Alain Aspect est d'utiliser une source de photons de plusieurs ordres de grandeur plus efficace. Cette source permet un taux de détection de 100 photons par seconde, aboutissant à un temps d'expérience maximal de 100 secondes.
La source utilisée est une cascade atomique d'atomes de calcium, excitée à l'aide d'un laser à krypton.
Polariseurs à orientation variable et en position éloignée
Un point très important qui devait être testé par cette expérience est qu'il fallait s'assurer que les corrélations entre les mesures faites par P1 et P2 ne soient pas induites par des effets d'origine « classique », et notamment par des artefacts expérimentaux.
Par exemple, si l'on prépare les polariseurs P1 et P2 avec des angles fixes donnés α et β, on peut toujours imaginer que cet état fixe génère des corrélations parasites via des boucles de courant, de masse, ou autres effets. Car les deux polariseurs font partie d'une même installation et peuvent très bien être influencés l'un l'autre via les divers circuits du dispositif expérimental, et générer des corrélations lors de la mesure.
On peut également imaginer que l'orientation fixe des polariseurs influe, d'une manière ou d'une autre, sur l'état avec lequel le couple de photons est émis. Dans ce cas, les corrélations de mesure pourraient s'expliquer par des variables cachées au niveau des photons, dès l'émission. (Ces observations avaient été faites à Alain Aspect par John Bell lui-même).
Une manière incontestable de mettre hors de cause ce genre d'effets — quels qu'ils soient — est que l'orientation (α,β) des polariseurs soit déterminée au dernier moment (après l'émission des photons, et avant la détection) et qu'ils soient suffisamment éloignés l'un de l'autre pour qu'aucun signal n'aie le temps d'aller de l'un à l'autre.
De cette manière, on ne peut invoquer ni une influence de l'orientation des polariseurs au niveau de l'émission des photons (car lors de l'émission, l'orientation est encore indéterminée), ni une influence d'un polariseur sur l'autre (car les polariseurs sont trop éloignés l'un de l'autre pour pouvoir s'influencer).
En conséquence, dans le dispositif expérimental d'Aspect, les polariseurs P1 et P2 étaient séparés de 6 m de part et d'autre de la source, et de 12 m l'un de l'autre. Cela donnait un temps de 20 ns entre l'émission des photons et la détection : c'est le laps de temps extrêmement court pendant lequel il fallait décider de l'orientation et orienter les polariseurs.
Comme il est physiquement impossible de changer matériellement l'orientation d'un polariseur dans ce laps de temps, deux polariseurs par côté ont été utilisés, pré-orientés différemment. Un « aiguillage » à très haute fréquence de basculement orientait aléatoirement le photon vers l'un ou l'autre de ces polariseurs. L'ensemble de ce dispositif était équivalent à un seul polariseur dont l'angle de polarisation bascule aléatoirement.
Comme il n'était pas possible non plus de provoquer le basculement des aiguillages par l'émission du couple de photons, chaque aiguillage basculait en fait périodiquement avec une période de 10 ns, de manière asynchrone avec l'émission des photons. Mais étant donné la période, on était assuré que l'aiguillage bascule au moins une fois entre l'émission d'un photon et sa détection.
Polariseurs à deux canaux
Une dernière caractéristique importante de l'expérience de 1982 est l'utilisation de polariseurs à deux canaux, permettant d'avoir un résultat mesurable dans le cas (+) comme dans le cas (−). Les polariseurs utilisés jusqu'à l'expérience d'Aspect donnaient une détection dans le cas (+), et on n'obtenait aucune détection dans le cas (−). Ces polariseurs mono-canal avaient deux inconvénients majeurs :
- On ne pouvait facilement discerner le cas (−) d'une erreur d'expérimentation ;
- Ils devaient être soigneusement calibrés.
Les polariseurs à deux canaux utilisés par Aspect dans son expérience évitent ces deux inconvénients et permettent d'utiliser directement les formules de Bell pour calculer les inégalités.
Techniquement, les polariseurs utilisés étaient des cubes polarisants, transmettant une polarité et réfléchissant l'autre, émulant un dispositif de Stern-Gerlach.
Résultats de l'expérience
Les inégalités de Bell permettent d'établir une courbe théorique du nombre de corrélations (+ + ou – –) entre les deux détecteurs par rapport à l'angle relatif des détecteurs . La forme de cette courbe est caractéristique de la violation des inégalités de Bell. L'adéquation des mesures à la forme de la courbe permet donc d'établir, quantitativement et qualitativement, cette violation.
Les expériences d'Aspect ont confirmé sans ambiguïté la violation des inégalités de Bell comme le prévoyait l'interprétation de Copenhague de la mécanique quantique, infirmant par là même la vision réaliste locale d'Einstein de la mécanique quantique et les scénarios à variables cachées locales. Non seulement la violation était confirmée mais de plus, elle était confirmée exactement de la manière prédite par la mécanique quantique, avec un accord statistique jusqu'à 40 écarts types.
Étant donné la qualité technique de l'expérience, le soin apporté pour éviter les artefacts expérimentaux et l'accord statistique quasiment parfait, cette expérience a largement convaincu la communauté scientifique de la réalité de la violation des inégalités de Bell par la physique quantique et par conséquent, de la réalité de la non-localité quantique.
Limites de l'expérience
Après ces résultats, certains physiciens ont légitimement continué à rechercher les failles de l'expérience d'Aspect et comment elle pourrait être améliorée pour ne prêter le flanc à aucune critique.
Il s'avère que des objections théoriques peuvent être opposées à ce dispositif :
- l'aspect quasi périodique des oscillations de l'aiguillage est gênant car cela peut induire des corrélations par une quasi-synchronisation résultante des deux aiguillages ;
- les corrélations (+,+), (–,–) etc. étaient comptées en temps réel, au moment de la détection. Cela implique que les deux canaux (+) et (–) de chaque polariseur étaient reliés entre eux, par des circuits physiques. Là encore on peut imaginer que cela induise des corrélations.
Une expérience « idéale », évacuant toute possibilité imaginable de corrélations induites, devrait donc :
- avoir un aiguillage purement aléatoire et non quasi périodique ;
- enregistrer les résultats (+) ou (–) de chaque côté du dispositif, sans lien physique entre les deux côtés. Les corrélations seraient calculées après l'expérience, en comparant les résultats enregistrés des deux côtés.
Les conditions de l'expérience présentaient en outre une faille de détection[1].
Expériences récentes
Les dernières failles mentionnées ci-dessus n'ont pu être réellement comblées qu'à partir de 1998. Entre-temps, l'expérience d'Aspect a été reproduite et la violation des inégalités de Bell a systématiquement été confirmée, avec une certitude statistique allant jusqu'à 100 écarts types.
D'autres expériences ont été menées pour tester les violations des inégalités de Bell avec d'autres observables que la polarisation, afin d'être encore plus proche de l'esprit original du paradoxe EPR, où Einstein imaginait de mesurer sur une paire EPR deux variables conjuguées (comme la position et la quantité de mouvement) : une expérience a été réalisée mettant en jeu les variables conjuguées (temps, énergie), avec là encore confirmation de la mécanique quantique[8].
En 1998, l'expérience de Genève[9] a testé les corrélations entre deux détecteurs distants de 30 kilomètres, en utilisant le réseau suisse de télécommunication par fibre optique. Cette distance laisse beaucoup plus de temps pour commuter les angles des polariseurs et il a donc été possible de mettre en place un aiguillage purement aléatoire. D'autre part, les deux polariseurs éloignés étaient complètement indépendants et les mesures ont été enregistrées de chaque côté, puis comparées après l'expérience, en datant chaque mesure à l'aide d'une horloge atomique. La violation des inégalités de Bell a une nouvelle fois été vérifiée dans ces conditions strictes et presque idéales. Si l'expérience d'Aspect impliquait qu'un hypothétique signal de coordination se déplace deux fois plus vite que c, celle de Genève arrivait à 10 millions de fois c.
À cette date, il ne restait qu'une seule faille imaginable recensée : les détecteurs n'ayant pas une sensibilité parfaite (100 %), il existe toujours des cas où les corrélations ne sont pas détectées, alors qu'elles auraient dû l'être dans l'idéal. Il restait donc l'ultime possibilité que les corrélations non détectées vérifient toujours les inégalités de Bell, faisant en sorte que le total vérifie globalement les inégalités de Bell (après tout, on ne peut pas, en toute rigueur, l'exclure).
En 2000, une expérience a eu lieu à Boulder sur les intrications d'ions piégés, avec une méthode de détection des corrélations très efficace[10]. La fiabilité de détection a été prouvée suffisante pour que l'expérience viole tout de même globalement les inégalités de Bell, même si toutes les corrélations non détectées ne les violaient pas.
En 2001, l'équipe d'Antoine Suarez, comprenant Nicolas Gisin, qui avait participé à l'expérience de Genève, reproduit l'expérience avec cette fois des miroirs ou des détecteurs en mouvement, permettant d'inverser l'ordre des événements d'un référentiel à l'autre, conformément à la relativité restreinte (rappelons que cette inversion n'est justement possible que pour les événements dont l'un n'est pas la cause de l'autre). Les vitesses sont choisies telles que quand chaque photon se réfléchit ou traverse le miroir semi-transparent, dans le référentiel attaché à ce miroir, l'autre photon s'est déjà réfléchi ou a traversé l'autre miroir (configuration « après-après » — en fait pour cette configuration, des ondes acoustiques jouaient le rôle de miroirs semi-transparents). Respectivement, une autre configuration testée permet que chaque photon soit reçu par un détecteur animé d'un mouvement tel que, dans le référentiel de ce détecteur, l'autre photon n'ait pas encore été détecté, qu'il ait traversé ou se soit réfléchi (configuration « avant-avant »). Dans cette expérience également, les inégalités de Bell sont violées[11].
Conclusion
Aujourd'hui, en 2023, la violation des inégalités de Bell par la physique quantique est clairement établie. On utilise d'ailleurs concrètement la violation des inégalités de Bell dans certains protocoles de cryptographie quantique, où la présence d'un espion est détectée par le fait que les inégalités de Bell ne sont plus violées.
On doit donc admettre la non-localité de la physique quantique et la réalité de l'état d'intrication.
La causalité relativiste est-elle remise en question par l'expérience d'Aspect ?
Cette question se pose du fait d'une présentation des faits courante, selon laquelle « un objet quantique présente un état qui dépend instantanément de l'état d'un autre objet avec lequel il a été intriqué ». Cette présentation en terme « d'influence non locale », est souvent utilisée dans les articles de vulgarisation, mais aussi (et volontairement) par certains scientifiques qui se réclament réalistes comme Alain Aspect lui-même, ou Bernard d'Espagnat[12].
Il y a alors au moins trois possibilités :
- La première est que l'on doit se contenter d'appliquer des calculs qui donnent des résultats en accord avec l'expérience, sans se référer à une explication tirée de notre logique, « macroscopique » ou autre. Cette approche, dérivée de l'interprétation de Copenhague, est la plus communément admise parmi les physiciens. Elle est fondée sur le fait qu'aucune explication des phénomènes EPR ne donne lieu à des vérifications ou des prédictions mesurables. En conséquence, la majorité des physiciens considère que les explications de cette expérience tombent en dehors du champ de la science (voir le critère de réfutabilité de Karl Popper). En effet, la majorité des explications manquent de formalisation théorique, et pour celles qui en possèdent, ne proposent pas de vérifications mesurables. Il s'agit donc ici d'une approche empirique, visant à éviter toute dérive en dehors du champ de la science. Les physiciens David Bohm et Basil Hiley, dans leur ouvrage : The Undivided Universe: An Ontological Interpretation of Quantum Theory [« L'Univers indivis : une interprétation ontologique de la théorie quantique. »], estiment qu'il n'existe aucun bien-fondé aux objections au concept de non-localité[13]. Répondant à ceux qui jugent que l'acceptation de la non-localité minerait la possibilité d'isoler et d'observer scientifiquement quelque objet que ce soit, Bohm et Hiley opposent le fait que, dans le monde macroscopique, cette science est possible, puisque les effets de non-localité, montrent-ils, ne sont pas significatifs : l'interprétation permet exactement le même degré de séparabilité des systèmes que ce qui est requis par le « type de travail scientifique qui est effectué dans les faits ». Accorder la théorie de la relativité restreinte avec la non-localité (voir Paradoxe EPR) est une autre question plus complexe, mais Bohm, comme John Stewart Bell[14], soulignera que ce n'est pas une transmission de signaux qui est en jeu dans la notion de non-localité.
Bohm et Hiley, comme Bell, voient dans le rejet de la non localité des facteurs autres que scientifiques :
| John Bell : Présentation au CERN (1990). | Hiley et Bohm : Sur les objections au concept de non-localité. (1993) |
|---|---|
| [L]'idée même d'action à distance est très répugnante pour les physiciens. Si j'avais une heure pour le faire, je vous bombarderais de citations de Newton, d'Einstein, de Bohr et de tous les autres grands hommes, vous disant combien il est impensable que, en faisant quelque chose ici, nous pouvons changer une situation lointaine. Je pense que les pères fondateurs de la mécanique quantique n'avaient pas tellement besoin des arguments d'Einstein sur la nécessité qu'il n'y ait pas d'action à distance, parce qu'ils regardaient ailleurs. L'idée qu'il y ait soit déterminisme, soit action à distance, leur était si répugnante qu'ils détournèrent le regard. Eh bien, c'est la tradition, et nous devons apprendre, dans la vie, parfois, à apprendre de nouvelles traditions. Et il se pourrait bien que nous devions apprendre non pas tant à accepter l'action à distance, mais à accepter l'insuffisance de « pas d'action à distance »[14]. | [Les objections à la non-localité] semblent être plus ou moins de l'ordre d'un préjugé qui s'est développé avec la science moderne. [...] Au début du développement de la science, il y eut un long combat pour se libérer de ce qui pourrait bien avoir été perçu comme des superstitions primitives et des notions magiques, où la non-localité était clairement une notion-clé. Peut-être reste-t-il une peur profondément enracinée que le simple fait de considérer l'idée de non-localité pourrait rouvrir les vannes qui nous protègent de ce qui est perçu comme des pensées irrationnelles tapies sous la surface de la culture moderne. Même si c'était le cas, ce ne serait pas un argument valable contre la non-localité[13]. |
- La deuxième est que l'intrication a « unifié » les deux objets qui ont été soumis à une interaction : ces deux objets restent « un » malgré leur éloignement spatial (« non-localité de Bernard d'Espagnat »). Cet éloignement peut, en fait, même être temporel : il est fondamentalement spatio-temporel. Aucune explication n'est, pour le moment, donnée à ce qui est considéré comme un résultat d'expérience et non pas une explication ou une interprétation de ce résultat. Cette approche qui veut en final expliquer les faits d'expérience est celle des rationalistes.
- La troisième consiste à changer notre conception de la causalité et à accepter le principe d'une causalité rétrograde (un flux causal venant du futur et allant vers le passé), qu'on ne peut toutefois assimiler à la « cause finale », « téléologique », des philosophes classiques. Il n'y a personne pour orienter les événements en fonction d'un objectif : la backward causation est de nature identique à la causalité telle que nous la concevons (« causalité efficiente » des classiques), à ceci près qu'elle s'exerce à contre-courant par rapport à l'écoulement du temps, et qu'elle « s'additionne » éventuellement à la causalité « classique ». Cette interprétation exige d'admettre que l'irréversibilité du temps n'est vraie qu'à l'échelle macroscopique (seconde loi de la thermodynamique), ce que refusent d'admettre de nombreux physiciens tel le physicien et philosophe Étienne Klein qui souligne que la flèche du temps est, selon lui, inscrite dans les symétries de la physique des particules. Cette interprétation a un succès certain auprès de ceux qui développent des interprétations ésotériques de l'expérience, l'employant pour rendre « acceptables » des phénomènes parapsychologiques pour le moins controversés dans la communauté scientifique (notamment la précognition. Olivier Costa de Beauregard s'est illustré dans la défense de telles thèses[15].) Mais cette interprétation est surtout en contradiction flagrante avec les résultats même des expériences telles que celles-ci ont le plus souvent été réalisées : la ligne d'univers qui relie les événements « mesure P1 » et « mesure P2 » de l'espace-temps est une courbe de genre espace. Car, pour infirmer une interprétation alternative possible des corrélations observées au cours de ces expériences, les expérimentateurs se devaient absolument de montrer que la « causalité » relativiste ne pouvait pas expliquer, au moins en partie, ces mêmes résultats, y compris par des scénarios du genre : « photon informant, par quelque processus relativiste que ce soit, le photon de son état quantique après la première mesure... ». Mais il est parfaitement clair que les précautions prises par les auteurs de ces expériences pour éliminer toutes les explications de type « causale » relativiste éliminent en même temps, selon la conception majoritaire, toute explication de type « rétro-causale ». Finalement, pour les tenants de la conception majoritaire, ce type de conception relève de l'interprétation conjecturale et ne se réfère pas vraiment aux expériences ayant réellement été réalisées. Selon eux, il amène à des interprétations à la limite de la science, ressortit même dans certains cas à la pseudo-science, mêlant la physique quantique à un débat qui n'est pas le sien.
Quoi qu'il en soit, aucun physicien ne pense que les résultats des expériences EPR en général, et de l'expérience d'Aspect en particulier, qui sont en parfait accord avec l'interprétation de Copenhague de la mécanique quantique, remettent en cause, de quelque façon que ce soit, le principe de relativité selon lequel nulle forme d'énergie (matière ou force), et par conséquent, nulle information utilisable, ne peut se déplacer à une vitesse supérieure à celle de la lumière, ni, en conséquence, le principe de causalité relativiste qui en dérive. Il est en effet facile de montrer que l'intrication quantique ne peut être utilisée pour transmettre de façon instantanée quelque information que ce soit d'un point de l'espace-temps à un autre. Les résultats de mesure relatifs à la première particule sont de type aléatoire ; les modifications de l'état de l'autre particule induites par ces mesures, pour instantanées qu'elles soient selon l'interprétation de Copenhague de la mécanique quantique et les résultats de l'expérience d'Aspect, conduisent à des résultats de mesure relatifs à la seconde particule qui sont, en apparence, tout aussi aléatoires : aucune information utilisable ne peut être séparément tirée de ces mesures sur le moment, et les corrélations resteront indétectables tant que les résultats de ces deux séries de mesures ne seront pas comparés. C'est donc la nécessité incontournable, parfaitement mise en évidence par ce type d'expériences, de disposer d'un signal « classique » au sens de la relativité pour transmettre l'information nécessaire à la détection de ces corrélations, signal sans lequel on ne peut rien transmettre et qui détermine la célérité de la transmission d'information, qui vient réaffirmer le principe fondamental de la relativité. Par suite, le principe de causalité relativiste est, lui aussi, parfaitement compatible avec les résultats des expériences EPR.
Notes et références
- Bailly 2015.
- (en) Erwin Schrödinger, « Probability relations between separated systems », Proc. Camb. Phil. Soc., vol. 31, , p. 555-563
- Par exemple si un homme marié se trouvant à plusieurs années-lumière meurt, alors sa femme se retrouve ipso facto veuve aussi, indépendamment du fait que la constatation en demandera plusieurs années
- (en) Clauser, Horne, Shimony, « Proposed experiment to test local hidden-variable theories », Phys. Rev. Lett., vol. 23,
- Nikseresht 2005, p. 235.
- (en) Alain Aspect, « Proposed experiment to test the nonseparability of quantum mechanics », Physical Review D, vol. 14, no 8, (DOI 10.1103/PhysRevD.14.1944)
- « Alain Aspect, prix Nobel de physique 2022 », sur CNRS Le journal (consulté le )
- (en) Brendel, Mohler, Martienssen, « Experimental test of Bell's inequality for Energy and Time », Europhys. Lett., vol. 20, , p. 575
- (en) Weihs, Jennewein, Simon, Weinfurter, Anton Zeilinger, « Violation of Bell's inequality under strict Einstein locality condition », Phys. Rev. Lett., vol. 81, , p. 5039 (résumé)
- (en) Rowe,Keilpinsky,Meyer,Sackett,Itano,Wineland, « Experimental violation of a Bell's inequality with efficient detection », Nature, vol. 409, , p. 791 (résumé)
- (en) Antoine Suarez, Is there a real time ordering behind the nonlocal correlations?, 2001.
- Voir par exemple Corrélations, Causalité, Réalité
- (en) Hiley, B. J.; Bohm, David (trad. de l'allemand), The Undivided Universe : An Ontological Interpretation of Quantum Theory, New York, Routledge, , 397 p. (ISBN 978-0-415-06588-7, LCCN 91021387) p. 157-158.
- John Bell Inequality Video. 22 janvier 1990.
- D'Einstein à la télépathie
Bibliographie
- Sean Bailly, « L’intrication quantique confirmée par une expérience de Bell sans faille », sur Pour la science, (consulté le ).
- Iraj Nikseresht, La physique quantique : origines, interprétations et critiques, Paris, Ellipses, , 270 p. (ISBN 2-7298-2366-2)
- Bernard d'Espagnat, Traité de physique et de philosophie, Fayard (ISBN 2-213-61190-4) Voir le chapitre 3. Non-séparabilité et théorème de Bell
- Bernard d'Espagnat, A la recherche du réel, Bordas (ISBN 2-266-04529-6)
- Bernard d'Espagnat, Étienne Klein, Regards sur la matière (ISBN 2-213-03039-1) Voir le chapitre VIII. La non-séparabilité des couples qui se corrèlent
Voir aussi
Articles connexes
Liens externes
- Vidéo conférence sur l'optique quantique (17 min), par Alain Aspect, Directeur de recherche à l'Institut d'Optique à Orsay.
- Les intrigantes intrications du monde quantique, La conversation scientifique sur France Culture, 29 février 2020
- Intrication quantique : un étrange Aspect de la matière, La méthode scientifique sur France Culture, 14 mai 2019
- Les inégalités de Bell et les expériences d’Alain Aspect – Science étonnante










