Simultanéité
En physique, la simultanéité de deux événements est le fait qu'ils se produisent au même moment.
Dans la physique d'Isaac Newton, le temps est absolu et les informations peuvent se transmettre à vitesse infinie : la force gravitationnelle, par exemple, est supposée se propager instantanément. Et la notion de simultanéité rejoint l'évidence de l'expérience quotidienne : si deux événements se sont produits à la même heure pour un observateur, il en est de même pour tout autre observateur.

Dans l'univers de la relativité restreinte proposée en 1905 par Albert Einstein, l'existence d'une vitesse limite (la vitesse de la lumière) et identique dans tous les référentiels galiléens unifie l'espace et le temps en une entité unique, appelée espace-temps, et leur fait perdre leur caractère absolu. La simultanéité entre deux événements perd son aspect d'évidence et devient aussi relative à l'observateur et son référentiel : deux événements se produisant au même moment pour un observateur donné pourront se produire à des instants différents pour un autre observateur.
Perception immédiate de la simultanéité
Un « événement » est un fait se produisant à un endroit donné et à un instant donné.
De façon immédiate deux événements sont considérés comme simultanés s'ils sont perçus au même instant. Mais une analyse correcte demande que l'on fasse la distinction entre l'émission d'un signal et sa réception par un observateur. Il s'agit en fait de deux événements et non d'un seul.
En physique newtonienne
Certaines interactions (par exemple : la gravitation) sont supposées se transmettre instantanément, autrement dit à vitesse infinie. Ainsi, dès qu'un événement a lieu, l'ensemble de l'univers est susceptible d'en être immédiatement influencé[1]. Donc, si une personne observe deux événements comme étant simultanés, toute personne les observera aussi comme simultanés. Il en est de même dans le cas de deux événements observés comme non-simultanés.
En théorie de la relativité
En relativité restreinte, toute interaction (et toute information) est transmise au maximum à la vitesse de la lumière qui est la même dans tous les référentiels inertiels, ou encore indépendante de la vitesse de sa source[2]. Voici une situation inspirée d'un exemple donné par Einstein[3], relatif à un train :
Supposons qu'au moment précis où le milieu O' d'un train passe devant le point O situé sur la voie, les deux observateurs situés en O' (dans le train) et O (sur le quai) voient deux signaux lumineux qui ont été émis depuis O (et O') vers les deux extrémités du train. Les arrivées de ces signaux aux extrémités du train seront-elles simultanées pour les deux observateurs en O' (dans le train) et O (sur le quai) ?
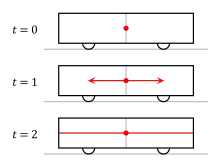
Pour l'observateur dans le train, la lumière est émise depuis un point de l'espace situé au milieu du train, et la vitesse de la lumière étant la même dans toutes les directions de son référentiel (inertiel), les deux signaux arriveront simultanément aux deux extrémités et seront renvoyés simultanément vers lui, au milieu du train.

Pour l'observateur sur le quai, qui voit passer le train, la lumière a été émise depuis un point de l'espace et se diffuse à partir de ce point à la vitesse de la lumière, dans toutes les directions. Cet observateur, comprenant que l'arrière du train va à la rencontre de la lumière cependant que l'avant s'en éloigne, n'est pas surpris que l'arrière du train lui renvoie la lumière avant l'avant du train. Pour cet observateur, les deux signaux n'arrivent pas simultanément aux extrémités du train. C'est ici que l'invariance de la vitesse de la lumière dans tout référentiel diverge de celle d'un objet non relativiste, pour lequel le même observateur à quai perçoit une arrivée simultanée aux deux extrémités du train.
Conclusion : la simultanéité des deux événements, que constituent les arrivées des signaux lumineux aux extrémités du train, est relative à chaque observateur.
Simultanéité et relativité restreinte
Synchronisation des horloges
En relativité restreinte un événement est un fait se produisant à tel endroit, à tel instant. Un événement est identifiable par lui-même (par exemple le départ de la mission Apollo 12), par sa description ou par un nom, et acquiert de ce fait une sorte de caractère universel.
Cependant, la description de l’événement ne prend un sens opérationnel qu'à travers la détermination de sa position spatiale et temporelle dans un repère que la mécanique classique ou la relativité restreinte prend comme galiléen. L'événement est alors décrit en pratique dans ce référentiel par quatre composantes (x,y,z,t) : trois d'espace et une de temps.
La détermination des coordonnées cartésiennes spatiales (x,y,z) se fait par mesure des distances entre un point origine et le point où se produit l'événement. Comme elle est identique dans tous les référentiels galiléens, la vitesse de la lumière peut être utilisée dans ce but[note 1] : on mesure le temps pour faire un aller-retour entre le point choisi et l'origine et on en déduit la distance qui les sépare. En pratique, il suffira d'effectuer cet étalonnage une fois pour toutes et d'attacher à chaque point du référentiel (« à chaque observateur ») l'indication de ses propres coordonnées.
Pour déterminer la coordonnée temporelle t d'un événement dans un repère donné, on place une horloge auprès de chaque observateur de ce repère. La synchronisation des horloges repose sur l'invariance de la vitesse de la lumière, sur la mesure des distances entre les horloges et sur l'isotropie de l'espace-temps. Elle est assurée de la façon suivante. Un administrateur central, gardien du temps, émet un top horaire de référence, disons à midi. Alors lorsqu'un observateur situé à la distance r de l'administrateur central reçoit ce top, il tient compte du temps r /c mis par le signal pour lui parvenir et met son horloge à l'heure (midi + r /c).
À l'issue de cette synchronisation on peut dire que toutes les horloges du référentiel indiquent la même heure. Cette façon de parler n'est peut-être pas tout à fait correcte, puisque personne ne peut voir simultanément toutes les horloges du référentiel considéré, mais elle résume bien le fait que, comme peut le constater n'importe quel observateur recevant les signaux horaires de n'importe quel autre observateur du même repère, une horloge recevra toujours avec le même retard (r / c) le signal en provenance d'une autre horloge située à la distance r et que toutes les horloges battent au même rythme,.
Au bout du compte, un référentiel galiléen est un ensemble d'horloges synchronisées fixes les unes par rapport aux autres et situées en des points portant l'indication de leur position spatiale dans le groupe.
La synchronisation décrite est réservée à un référentiel donné. Le processus indiqué ne permet pas de relier les marches des horloges (même de construction identique) d'un référentiel à l'autre.
Notion de simultanéité en relativité
Deux événements et décrits par leurs coordonnées spatio-temporelles respectives et dans un même référentiel galiléen dont les horloges ont été synchronisées sont dits simultanés si les instants et sont les mêmes. On dit qu'ils sont simultanés, mais en définitive leur simultanéité ne peut être vérifiée par un observateur qu'après coup, quand les informations des horloges lui sont parvenues : l'observateur peut alors dire que les événements étaient simultanés.
Si de plus les positions de ces événements diffèrent par la valeur d'au moins une de leurs coordonnées spatiales, ils ne peuvent pas être liés par une relation de cause à effet par suite de l'existence d'une vitesse limite pour toutes les interactions. Ils sont dits ailleurs l'un de l'autre.
Coïncidence
Deux événements sont dits coïncidants si leurs coordonnées spatio-temporelles exprimées dans le même référentiel sont identiques. Deux événements coïncidants dans un référentiel sont aussi coïncidants dans tout autre référentiel.
On peut ainsi dire qu'un choc entre deux particules examiné dans un référentiel donné est aussi un choc dans tout autre référentiel galiléen. C'est aussi ce qui permet de préciser les quatre coordonnées d'espace-temps d'un événement dans un référentiel : il y a coïncidence entre l'événement et la borne-horloge dont on lira les indications.
Relativité de la simultanéité
Voici une explication donnée par Einstein[3] :
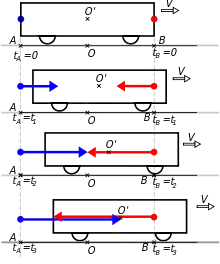
Supposons que dans un référentiel deux éclairs soient déclenchés simultanément, l'un au point A et l'autre au point B. Puisque leurs déclenchements sont simultanés dans ce référentiel, les lumières émises par chacun arriveront simultanément au point O milieu de [AB], ce que l'on voit dans le 3e dessin.
Supposons qu'un observateur O' soit en mouvement vers B à la vitesse constante V et qu'à l'instant du déclenchement (instant observé dans le référentiel de la simultanéité) cet observateur est au point O. Le problème est de savoir si pour cet observateur O' les deux déclenchements sont aussi simultanés.
S'ils le sont aussi dans le référentiel où cet observateur O' est immobile : comme au déclenchement l'observateur est au milieu de [AB] et que dans son référentiel la vitesse de la lumière ne dépend pas de celle de la source, il recevra simultanément les deux rayons lumineux.
S'il ne les reçoit pas simultanément, c'est que leurs émissions ne sont pas simultanées dans son référentiel.
On ne peut pas dessiner ce qui se passe dans le référentiel de O' car on ne sait pas si initialement les deux déclenchements y sont simultanés ou non. Par contre on peut dessiner ce que voit l'observateur en O placé dans le référentiel où l'on est sûr que les déclenchements sont simultanés. Dans les dessins ci-contre, on comprend que cet observateur voit le rayon lumineux rouge atteindre O' avant le rayon lumineux bleu : dans le référentiel de O, il n'y a pas coïncidence entre les rencontres de O' et les rayons rouge et bleu. Donc il n'y a pas coïncidence dans le référentiel de O' non plus !
Conclusion : comme O' ne reçoit pas simultanément les rayons rouge et bleu, leurs émissions ne sont pas simultanées dans son référentiel, alors qu'elles le sont dans celui de O.
Simultanéité et diagramme d'espace-temps
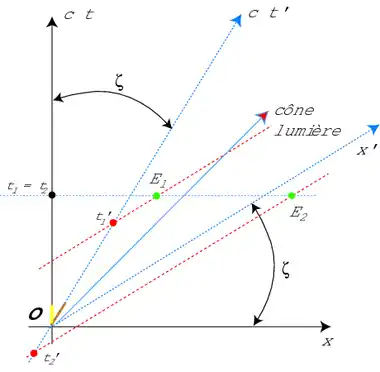
Deux événements, simultanés dans le repère (Ox,ct), ne le sont plus dans le référentiel (O'x',ct') se déplaçant avec une vitesse , selon Ox. Les unités de temps des repères Terre et fusée sont respectivement en jaune et marron.
Le diagramme de Minkowski ci-contre éclaire la relativité de la simultanéité en relativité restreinte. Les repères galiléens (Ox,ct) et (O'x',ct') sont reliés par une transformation spéciale de Lorentz, le second repère se déplaçant à la vitesse .
Géométriquement, choisissant (Ox,ct) comme repère de référence, (O'x',ct') se présente de telle sorte que les axes O'x' et O'ct' sont symétriques par rapport au cône de lumière, chacun s'étant rapproché de l'angle par rapport aux directions correspondantes Ox et Oct donné par :
Les deux événements et sont simultanés dans le repère (Ox,ct). Les axes de temps égaux dans chacun des repères sont les lignes parallèles aux axes Ox et O'x', respectivement. Manifestement dans le cas du schéma, l'événement a lieu avant , vus du repère (O'x',ct').
Un tracé géométrique adéquat des unités permet de vérifier graphiquement l'écart temporel, donné par les transformations de Lorentz :
Cet exemple prend un relief particulièrement saisissant si un des deux événements ci-dessus, , consiste en une mesure de la polarisation d'un photon appartenant à une paire corrélée d'une expérience menée pour mettre en évidence le paradoxe d'Einstein, Podolski et Rosen.
Dans le référentiel (Ox,ct), si on considère que l'opération de mesure effectuée au point sur le photon 1 modifie instantanément la caractéristique correspondante du photon 2 en , alors, dans le référentiel (O'x',ct'), pour que cette interprétation reste valable, il faut admettre que l'influence venue du photon 1 a rebroussé le temps vers le photon 2 (car dans ce référentiel, est plus tardif que ). Et réciproquement, si on considère que c'est la mesure sur le photon 2 qui influence le photon 1, un autre changement de référentiel inverserait la situation entre les deux événements et amènerait la remarque symétrique entre et .
Cette description dans différents référentiels galiléens, contradictoire avec la causalité, suggère que l'intrication quantique est un phénomène acausal par rapport à l'acte de mesure (et ne peut être, à ce titre, utilisée pour propager de l'information), et est non locale, aussi bien spatialement que temporellement. Elle souligne, de manière générale, la difficile cohabitation des principes de la physique quantique et de ceux de la physique relativiste, au moins tels qu'ils sont compris habituellement.
Notes et références
Notes
- On peut encore plus simplement mesurer directement les distances en secondes, ou d'ailleurs les temps en mètres.
Références
- §1 Vitesse de propagation des interactions, dans Lev Landau et Evgueni Lifchits, Physique théorique, t. 2 : Théorie des champs [détail des éditions].
- James H. Smith (trad. de l'anglais), Introduction à la relativité, Paris, InterEditions, , 2e éd., 317 p. (ISBN 2-7296-0088-4). Édition avec exercices corrigésL'ouvrage a été réédité : James H. Smith, Introduction à la relativité, Masson, , 3e éd. (ISBN 2-225-82985-3).
- Albert Einstein (trad. de l'allemand), La Théorie de la relativité restreinte et générale, Paris, Dunod, , 177 p. (ISBN 2-10-048716-7) La version anglaise est publiée par le projet Gutenberg..
Voir aussi
Bibliographie
- V. Ougarov, Théorie de la relativité restreinte, deuxième édition, Éditions Mir, Moscou, traduction française Éditions Mir, 1979.
- Ch. Grossetête, Relativité restreinte et structure atomique de la matière, Ellipses, 1985. (ISBN 2-7298-8554-4)











