Dynamique et gestion des pêcheries

La pêche (halieutique) a influencé le développement de la société, principalement autour des zones côtières et est à l’origine de coutumes ancestrales. Cette activité est aujourd’hui concernée par des enjeux socio-économiques, politiques et écologiques. En termes d’économie, les pêcheries fournissent de nombreux emplois, puisqu'elles contribuent au commerce local et international, mais également au tourisme de certains pays. D’après le dernier rapport de la Food and Agriculture Organization of the United Nations (FAO), l’Asie regroupe 84 % des industriels de la pêche (rapport 2014). D’autre part, avec l’expansion démographique de la population humaine, la demande a fortement augmenté. En plus de 50 ans, le produit des pêches a triplé (de 33,9 millions de tonnes en 1960 à 91,3 millions de tonnes en 2012) et la consommation de poissons par habitant a doublé, passant alors de 10 kg en 1960 à 19 kg en 2012. Au-delà de l’utilisation alimentaire, il existe de nombreux sous-produits de la pêche pouvant être revalorisés en biogaz, maquillage, engrais, gélatine, etc. ; ce qui augmente le rendement économique des industries de pêche.

D’un point de vue social, de nombreux facteurs accentuent la difficulté de gérer ce secteur d’activité, comme les traditions, les savoir-faire des pêcheurs, la gastronomie et le patrimoine propre à chaque région. De plus, certaines questions posent des problèmes en termes d’éthique et les politiques appliquées varient d’un pays à l’autre, voire d'une région à l'autre, en adéquation avec la biodiversité du site. Ces enjeux montrent bien l’importance des pêcheries dans le développement des populations humaines. Toutefois, le premier paramètre affeté par les activités de pêche est l’environnement et une exploitation démesurée du milieu risque de faire baisser la rentabilité du secteur. En 2011, 29 % des stocks de poissons marins issus de pêches commerciales étaient surpêchés (rapport FAO, 2014).

Les pêches ont des effets directs sur les populations naturelles en réduisant l’abondance des espèces ciblées, en perturbant leurs cycles de vie et en augmentant la mortalité des espèces non visées qui sont pêchées accidentellement. Les effets indirects ont des conséquences à plus grande échelle, sur l’habitat des espèces et l’équilibre de l’écosystème. À la suite de la prise de conscience des impacts écologiques des pêcheries sur les écosystèmes marins, la gestion intègre des objectifs de maintien de la biodiversité, pour un respect de l’environnement et une activité durable[1] - [2].

La pêcherie est une activité exploitant les populations naturelles, et chaque pêcherie exploite une ressource halieutique spécifique. Une réglementation est donc nécessaire et doit être appliquée en tenant compte de plusieurs facteurs, notamment en termes de conservation. Des lois permettent de réguler les quotas de pêche selon différents critères tels que la dynamique de la population visée, le cycle de vie des espèces, mais elles visent aussi le comportement des pêcheurs (engins de pêche adaptés, limite de la zone d'exploitation, respect du milieu). Les réglementations et limites imposées sont spécifiques de chaque pays en fonction de leurs besoins, ou de leurs habitudes alimentaires (cas du Japon). Au vu de l'ampleur de cette activité, des traités internationaux ont été signés entre plusieurs états dans le but de s'engager mutuellement dans l'exploitation d'une ressource de pêche. D'autres formes de réglementations existent à différents niveaux comme les normes industrielles, mais toutes ces lois sont mises en place dans l'optique d'assurer la pérennité des pêcheries[3].

La dynamique des pêcheries étant complexe et variable, il faut des systèmes permettant de prévoir leur évolution dans le temps. La gestion doit être spécifique et conçue en adéquation avec les réglementations et les objectifs de chaque pêcherie. Plusieurs étapes sont nécessaires afin d'avoir une bonne vision de l'ensemble des données et des informations qui sont à prendre en compte. L'aménagement d'une pêcherie nécessite une étude minutieuse.

Plusieurs paramètres doivent être inclus lors de sa conception et les gestionnaires doivent avoir une bonne connaissance de leur pêcherie afin d'assurer la mise en place d'une gestion efficace. Les études scientifiques menées sur les dynamiques des populations exploitées et des pêcheries constituent un support indispensable pour établir de bonnes stratégies de gestion. Elles fournissent des données essentielles qui peuvent être de types biologiques (quantité de poissons, effort de pêche, composition par espèces, zones exploitées), et écologiques (captures d'espèces pêchées accidentellement comme certaines espèces indicatrices, impacts des engins de pêche sur la faune et la flore aquatique, modification des habitats naturels, zones protégées à prendre en compte pour la conservation des espèces). Les scientifiques s'appuient sur ces données, tout en considérant les aspects économiques et sociaux, pour élaborer des modèles de gestion des pêcheries, selon différents paramètres en jeu. La modélisation permet aux gestionnaires de visualiser l'évolution d'une stratégie sur le long terme. Les modèles mathématiques sont ainsi étudiés pour garantir un maximum de bénéfices pour les pêcheurs, tout en préservant les populations naturelles exploitées.

Il existe de très nombreux modèles mathématiques élaborés selon différents paramètres, et permettent de faire des projections sur l’évolution de la pêcherie et des stocks de populations naturelles. La dynamique de ces populations dépend fortement de facteurs biologiques, comme le taux d'accroissement de la population qui comprend la natalité et la mortalité, ainsi que les mouvements d'individus (immigration et émigration). L'activité humaine constitue également un facteur important qui influence la dynamique des populations. Les contraintes majeures à prendre en compte dans la gestion d'une pêcherie sont donc de types économiques, comme la demande du marché qui évolue avec le prix de vente; ou encore comportementales et conservationnistes. Les variables à intégrer dans les modèles de gestion sont le taux de croissance de la population, l'effort qui correspond au nombre et à la durée de l'exploitation, les coûts liés à l'effort, la capture dans la ressource (capturabilité), ainsi que les prix de vente des captures.

Les modèles peuvent alors être catégorisés en deux parties, ceux purement biologiques qui ne prennent pas en compte les intérêts économiques, et ceux bioéconomiques qui intègrent le rendement et les bénéfices des pêcheurs. 

D'après le modèle de dynamique de population de Malthus, la densité de population d’un stock suit l'équation suivante :

${\displaystyle N_{(}(t+1))=N_{t}+dN/dt}$

(1)

Pour une exploitation durable des ressources, il faut seulement prélever le surplus du stock. Ainsi la population initiale ne sera pas affectée par l'activité et restera à l'équilibre. Sur l'équation (1) cela revient à dire :

${\displaystyle dN/dt=0}$ (2) soit ${\displaystyle N_{(}(t+1))=N_{t}}$

(3) En utilisant le modèle de Verhulst :

${\displaystyle {\frac {dN}{dt}}=rN(1-{\frac {N}{K}})-F}$

(4)

D'après (2) et (4) il y a une exploitation durable si et seulement si : 

${\displaystyle rN(1-N/K)=F}$

(5)

L'équilibre est atteint lorsque le recrutement R, est égal à la mortalité par exploitation F. L’exploitation du stock peut être soumise à différentes gestions permettant de contrôler le taux de mortalité. Un quota de capture peut être fixé, indépendant de la densité de population, mais il est également possible de faire varier le taux de mortalité en fonction des paramètres (biologiques ou économiques)  du système. 

Courbe de dynamique du stock à TAC.

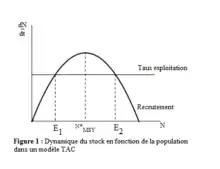
Dans ce modèle, le nombre total de captures autorisées est fixe, la mortalité par exploitation sera constante :

${\displaystyle F=constante}$ et ${\displaystyle R=rN(1-N/K)}$

(6)

Il existe deux équilibres où ${\displaystyle dN/dt=0}$

L'équilibre E₂  est stable tandis que E₁ est instable. Cela signifie que l'application d'un TAC (Total autorisé de capture) sur une population à forte densité laisse un stock constant et stable, alors que pour une faible densité de population, le stock risque de s’effondrer et de disparaître. 

Plus le TAC va être faible et plus les deux équilibres seront éloignés : à forte densité de population, l’équilibre reste stable. Cet idéal pose un problème d'un point de vue purement économique. En effet, un faible TAC pour les pêcheurs, limite leur nombre de captures et limite également leurs revenus. Ils ont alors tendance à pêcher plus afin d'arriver à un Rendement d’Exploitation Durable Maximale (Maximum Sustainable Yield, MSY). Dans ce cas les 2 équilibres se retrouvent confondus en un équilibre instable. Le modèle montre ici une limite puisqu’il ne permet pas d’exploiter au maximum les ressources[4].

Après l’instauration des TAC, les gestionnaires ont affiné le modèle en créant le Quota Indiduel Transferable ou Individual Transferable Quota (ITQ). Dans ce type de gestion le gouvernement attribue à chaque acteur de la pêcherie un quota de pêche et chaque quota est entièrement divisible. Les quotas étant transférables, un titulaire peut revendre la totalité ou des fractions du quota qui lui est alloué à d'autres acteurs de la pêcherie. Le problème que pose cette méthode est d'aboutir à un risque de monopolisation de la pêcherie par les plus gros acteurs[5].

Courbe de la dynamique du stock à effort constant

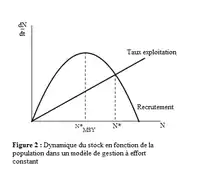
Un autre modèle propose d’appliquer un effort constant sur le stock et de contrôler le nombre de captures en fonction de la densité de population.

D'où :  

${\displaystyle F=qEN}$ (7)

En utilisant cette méthode, il y a seulement un équilibre stable et ce, même si le MSY est atteint.

Le MSY est au maximum de la fonction de recrutement :

${\displaystyle {\frac {\partial rN(1-{\frac {N}{K}})}{\partial N}}=0}$ soit ${\displaystyle r-{\frac {2rN}{K}}=0}$
${\displaystyle {\frac {2N}{K}}=1}$
${\displaystyle N={\frac {K}{2}}}$ (8)

En remplaçant (8) dans (6) et dans (7), cela donne :

${\displaystyle MSY=qE{\frac {K}{2}}}$
${\displaystyle MSY=r{\frac {K}{2}}(1-{\frac {K}{2K}})={\frac {rK}{4}}}$ (9)

Pour tendre vers un point d’équilibre N*, il faut que le taux de croissance r soit supérieur au produit de la capturabilité et de l’effort de pêche : qEN* > 0 si et seulement si qE < r

Il est possible de calculer la densité de population à l'équilibre, N*, en fonction de l'effort, E :

${\displaystyle {\frac {dN}{dt}}=0}$ soit ${\displaystyle rN^{*}(1-{\frac {N^{*}}{K}})=qEN^{*}}$

${\displaystyle 1-{\frac {N*}{K}}={\frac {qE}{r}}}$

${\displaystyle N^{*}=K-{\frac {qK}{r}}E}$ (10)

Ce qui donne une droite d'ordonnée à l'origine K et de pente ${\displaystyle {\frac {-qK}{r}}}$

On peut également calculer le rendement à l'équilibre en remplaçant (10) dans (7) :

${\displaystyle F(N^{*})=qEN^{*}=qEK(1-{\frac {qE}{r}})}$

Les paramètres K et r peuvent être estimés d'après (9) si q est connu : ${\displaystyle r=2qE_{MSY}}$

Grâce à ce type de gestion, les ressources peuvent être exploitées au maximum et cela permet d’estimer les paramètres du stock. Cependant, ce modèle suppose que K et r sont constants et que l'équilibre du système est atteint instantanément, alors qu’en réalité, la stochasticité agit sur les paramètres du système. De plus, il est difficile de faire respecter un effort constant, car la densité de population agit sur l'effort via le prix. La raréfaction d’une espèce augmente son prix de vente et tend à augmenter l’effort. Il est possible de complexifier ce modèle, en prenant en compte le fait qu'il existe une corrélation positive entre la densité du stock et le taux de croissance des individus qui le composent, appelée effet Allee ou densité dépendance positive du système.

(6) devient :

Avec ${\displaystyle {\frac {N}{A}}-1}$ : coefficient d’accélération

${\displaystyle R=rN(1-{\frac {N}{K}})({\frac {N}{A}}-1)}$ (11)

Et (4) devient :

${\displaystyle {\frac {dN}{dt}}=rN(1-{\frac {N}{K}})({\frac {N}{A}}-1)-qEN}$ (12)

Il existe alors deux points d'équilibres : E1 instable et E2 stable. L'ajout de la densité dépendance positive déstabilise le système précédent, il faut garder le stock loin du point E1 et donc limiter l’effort pour conserver l’équilibre. S'il y a effet Allee, le stock ne peut plus être exploité au MSY, car l'équilibre est semi stable et la population risquerait de s’effondrer à cause des facteurs stochastiques[6] - [7].

Les modèles bioéconomiques permettent d'évaluer la rentabilité de l'activité, en incluant les paramètres économiques. L'aspect commercial des pêches peut être évalué avec ou sans gestion. La différence entre les bénéfices va résider entre la mise en commun ou non des ressources (assimilable à la théorie des jeux).

Courbe du bénéfice en fonction de l'effort.

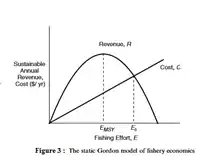
Dans ce cas, aucune régulation de l'activité n'est considérée, les prédictions portent alors sur les bénéfices de la pêche selon l'effort et non plus sur la densité de population du stock. Le bénéfice B de la pêcherie dépend du prix de vente, du nombre d’individus capturés, du coût de l’effort de pêche et de l'effort.

D’où :  

${\displaystyle B(E)=pY-cE}$ (13)

      Or :

Y=F et ${\displaystyle N^{*}=K(1-{\frac {qE}{r}})}$

alors : 

${\displaystyle B^{*}(E)=pqEK(1-{\frac {qE}{r}})-cE}$ et ${\displaystyle E^{*}=r/q(1-{\frac {c}{pqK}})}$

Graphiquement, lorsque l'effort correspondant au MSY est dépassé, il y a une diminution des bénéfices. De plus, l'équilibre du système est alors atteint lorsque les revenus sont nuls. Une pêcherie non gérée (en libre accès), n'est pas économiquement rentable, puisque l'effort de pêche dépassera l'effort au MSY et le système tendra vers un équilibre sans bénéfices.

Le modèle sans gestion a montré qu'il était impossible de faire des bénéfices individuels, sans réduire l'effort collectif  de la pêcherie. Cela  révèle  un conflit entre intérêt personnel et intérêt du groupe, qui aboutit à un échec économique. Il faut donc réduire l’effort tout en maximisant les gains. Ainsi, le point MEY (Maximum Economic Yield)  est défini comme l'effort pour un rendement économique maximum. Ce point correspond au maximum de la courbe des bénéfices, pour le déterminer, il suffit de trouver le point de la courbe pour lequel la pente est nulle :

${\displaystyle {\frac {\partial B(E)}{\partial E}}=0}$ soit : ${\displaystyle pqK-{\frac {2pq^{2}K}{r}}E_{MEY}=0}$

${\displaystyle E_{MEY}=r/2q(1-c/pqK)}$

Et d'après (14) :

${\displaystyle E_{MEY}=1/2E^{*}}$

Étant donné que l'effort pour optimiser le bénéfice (E_MEY) est inférieur à l'effort du point d'équilibre(E*), le but est de baisser l’effort pour que le point d’équilibre  tende vers E_MEY.

Différentes stratégies de gestion ont donc été élaborées. La première consiste à réguler l'effort par la mise en place de périodes de fermeture des zones de pêche. Cette méthode a des limites : lors des périodes de fermeture les bénéfices vont diminuer, alors qu’en périodes d'ouverture l'effort de pêche va fortement augmenter (via une optimisation des engins et des techniques de pêche par exemple). Cela induit un coût d’exploitation plus important et un déclin de la population. Une autre stratégie consiste à créer au sein des pêcheries, des Aires Marines Protégées (AMP) permettant de diminuer de manière efficace et durable l'effort de pêche appliqué[8].

Une des stratégies permettant une gestion durable est la mise en place d'aires marines protégées. Les AMP sont intéressants d'un point de vue écologique puisqu'elles contribuent à la conservation des ressources naturelles et à la protection de certaines espèces menacées. Ces zones réglementées sont interdites aux activités de pêche. Leurs intérêts sont multiples, mais en ce qui concerne la gestion des pêcheries, l'intérêt majeur est la restauration des milieux naturels, trop longtemps soumis aux exploitations par l'Homme. Ceci permet aux populations de poissons surpêchées de se reproduire et d'arriver à reconstituer une biomasse importante. En ce sens, les AMP présentent un avantage indirect pour les pêcheurs qui vont pouvoir capturer les poissons en surplus, issus des zones protégées.

Des scientifiques ont tenté d'évaluer l'efficacité des AMP sur la reconstitution des stocks de poissons en déclin, notamment sur l'exemple des populations de cabillaud de la mer Baltique orientale. Des études se basent sur un modèle spatio-temporel appelé ISIS-Fish pour tester les performances des zones protégées déjà mises en place, selon différentes conditions de forçages environnementaux. Le recrutement des populations de cabillaud dépend de la teneur en oxygène dans l'eau, qui est influencée par les courants océaniques et atmosphériques. Les observations ont donc été réalisées sur le long terme, prenant en compte des caractéristiques environnementales favorables et défavorables. Les résultats montrent qu'en conditions favorables (dans un environnement stable), l'effort de pêche sera durable même sans aucune fermeture de zones. Or dans des conditions défavorables, aucun scénario spécifique de clôture n'est efficace. Une évaluation des différents moyens de gestion de fermetures a également été effectuée, sans prendre en compte cette fois les variations de l'environnement. Les résultats montrent que la diminution de l'effort et de la mortalité due aux saisons de fermeture de pêche, est bénéfique pour la reconstitution des stocks de poissons[9].

L'aquaculture permet de restaurer certaines espèces de poissons soumises aux pressions de pêche. Il s'agit d'une pratique qui s'est largement développée au cours de cette dernière décennie, en fonction de la demande du marché. Aujourd'hui, plus de 200 espèces de poissons et de coquillages sont cultivées par différents types d'aquaculture. Ces élevages localisés près des côtes permettent d'augmenter la production d'une espèce de poisson en particulier.

Ce type d'exploitation permet de limiter la pêche industrielle en augmentant considérablement la production du stock dans les zones côtières. Les variations de prix influencent la pêche des populations naturelles, or les poissons issus de l'aquaculture sont en partie nourris grâce aux stocks sauvages. Ces deux types d'exploitation sont donc liés et l'aquaculture dépend de la pêche de stocks sauvages. Pour éviter ce problème, les poissons cultivés sont souvent de bas niveau trophique car leur régime alimentaire est de type herbivore et ne nécessitent donc pas d'être nourris par les poissons sauvages. L'aquaculture ne peut donc pas remplacer la pêche en pleine mer[10].

Les récifs artificiels sont aujourd'hui largement utilisés pour reconstituer un écosystème favorable à la réhabilitation de la faune et la flore aquatiques. Il s'agit d'un outil important pour la gestion des stocks de pêche car dans tous les cas, ce type d'aménagement augmente la densité de poissons et la biomasse. La taille des récifs et le type de matériaux utilisés permet d'attirer différentes espèces de poissons, mais surtout différentes classes d'âge.

En effet, aux États-Unis, les récifs recrutent des poissons adultes, alors qu'au Japon, les récifs artificiels sont construits de manière à attirer des juvéniles ainsi que des jeunes géniteurs. Les poissons étant regroupés autour d'une même structure, les récifs diminuent l'effort de pêche et maximisent les captures. On observe donc une augmentation de pêcheurs de loisir dans ces zones. Au Japon, les récifs artificiels sont très étendus et permettent une pêche commerciale à moindre coût, car l'effort de pêche est faible. Malgré une augmentation des stocks de poissons, ces récifs n'augmentent pas pour autant la production. La mise en place de ces structures ne doit cependant pas être à l'origine de nouvelles surexploitations des stocks, et nécessitent une gestion durable et efficace[11].