Courbe inverse

L'inverse du point (x, y) par rapport au cercle unité est (X, Y) où

${\displaystyle X={\frac {x}{x^{2}+y^{2}}},\qquad Y={\frac {y}{x^{2}+y^{2}}},}$

ou de façon équivalente

${\displaystyle x={\frac {X}{X^{2}+Y^{2}}},\qquad y={\frac {Y}{X^{2}+Y^{2}}}.}$

Ainsi, l'inverse de la courbe déterminée par f(x, y) = 0 par rapport au cercle unité est

${\displaystyle f\left({\frac {X}{X^{2}+Y^{2}}},{\frac {Y}{X^{2}+Y^{2}}}\right)=0.}$

Il en ressort clairement que l'inversion d'une courbe algébrique de degré n par rapport à un cercle génère une courbe algébrique de degré au plus 2n .

De même, l'inverse de la courbe définie par les équations paramétriques

${\displaystyle x=x(t),\qquad y=y(t)}$

par rapport au cercle unité est donné par

${\displaystyle {\begin{aligned}X=X(t)&={\frac {x(t)}{x(t)^{2}+y(t)^{2}}},\\Y=Y(t)&={\frac {y(t)}{x(t)^{2}+y(t)^{2}}}.\end{aligned}}}$

Cela implique que l'inverse circulaire d'une courbe rationnelle est également rationnelle.

Plus généralement, l'inverse de la courbe déterminée par f(x, y) = 0 par rapport au cercle de centre (a, b) et de rayon k est

${\displaystyle f\left(a+{\frac {k^{2}(X-a)}{(X-a)^{2}+(Y-b)^{2}}},b+{\frac {k^{2}(Y-b)}{(X-a)^{2}+(Y-b)^{2}}}\right)=0.}$

L'inverse de la courbe définie par ses équations paramétriques de la forme

${\displaystyle x=x(t),\qquad y=y(t)}$

par rapport au même cercle a pour équations paramétriques

${\displaystyle {\begin{aligned}X=X(t)&=a+{\frac {k^{2}\left(x(t)-a\right)}{\left(x(t)-a\right)^{2}+\left(y(t)-b\right)^{2}}},\\Y=Y(t)&=b+{\frac {k^{2}\left(y(t)-b\right)}{\left(x(t)-a\right)^{2}+\left(y(t)-b\right)^{2}}}.\end{aligned}}}$

En coordonnées polaires, les équations sont plus simples lorsque le cercle d'inversion est le cercle unité. L'inverse du point (r, θ) par rapport au cercle unitaire est (R, Θ) où

${\displaystyle R={\frac {1}{r}},\qquad \Theta =\theta .}$

Donc l'inverse de la courbe f(r, θ) = 0 est déterminé par f(1/R, Θ) = 0

Pour construire l'inverse P' d'un point P extérieur à un cercle Ø : Soit r le rayon de Ø. Les triangles rectangles OPN et ONP ' sont semblables. OP est à r ce que r est à OP '.

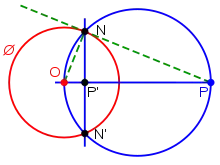
Pour construire le point inverse P' d'un point P par rapport à un cercle C de centre O et de rayon r, si le point est extérieur au cercle, on trace la tangente à C passant par P, puis on projette orthogonalement le point de tangence N sur la droite (OM). Ce point projeté est l'image de A' par inversion : en effet, on a, par similarité des triangles rectangles P'ON et NOP, l'égalité OP'×OP = P'N².

Comme indiqué ci-dessus, l'inverse par rapport à un cercle d'une courbe de degré n est de degré au plus 2n. Le degré est exactement 2n sauf si la courbe d'origine passe par le point d'inversion ou si elle est circulaire, ce qui signifie qu'elle contient les points circulaires, (1, ±i, 0), lorsqu'elle est considérée comme une courbe dans le plan projectif complexe. En général, l'inversion par rapport à une courbe arbitraire peut produire une courbe algébrique avec un degré proportionnellement plus grand.

Plus précisément, si C est p-circulaire de degré n, et si le centre d'inversion est une singularité d'ordre q sur C, alors la courbe inverse sera une courbe (n − p − q)-circulaire de degré 2n − 2p − q et le centre d'inversion est une singularité d'ordre n − 2p sur la courbe inverse. Ici q = 0 si la courbe ne contient pas le centre d'inversion et q = 1 si le centre d'inversion est un point non singulier sur celle-ci ; de même les points circulaires, (1, ±i, 0), sont des singularités d'ordre p sur C . La valeur k peut être éliminée de ces relations pour montrer que l'ensemble des p-courbes circulaires de degré p + k, où p peut varier mais k est un entier positif fixe, est invariant par inversion.

Pour une droite passant par l'origine, l'équation polaire est θ = θ₀ où θ₀ est fixe. Cela reste inchangé par inversion.

L'équation polaire d'une droite ne passant pas par l'origine est

${\displaystyle r\cos \left(\theta -\theta _{0}\right)=a}$

et l'équation de la courbe inverse est

${\displaystyle r=a\cos \left(\theta -\theta _{0}\right)}$

qui définit un cercle passant par l'origine. Plus précisément, ce cercle image est tel que la droite d'origine est l'axe radical des deux cercles (le cercle unité et le cercle image).

Une deuxième application de l'inversion montre que l'inverse d'un cercle passant par l'origine est une droite.

En coordonnées polaires, l'équation générale d'un cercle qui ne passe pas par l'origine (les autres cas ayant été traités) est

${\displaystyle r^{2}-2r_{0}r\cos \left(\theta -\theta _{0}\right)+r_{0}^{2}-a^{2}=0,\qquad (a>0,\ r>0,\ a\neq r_{0})}$

où a est le rayon et (r₀, θ₀) sont les coordonnées polaires du centre. L'équation de la courbe inverse est alors

${\displaystyle 1-2r_{0}r\cos \left(\theta -\theta _{0}\right)+\left(r_{0}^{2}-a^{2}\right)r^{2}=0,}$

ou

${\displaystyle r^{2}-{\frac {2r_{0}}{r_{0}^{2}-a^{2}}}r\cos \left(\theta -\theta _{0}\right)+{\frac {1}{r_{0}^{2}-a^{2}}}=0.}$

C'est l'équation d'un cercle de rayon

${\displaystyle A={\frac {a}{\left|r_{0}^{2}-a^{2}\right|}}}$

et de centre de coordonnées polaires

${\displaystyle \left(R_{0},\Theta _{0}\right)=\left({\frac {r_{0}}{r_{0}^{2}-a^{2}}},\theta _{0}\right).}$

On notera que R₀ peut être négatif.

Si le cercle d'origine coupe le cercle unité, alors les centres des deux cercles et un point d'intersection forment un triangle de côtés 1, a, r₀ ; c'est un triangle rectangle, c'est-à-dire que les rayons sont à angle droit, exactement quand

${\displaystyle r_{0}^{2}=a^{2}+1.}$

Mais d'après les équations ci-dessus, le cercle d'origine est le même que le cercle inverse exactement lorsque

${\displaystyle r_{0}^{2}-a^{2}=1.}$

Donc l'inverse d'un cercle est le même cercle si et seulement s'il coupe le cercle unité à angle droit.

Pour résumer et généraliser cette section et la précédente :

1. L'inverse d'une droite ou d'un cercle est une droite ou un cercle.
2. Si la courbe d'origine est une droite, la courbe inverse passera par le centre d'inversion. Si la courbe d'origine passe par le centre d'inversion, la courbe inversée sera une droite.
3. La courbe inversée sera la même que l'originale exactement lorsque la courbe coupe le cercle d'inversion à angle droit.

L'équation d'une parabole est, à similarité près, après translation pour que le sommet soit à l'origine et rotation pour que l'axe soit horizontal, x = y² . En coordonnées polaires cela devient

${\displaystyle r={\frac {\cos \theta }{\sin ^{2}\theta }}.}$

La courbe inverse a alors pour équation

${\displaystyle r={\frac {\sin ^{2}\theta }{\cos \theta }}=\sin \theta \tan \theta }$

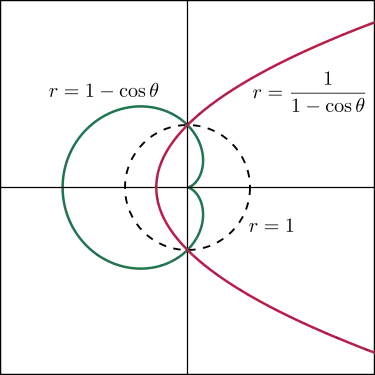
qui est la cissoïde de Dioclès.

L'équation polaire d'une section conique avec un foyer à l'origine est, à similarité près

${\displaystyle r={\frac {1}{1+e\cos \theta }},}$

où e est l'excentricité. L'inverse de cette courbe sera alors

${\displaystyle r=1+e\cos \theta ,}$

qui est l'équation d'un limaçon de Pascal. Lorsque e = 0, c'est le cercle d'inversion. Lorsque 0 < e < 1, la courbe d'origine est une ellipse et l'inverse est une simple courbe fermée avec un acnode à l'origine. Lorsque e = 1, la courbe d'origine est une parabole et l'inverse est la cardioïde qui a une pointe à l'origine. Lorsque e > 1 la courbe d'origine est une hyperbole et l'inverse forme deux boucles avec un crunode à l'origine.

L'équation générale d'une ellipse ou d'une hyperbole est

${\displaystyle {\frac {x^{2}}{a^{2}}}\pm {\frac {y^{2}}{b^{2}}}=1.}$

Après translation pour que l'origine soit à l'un des sommets, cela donne

${\displaystyle {\frac {(x-a)^{2}}{a^{2}}}\pm {\frac {y^{2}}{b^{2}}}=1}$

et le réarrangement donne

${\displaystyle {\frac {x^{2}}{2a}}\pm {\frac {ay^{2}}{2b^{2}}}=x}$

ou, en changeant les constantes,

${\displaystyle cx^{2}+dy^{2}=x.}$

On remarque alors que la parabole ci-dessus s'inscrit maintenant dans ce schéma en posant c = 0 et d = 1. L'équation de l'inverse est

${\displaystyle {\frac {cx^{2}}{\left(x^{2}+y^{2}\right)^{2}}}+{\frac {dy^{2}}{\left(x^{2}+y^{2}\right)^{2}}}={\frac {x}{x^{2}+y^{2}}}}$

ou

${\displaystyle x\left(x^{2}+y^{2}\right)=cx^{2}+dy^{2}.}$

Cette équation décrit une famille de courbes appelées les conchoïdes de de Sluze (en). Cette famille comprend, outre la cissoïde de Dioclès citée ci-dessus, la trisectrice de Maclaurin (d = −c/3) et la strophoïde droite (d = -c)

En inversant l'équation d'une ellipse ou d'une hyperbole

${\displaystyle cx^{2}+dy^{2}=1}$

on trouve

${\displaystyle \left(x^{2}+y^{2}\right)^{2}=cx^{2}+dy^{2}}$

qui est une hippopède. Lorsque d = −c c'est la lemniscate de Bernoulli.

En appliquant la formule des degrés ci-dessus, l'inverse d'une conique (autre qu'un cercle) est une cubique circulaire si le centre d'inversion est sur la courbe, et une quartique bicirculaire sinon. Les coniques sont rationnelles, donc les courbes inverses sont également rationnelles. Inversement, toute cubique circulaire rationnelle ou quartique bicirculaire rationnelle est l'inverse d'une conique. En fait, une telle courbe doit avoir une singularité réelle et en prenant ce point comme centre d'inversion, la courbe inverse sera une conique par la formule du degré[1] - [2].