Strophoïde
En mathématiques, et plus précisément en géométrie, une courbe strophoïdale, ou simplement une strophoïde, est une courbe engendrée à partir d'une courbe donnée C et de deux points A (le point fixe) et O (le pôle). Dans le cas particulier où C est une droite, A appartient à C, et O n'appartient pas à C, la courbe est appelée une strophoïde oblique. Si, de plus, OA est perpendiculaire à C, la courbe est appelée une strophoïde droite, ou simplement une strophoïde par certains auteurs. La strophoïde droite est aussi parfois appelée courbe logocyclique.
Construction
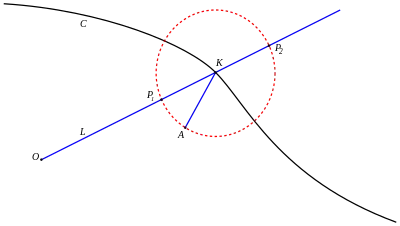
La courbe strophoïdale correspondant à la courbe C, au point fixe A et au pôle O est construite de la manière suivante : soit L une droite mobile passant par O et coupant C en K. Soit alors P1 et P2 les deux points de L tels que P1K = P2K = AK. Le lieu géométrique des pointsP1 et P2 est appelé la strophoïde de C relativement au pôle O et au point fixe A. On remarquera que AP1 et AP2 sont orthogonaux.
Équations
Coordonnées polaires
Soit la courbe C donnée par , où l'origine est prise en O. Soit A le point de coordonnées cartésiennes (a, b). Si est un point de la courbe, la distance de K à A est
- .
Les points de la droite OK ont pour angle polaire , et les points à distance d de K sur cette droite sont à une distance de l'origine. Par conséquent, l'équation de la strophoïde est donnée par
- .
Coordonnées cartésiennes
Soit C d'équations paramétriques (x=x(t),y= y(t)). Soit A le point (a, b) et O le point (p, q). Alors, les formules polaires précédentes montrent que la strophoïde est représentée paramétriquement par :
où
Une autre formule polaire
La complexité des formules précédentes limite leur utilité en pratique. Il en existe une forme alternative parfois plus simple, qui est particulièrement utile quand C est une sectrice de Maclaurin (en) de pôles O et A.
Soit O l'origine et A le point (a, 0). Soit K un point de la courbe, l'angle entre OK et l'axe Ox, et l'angle entre AK et l'axe Ox. Supposons que soit donné en fonction de , sous la forme . Soit l'angle en K, donc. On peut déterminer r en fonction de l en utilisant la loi des sinus : comme
- .
Soit P1 et P2 les points de la droite OK à distance AK de K, numérotés de façon que et . Le triangle est isocèle d'angle au sommet , donc les angles de la base, et , valent. L'angle entre AP1 et l'axe Ox est alors
- .
Utilisant le fait que AP1 et AP2 sont perpendiculaires (car le triangleAP1P2 est inscrit dans un demi-cercle), l'angle entre AP2 et l'axe Ox vaut
- .
L'équation polaire de la strophoïde se déduit alors de l1 et l2 d'après les formules précédentes :
C est une sectrice de Maclaurin de pôles O et A quand l est de la forme ; dans ce cas l1 et l2 ont la même forme, et la strophoïde est soit une autre sectrice de Maclaurin, soit un couple de sectrices ; on peut en trouver une équation polaire simple si on prend l'origine au symétrique de A par rapport àO.
Cas particuliers
Strophoïdes obliques
Soit C une droite passant par A. Alors, dans les notations précédentes, , où est une constante, et ; . Avec l'origine en O, les équations polaires de la strophoïde correspondante, appelée une strophoïde oblique deviennent
et
- .
On vérifie facilement que ces deux équations décrivent en fait la même courbe.
Déplaçant l'origine en A (voir, là encore, l'article sectrice de Maclaurin (en)) et remplaçant −a par a, on obtient
- ;
une rotation de transforme cette équation en
- .
En coordonnées cartésiennes (et en changeant les constantes), on obtient
- .
C'est une cubique, unicursale d'après l'équation polaire. Elle possède un point double en (0, 0), et la droite y=b lui est asymptote.
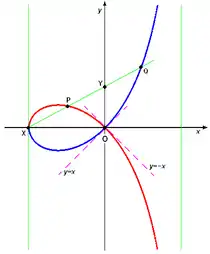
La strophoïde droite
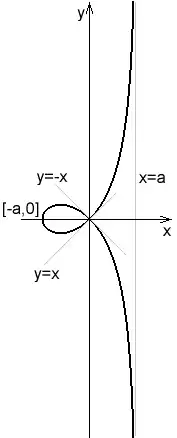
Posant dans
- ,
on obtient
- .
Cette courbe est appelée la strophoïde droite, et correspond au cas où C est l'axe Oy, O est l'origine, et A est le point (a,0).
L'équation cartésienne est
- ;
une représentation paramétrique unicursale est :
- .
La courbe ressemble au folium de Descartes, et la droite x = −a est asymptote aux deux branches infinies. La courbe possède deux autres asymptotes "imaginaires" dans le plan complexifié , données par
- .
Strophoïdes de cercles passant par les points fixes
Soit C un cercle passant par O et A. Prenant O pour origine et A en (a, 0), on obtient, dans les notations précédentes, , où est une constante. Ainsi, et . Les équations polaires des strophoïdes correspondantes sont alors
et
- .
Ce sont les équations de deux cercles passant également par O et A, et formant des angles de avec C en ces points.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Strophoid » (voir la liste des auteurs).
- Sur le site de Robert Ferréol, dans son encyclopédie des formes mathématiques remarquables :
- "Courbe Strophoïdale" ,
- "Strophoïde" ,
- "Strophoïde Droite", où l'on trouvera également beaucoup de propriétés géométriques de cette courbe ;
- Sur le site de MathWorld :
- (en) Eric W. Weisstein, « Strophoid », sur MathWorld,
- (en) Eric W. Weisstein, « Right Strophoid », sur MathWorld.













































