Calcul du volume de l'hypersphère

Notons ${\displaystyle V^{(n)}[r]}$ le volume de la boule de rayon r en dimension n ≥ 1. Alors :

${\displaystyle V^{(1)}[r]=2r}$

parce que c'est la longueur d'un segment deux fois plus long que le rayon, i.e.

${\displaystyle \{x\in \mathbb {R}$ :|x|\leq r\}=[-r,r].}

La sphère de dimension 0 qui borde cette boule est constituée des deux points r et –r.

Pour tout n ≥ 1 nous avons (d'après le théorème de Fubini)[1] :

${\displaystyle V^{(n+1)}[r]=\int _{-r}^{r}V^{(n)}\left[{\sqrt {r^{2}-x^{2}}}\,\right]~{\rm {d}}x.}$

Nous montrerons premièrement par récurrence sur n que le volume d'une n-boule est proportionnel à la n-ième puissance de son rayon. Nous avons déjà observé que c'est vrai en dimension 1. Supposons maintenant que ce soit vrai en dimension n, i.e. :

${\displaystyle V^{(n)}[r]=r^{n}V^{(n)}[1].}$

Alors,

${\displaystyle {\begin{aligned}V^{(n+1)}[r]&=\int _{-r}^{r}V^{(n)}\left[{\sqrt {r^{2}-x^{2}}}\,\right]~{\rm {d}}x\\&=r\int _{-1}^{1}V^{(n)}\left[{\sqrt {r^{2}-(rx)^{2}}}\,\right]~{\rm {d}}x\\&=r\int _{-1}^{1}V^{(n)}\left[r{\sqrt {(1-x^{2})}}\,\right]~{\rm {d}}x\\&=r\int _{-1}^{1}r^{n}V^{(n)}\left[{\sqrt {(1-x^{2})}}\,\right]~{\rm {d}}x\\&=r^{n+1}V^{(n+1)}[1].\end{aligned}}}$

Nous avons établi que pour tout n ≥ 1, le volume d'une n-boule est proportionnel à la n-ième puissance de son rayon ; c'est-à-dire que si nous notons ${\displaystyle V^{(n)}[1]}$ le volume de la n-boule unitaire, nous avons :

${\displaystyle V^{(n)}[r]=r^{n}V^{(n)}[1],}$

${\displaystyle V^{(n+1)}[1]=\int _{-1}^{1}\left({\sqrt {1-x^{2}}}\,\right)^{n}V^{(n)}[1]~{\rm {d}}x=V^{(n)}[1]\int _{-1}^{1}\left({\sqrt {1-x^{2}}}\,\right)^{n}~{\rm {d}}x.}$

Dans le cas de ${\displaystyle V^{(2)}[1]}$ nous avons[2] :

${\displaystyle V^{(2)}[1]=V^{(1)}[1]\int _{-1}^{1}{\sqrt {1-x^{2}}}~{\rm {d}}x=2\left.{\frac {x{\sqrt {1-x^{2}}}+\arcsin x}{2}}\right|_{x=-1}^{1}=\pi ,}$

qui est « l'aire intérieure du cercle unité », ou plus exactement, l'aire du disque borné par ce cercle. On en déduit facilement :

${\displaystyle V^{(3)}[1]=V^{(2)}[1]\int _{-1}^{1}\left(1-x^{2}\right)~{\rm {d}}x={\frac {4}{3}}\pi .}$

Ceci est « le volume intérieur de la sphère unité », ou plus exactement, le volume de la boule délimitée par cette sphère.

Essayons maintenant de généraliser cette démonstration au cas de la boule en dimension supérieure :

${\displaystyle V^{(n+1)}[1]=V^{(n)}[1]\int _{-1}^{1}\left(1-x^{2}\right)^{n/2}~{\rm {d}}x=V^{(n)}[1]\cdot 2\int _{0}^{1}\left(1-x^{2}\right)^{n/2}~{\rm {d}}x.}$

Voici un graphe de la fonction que nous avons intégrée ici, pour rendre plus facile la visualisation de cette fonction dans plusieurs dimensions :

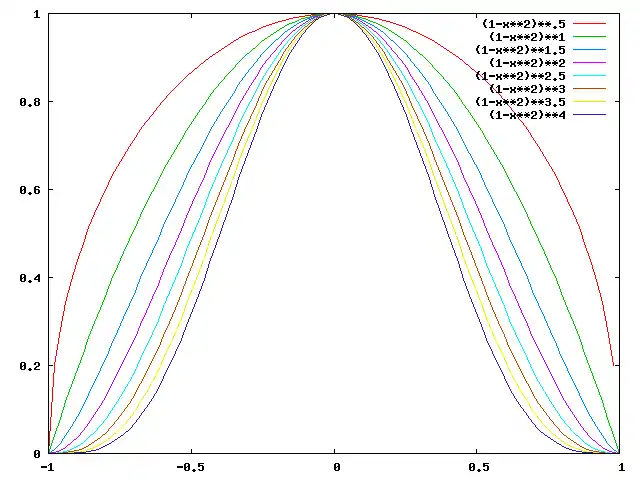
Les hyperboules se pincent de plus en plus comme la dimension croît. (Plus précisément, puisque nous intégrons en coordonnées rectangulaires, et que les boîtes rectangulaires circonscrites aux boules s'étendent de plus en plus hors des boules comme la dimension croît, les boules nous paraissent de plus en plus pincées au point de vue des coordonnées dans lesquelles nous intégrons.)

Par le changement de variables ${\displaystyle u=x^{2}}$ nous avons :

${\displaystyle x={\sqrt {u}}\qquad {\text{et}}\qquad {\rm {d}}x={\frac {{\rm {d}}u}{2{\sqrt {u}}}}}$

${\displaystyle V^{(n+1)}[1]=V^{(n)}[1]~2\int _{0}^{1}\left(1-x^{2}\right)^{n/2}~{\rm {d}}x=V^{(n)}[1]\int _{0}^{1}(1-u)^{n/2}u^{-1/2}~{\rm {d}}u.}$

L'intégrale à droite est connue comme la fonction bêta :

${\displaystyle V^{(n+1)}[1]=V^{(n)}[1]~\mathrm {B} \left({\frac {n}{2}}+1,{\frac {1}{2}}\right),}$

qui peut être exprimée au moyen de la fonction gamma :

${\displaystyle V^{(n+1)}[1]=V^{(n)}[1]{\frac {\Gamma \left({\frac {n}{2}}+1\right)\Gamma \left({\frac {1}{2}}\right)}{\Gamma \left({\frac {n}{2}}+{\frac {3}{2}}\right)}}.}$

À partir de la relation ${\displaystyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }},}$ nous pouvons facilement vérifier par récurrence que pour tout n ≥ 1,

${\displaystyle V^{(n)}[1]={\frac {\pi ^{n/2}}{\Gamma \left({\frac {n}{2}}+1\right)}}.}$

Et donc finalement, pour un rayon ${\displaystyle r}$ on aura

${\displaystyle V^{(n)}[r]={\frac {\pi ^{n/2}r^{n}}{\Gamma \left({\frac {n}{2}}+1\right)}}={\begin{cases}{\frac {\pi ^{n/2}r^{n}}{(n/2)!}}&{\mbox{si }}n{\mbox{ est pair,}}\\{\frac {2^{n}\ ({\frac {n-1}{2}})!\ \pi ^{(n-1)/2}r^{n}}{n!}}={\frac {2^{(n+1)/2}\ \pi ^{(n-1)/2}r^{n}}{1.3.5.\ \ldots n}}&{\mbox{si }}n{\mbox{ est impair.}}\end{cases}}}$

Par « désintégration de mesure »[3], l'aire de l'hypersphère de dimension n – 1 est la dérivée, par rapport à son rayon, du volume de la boule de dimension n qu'elle borde.

Puisque le volume de la boule de dimension n est :

${\displaystyle V^{(n)}[r]={\frac {\pi ^{n/2}r^{n}}{\Gamma \left({\frac {n}{2}}+1\right)}},}$

alors l'aire de l'hypersphère de dimension n – 1 qui la borde est :

${\displaystyle S^{(n-1)}[r]={\frac {\partial }{\partial r}}V^{(n)}[r]={\frac {\pi ^{n/2}nr^{n-1}}{\Gamma \left({\frac {n}{2}}+1\right)}}={\frac {n}{r}}.V^{(n)}[r]}$.

Et comme ${\displaystyle {\Gamma \left({\frac {n}{2}}+1\right)}={\frac {n}{2}}{\Gamma \left({\frac {n}{2}}\right)}}$ on peut écrire aussi :

${\displaystyle S^{(n-1)}[r]={\frac {2\pi ^{n/2}r^{n-1}}{\Gamma \left({\frac {n}{2}}\right)}}.}$

À partir de la récurrence d'ordre 1 :

${\displaystyle V^{(n+1)}[1]=V^{(n)}[1]~\mathrm {B} \left({\frac {n}{2}}+1,{\frac {1}{2}}\right),~}$

utilisée plus haut directement pour exprimer V⁽ⁿ⁾ en termes de la fonction gamma, une alternative est d'écrire une récurrence d'ordre 2 :

${\displaystyle V^{(n)}[1]=V^{(n-2)}[1]~\mathrm {B} \left({\frac {n+1}{2}},{\frac {1}{2}}\right)\mathrm {B} \left({\frac {n}{2}},{\frac {1}{2}}\right)~}$

qui, d'après les propriétés de la fonction bêta, se simplifie en :

${\displaystyle V^{(n)}[1]={\frac {2\pi }{n}}~V^{(n-2)}[1].}$

Par récurrence (en séparant les cas n pair et impair), on retrouve alors la formule donnée précédemment, qui peut aussi s'écrire :

${\displaystyle V^{(n)}[1]={\begin{cases}\prod _{k=0}^{{\frac {n}{2}}-1}{2\pi \over n-2k}&{\mbox{si }}n{\mbox{ est pair,}}\\{\frac {1}{\pi }}\prod _{k=0}^{n-1 \over 2}{2\pi \over n-2k}&{\mbox{si }}n{\mbox{ est impair.}}\end{cases}}}$

Par ailleurs, une manière plus directe[4] de démontrer cette formule de récurrence d'ordre 2 est de procéder comme pour celle d'ordre 1 :

${\displaystyle V^{(n)}[1]=\int _{x^{2}+y^{2}\leq 1}V^{(n-2)}[{\sqrt {1-x^{2}-y^{2}}}]~\mathrm {d} x\mathrm {d} y=V^{(n-2)}[1]\int _{x^{2}+y^{2}\leq 1}(1-x^{2}-y^{2})^{(n-2)/2}~\mathrm {d} x\mathrm {d} y={\frac {2\pi }{n}}~V^{(n-2)}[1],}$

la dernière égalité venant du passage en coordonnées polaires :

${\displaystyle \int _{x^{2}+y^{2}\leq 1}(1-x^{2}-y^{2})^{(n-2)/2}~\mathrm {d} x\mathrm {d} y=2\pi \int _{0}^{1}(1-r^{2})^{(n-2)/2}~r~\mathrm {d} r=\pi \int _{0}^{1}u^{(n/2)-1}~\mathrm {d} u={\frac {2\pi }{n}}.}$

• Empilement compact
• Code parfait et code MDS
• Intégrale de Wallis

• Démonstration en coordonnées hypersphériques
• (en) Eric W. Weisstein, « Hypersphere », sur MathWorld
• (en) Integral Calculus, The Volume of the Hypersphere