Attracteur de Lorenz
L’attracteur de Lorenz est une structure fractale correspondant au comportement à long terme de l'oscillateur de Lorenz. L'attracteur montre comment les différentes variables du système dynamique évoluent dans le temps en une trajectoire non périodique.

En 1963, le météorologue Edward Lorenz est le premier à mettre en évidence le caractère vraisemblablement chaotique de la météorologie. Le modèle de Lorenz, appelé aussi système dynamique de Lorenz ou oscillateur de Lorenz, est une modélisation simplifiée de phénomènes météorologiques basée sur la mécanique des fluides. Ce modèle est un système dynamique tridimensionnel qui engendre un comportement chaotique dans certaines conditions.
Le modèle de Lorenz a eu des répercussions importantes en montrant les limites possibles sur la capacité de prédiction à long terme de l'évolution climatique et météorologique. C'est un élément important de la théorie selon laquelle l'atmosphère des planètes et des étoiles peut comporter une grande variété de régimes quasi périodiques et est sujette à des changements abrupts et, en apparence, aléatoires. C'est aussi un exemple utile à la théorie des systèmes dynamiques servant de source à de nouveaux concepts mathématiques[1].
Modèle de Lorenz
L'attracteur et les équations associées ont été rendues publiques en 1963 par Edward Lorenz.
Mathématiquement, le couplage de l'atmosphère terrestre avec l'océan est décrit par le système d'équations aux dérivées partielles couplées de Navier-Stokes de la mécanique des fluides. Ce système d'équations était beaucoup trop compliqué à résoudre numériquement pour les ordinateurs existant au temps de Lorenz. Celui-ci eut donc l'idée de chercher un modèle très simplifié de ces équations pour étudier une situation physique particulière : le phénomène de convection de Rayleigh-Bénard. Il aboutit alors à un système dynamique différentiel possédant seulement trois degrés de liberté, beaucoup plus simple à intégrer numériquement que les équations de départ.
Système dynamique différentiel de Lorenz
Ce système différentiel s'écrit :
où σ, ρ et β sont trois paramètres strictement positifs, fixés. Le système provenant de la simplification des équations régissant la convection de Rayleigh-Bénard, les paramètres sont dénommés d'après leur origine physique : σ est le nombre de Prandtl, et ρ, abusivement dénommé « nombre de Rayleigh », est en fait le rapport du nombre de Rayleigh Ra au nombre de Rayleigh critique Rac (Rac est la valeur de Ra au-dessus de laquelle le système physique ne peut pas rester invariant au cours du temps, où donc il est sujet à des mouvements de convection).
Les variables dynamiques x, y et z représentent l'état du système à chaque instant. L'interprétation physique en est la suivante : x(t) est proportionnel à l'intensité du mouvement de convection, y(t) est proportionnel à la différence de température entre les courants ascendants et descendants, et z(t) est proportionnel à l'écart du profil de température vertical par rapport à un profil linéaire[2].
On pose souvent σ = 10 et β = 8/3, ρ restant variable. Le système présente un comportement chaotique pour ρ = 28, après un certain temps en régime pseudo-périodique (de l'ordre de 30 secondes). Cette durée dépend de ρ : elle peut monter à 180 secondes pour ρ = 24,3. Le seuil d'établissement du régime chaotique se situe entre 24,29 et 24,30 pour ces valeurs de σ et β[3].
Points d'équilibre
Les points d'équilibre, ou points fixes, du système sont les solutions (x,y,z) constantes du système différentiel. Il en existe un ou trois :
- le point fixe (0, 0, 0) existe quelles que soient les valeurs des paramètres réels σ, ρ et β. Il est stable quand (convergence vers l'état de repos, pas de convection), instable dans le cas contraire (convection) ;
- les deux points fixes symétriques et n'existent que pour . Selon les valeurs de σ et ρ, ils sont stables (convection stationnaire) ou instables (convection fluctuant périodiquement, ou bien chaotique).
Description
L'attracteur de Lorenz est défini comme l'ensemble des trajectoires à long terme du système dynamique de Lorenz ci-dessus.
En effet lorsque les paramètres σ, ρ et β prennent les valeurs suivantes : σ = 10, ρ = 28 et β = 8/3, le système dynamique différentiel de Lorenz présente un attracteur étrange en forme d'ailes de papillon, représenté sur la figure ci-contre.
Pour presque toutes les conditions initiales (différentes de celles des points fixes), l'orbite du système s'approche rapidement de l'attracteur, la trajectoire commençant par s'enrouler sur une aile, puis sautant d'une aile à l'autre pour commencer à s'enrouler sur l'autre aile, et ainsi de suite, de façon apparemment erratique.
L'existence d'un attracteur étrange pour certaines valeurs des paramètres a été conjecturée par Edward Lorenz dès 1963 sur la base de simulations numériques. Il a cependant fallu attendre 2001 pour avoir une démonstration rigoureuse de ce fait par Warwick Tucker[4].
L'attracteur, dans ces cas, est une fractale de dimension de Hausdorff comprise entre 2 et 3[5].
 ρ = 28, σ = 10, β = 8/3
ρ = 28, σ = 10, β = 8/3
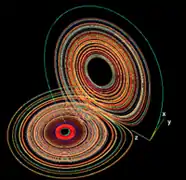 ρ = 28
ρ = 28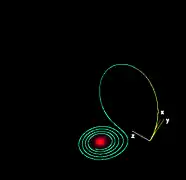 ρ = 15
ρ = 15 Animation de ρ = 0 à 28
Animation de ρ = 0 à 28
Variantes
Afin d'étudier mathématiquement l'attracteur de Lorenz des modèles rigoureux mais distincts de celui-ci sont apparus dans la littérature scientifique[6]. Leur intérêt principal étant qu'ils étaient plus faciles à étudier et surtout on était sûr de leur existence (néanmoins on ignorait si l'attracteur de Lorenz était correctement décrit par ces modèles, voir plus haut).
Notes et références
- Ghys 2010.
- Tels que définis dans Lorenz 1963, p. 135.
- La valeur du seuil peut dépendre des paramètres de résolution numérique du système.
- Tucker 2002.
- (en) P. Grassberger et I. Procaccia, « Measuring the strangeness of strange attractors », Physica D, vol. 9, nos 1-2, , p. 189-208 (DOI 10.1016/0167-2789(83)90298-1, Bibcode 1983PhyD....9..189G) ont estimé sa valeur à 2,06 ± 0,01 et sa dimension de corrélation à 2,05 ± 0,01.
- Appelés « modèles géométriques de Lorenz », cf. Afraimovich, Bykov et Shil’nikov 1977 et Guckenheimer et Williams 1979.
Voir aussi
Bibliographie
- (en) Edward N. Lorenz, « Deterministic nonperiodic flow », J. Atmos. Sci., vol. 20, no 2, , p. 130-141 (DOI 10.1175/1520-0469(1963)020%3c0130:DNF%3e2.0.CO;2, lire en ligne)
- (ru) V. S. Afraimovich, V. V. Bykov et L. P. Shil’nikov, « The origin and structure of the Lorenz attractor », Dokl. Akad. Nauk SSSR, vol. 234, t. 2, , p. 336-339.
- (en) J. Guckenheimer et R. F. Williams, « Structural stability of Lorenz attractors », Inst. Hautes études Sci. Publ. Math., vol. 50, , p. 59-72.
- (en) W. Tucker, « A Rigorous ODE Solver and Smale's 14th Problem », Foundations of Computational Mathematics, vol. 2, , p. 53-117 (lire en ligne).
- (en) R. F. Williams, « The structure of Lorenz attractors », Inst. Hautes études Sci. Publ. Math., vol. 50, , p. 73-99
- Étienne Ghys, « L'attracteur de Lorenz, paradigme du chaos », dans Séminaire Poincaré, vol. XIV, , 1-52 p. (lire en ligne [PDF])
![{\displaystyle {\begin{cases}{\dfrac {\mathrm {d} x}{\mathrm {d} t}}=\sigma \left[y(t)-x(t)\right]\\{\dfrac {\mathrm {d} y}{\mathrm {d} t}}=\rho \,x(t)-y(t)-x(t)\,z(t)\\{\dfrac {\mathrm {d} z}{\mathrm {d} t}}=x(t)\,y(t)-\beta \,z(t)\end{cases}}}](https://img.franco.wiki/i/331948ae59585ec8f0e4c8d8da03faa94f04d287.svg)



