Astuce du noyau

En apprentissage automatique, l'astuce du noyau, ou kernel trick en anglais, est une méthode qui permet d'utiliser un classifieur linéaire pour résoudre un problème non linéaire. L'idée est de transformer l'espace de représentation des données d'entrées en un espace de plus grande dimension, où un classifieur linéaire peut être utilisé et obtenir de bonnes performances. La discrimination linéaire dans l'espace de grande dimension (appelé aussi espace de redescription) est équivalente à une discrimination non linéaire dans l'espace d'origine.

Principe

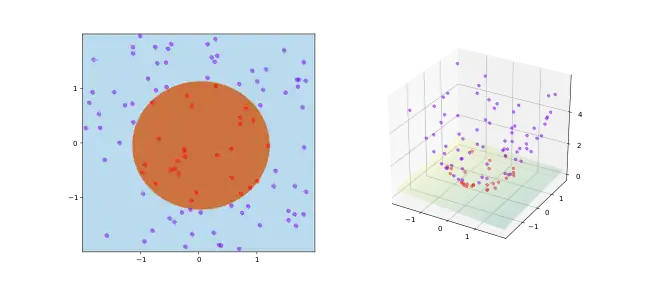
Principe du noyau pour apprendre si un point est dans un disque ou non.

A partir des coordonnées d'un point (x, y) dans le plan, impossible de dire s'il est dans le disque orange de rayon 1 ou non, en disant s'il est à gauche ou droite d'une droite du plan. Par contre, si on ajoute $x^{2}+y^{2}$ comme une troisième coordonnée, le point devient $(x,y,x^{2}+y^{2})$ dans un espace à trois dimensions. On peut affirmer qu'un point se trouve dans le disque s'il est en dessous du plan $x^{2}+y^{2}=1$ , c'est-à-dire si $x^{2}+y^{2}\leq 1$ .

Description

Contexte et principe

L'astuce du noyau s'utilise dans un algorithme qui ne dépend que du produit scalaire entre deux vecteurs d'entrée x et y. Après passage à un espace de redescription par une transformation $φ$ , l'algorithme n'est plus dépendant que du produit scalaire :

\varphi (x)\cdot \varphi (y)

Le problème de ce produit scalaire est qu'il est effectué dans un espace de grande dimension, ce qui conduit à des calculs impraticables. L'idée est donc de remplacer ce calcul par une fonction noyau de la forme :

K(x,y)=\varphi (x)\cdot \varphi (y).

Théorème de Mercer

Pour réaliser cela, on utilise le théorème de Mercer, qui montre qu'une fonction noyau K continue, symétrique et semi-définie positive peut s'exprimer comme un produit scalaire dans un espace de grande dimension.

Plus précisément, si les arguments de la fonction noyau sont à valeurs dans un espace mesurable X, et si le noyau est semi-défini positif — i. e.

\sum _{i,j}K(x_{i},x_{j})c_{i}c_{j}\geq 0

pour tout sous-ensemble {x₁, …, x_n} de X, et sous-ensemble {c₁, …, c_n} d'objets (en général des réels) —, alors il existe une fonction $φ$ dont l'image correspond à un espace préhilbertien possiblement de plus grande dimension tel que :

K(x,y)=\varphi (x)\cdot \varphi (y).

Mise en place et avantages

L'astuce du noyau consiste donc à remplacer un produit scalaire dans un espace de grande dimension par une fonction noyau, facile à calculer. De cette manière, un classifieur linéaire peut facilement être transformé en un classifieur non linéaire. Un autre avantage des fonctions noyau est qu'il n'est pas nécessaire d'expliciter la transformation $φ$ . Celle-ci peut même transformer l'espace d'entrée en un espace de redescription infini, comme le noyau gaussien :

K(\mathbf {x} ,\mathbf {y} )=\exp \left(-{\frac {\|\mathbf {x} -\mathbf {y} \|^{2}}{2\sigma ^{2}}}\right).

Applications

Après avoir été longuement négligée après la publication d'Aizerman de 1964, l'astuce du noyau a été popularisée par Boser et al. dans leur papier fondateur sur les machines à vecteurs de support[1]. L'idée a depuis été appliquée à plusieurs types d'algorithmes en apprentissage automatique et en statistiques :

Exemple de modification de l'espace de description de données grâce à une fonction kernel polynomiale pour maximiser la variance d'une Analyse en composantes principales

Histoire

L'astuce du noyau a été publiée en 1964 par Aizerman et al.[2]

Références

(en) Bernhard E. Boser, Isabelle Guyon et Vladimir Vapnik, « A Training Algorithm for Optimal Margin Classifiers », dans Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, ACM, 1992, p. 144-152.
(en) M. Aizerman, E. Braverman et L. Rozonoer, « Theoretical foundations of the potential function method in pattern recognition learning », Automation and Remote Control, vol. 25,‎ 1964, p. 821-837.

Voir aussi

Bibliographie

(en) Bernhard Schölkopf et Alexander J. Smola, Learning With Kernels: Support Vector Machines, Regularization, Optimization and Beyond, MIT Press, 2002

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.