Noyau (statistiques)

Un noyau est une fonction de pondération utilisée dans les techniques d'estimation non-paramétrique. Les noyaux interviennent dans l'estimateur par noyau pour estimer la densité de probabilité d'une variable aléatoire, ou encore dans la régression paramétrique (à noyau) pour estimer des espérances conditionnelles. Pour les séries temporelles, le noyau permet d'estimer la densité spectrale.

Définition

Un noyau est une fonction positive, intégrable et à valeurs réelles, notée $K$ , qui doit vérifier les deux conditions suivantes :

normalisation : $\int _{-\infty }^{+\infty }K(u)du=1\,;$
symétrie : $K(-u)=K(u)$ pour toutes les valeurs de $u$ .

La première condition assure que l'estimation à noyau soit bien une densité de probabilité, la seconde assure que l'espérance de l'estimateur est égale à celle de la fonction estimée.

Si $K$ est un noyau, alors il en ira de même pour $K * = 1 / λ K (u / λ)$ , où $λ > 0$ . Cette méthode permet de choisir une échelle adaptée aux données.

Les différents noyaux courants

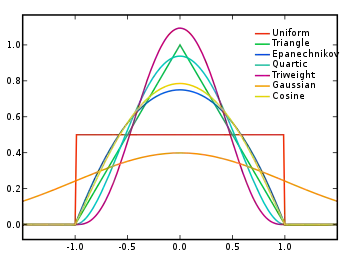
Plusieurs types de noyaux sont couramment utilisés : uniforme, triangle, d'Epanechnikov, quadratique, cubique, gaussien, et circulaire.

Ci-dessous, on note $1_{(p)}\,\!$ la fonction indicatrice qui vaut 1 lorsque p est vrai, 0 sinon.

Tous les noyaux évoqués représentés dans le système de coordonnées usuel.

Uniforme

La forme du noyau est une fonction porte :

K(u)={\frac {1}{2}}\ 1_{(|u|\leq 1)}

La fonction estimée aura alors la forme d'un histogramme et n'aura d'intérêt que pour avoir une première estimation de la forme du modèle lisse.

Triangle

La forme du noyau est une fonction triangulaire :

K(u)=(1-|u|)\ 1_{(|u|\leq 1)}

La fonction estimée sera alors linéaire par morceaux.

Epanechnikov

On parle aussi de noyau « parabolique ». Il porte le nom de V.A. Epanechnikov, qui l'a utilisé et étudié pour la première fois en 1969[1] :

K(u)={\frac {3}{4}}(1-u^{2})\ 1_{(|u|\leq 1)}

Ce noyau permet d'avoir l'estimateur le plus efficace pour la densité.

Quartique

K(u)={\frac {15}{16}}(1-u^{2})^{2}\ 1_{(|u|\leq 1)}

Cubique

K(u)={\frac {35}{32}}(1-u^{2})^{3}\ 1_{(|u|\leq 1)}

Gaussien

K(u)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}u^{2}}

Circulaire

K(u)={\frac {\pi }{4}}\cos \left({\frac {\pi }{2}}u\right)1_{(|u|\leq 1)}

Voir aussi

Estimateur par noyau

Références

(en) V. A. Epanechnikov, « Non-Parametric Estimation of a Multivariate Probability Density », Theory Probab. Appl., vol. 14, n^o 1,‎ 1969, p. 153–158 (DOI 10.1137/1114019)

Liens externes

Kernel Basis function.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.