Fonction triangulaire
Une fonction triangulaire (ou fonction triangle, fonction chapeau ou fonction tente) est une fonction dont la représentation graphique est un triangle. Souvent, c'est un triangle isocèle de hauteur 1 et de base 2 et dans ce cas, on s'y réfère comme la fonction triangulaire. Les fonctions triangulaires sont utiles en traitement du signal et en génie des systèmes de communication comme représentations idéalisées des signaux, et particulièrement la fonction triangulaire comme un opérateur intégral de noyau à partir de laquelle des signaux plus réalistes peuvent être dérivés, par exemple dans l'estimation de densités de noyaux. Elle a également des applications en modulation d'impulsion codée sous la forme d'une impulsion pour la transmission de signaux logiques et en tant que filtre adapté (en) pour recevoir les signaux. Elle est également utilisé pour définir la fenêtre triangulaire parfois appelée la fenêtre de Bartlett.
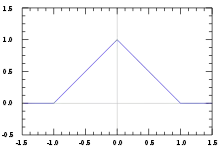
Définitions
La définition la plus commune est une fonction affine par morceaux :
De façon équivalents, la fonction triangulaire peut être définie comme la fonction d'auto-convolution de la fonction porte :
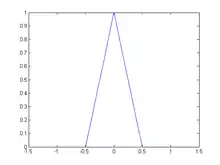
Certains auteurs utilisent une définition de la fonction triangulaire de largeur 1 au lieu de 2 :
Dans sa forme la plus générale, une fonction triangulaire est une B-spline linéaire[1]:
La première définition donnée est un cas particulier :
avec xj–1 = –1, xj = 0 et xj+1 = 1.
Échelle
Pour tout paramètre :
Transformée de Fourier
Grâce aux propriétés de la transformation de Fourier sur la convolution, le calcul montre que la transformée de Fourier de la fonction triangulaire est le carré de celle de la fonction porte :
où sinc désige ici la fonction sinus cardinal normalisée sinc(x) = sin(π x) / (π x).
Voir aussi
- Fonction de Källén, une fonction triangulaire définie sur R3
- Loi triangulaire et loi d'Irwin-Hall
- Signal triangulaire
- Fonction trigonométrique
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Triangular function » (voir la liste des auteurs).
- (en) INF-MAT5340 Lecture Notes (lire en ligne), « Basic properties of splines and B-splines », p. 38
![{\displaystyle {\begin{aligned}\operatorname {tri} (x)=\Lambda (x)\ &{\overset {\underset {\mathrm {def} }{}}{=}}\ \max(1-|x|,0)\\[3pt]&={\begin{cases}1-|x|\quad &{\text{si }}|x|<1\\0\quad &{\text{sinon}}\\\end{cases}}\\[3pt]&=\Pi (x/2)\left(1-|x|\right)\end{aligned}}}](https://img.franco.wiki/i/5ef90f657f4ca1e34fa60b31bc15d297c1d720ca.svg)

![{\displaystyle {\begin{aligned}\operatorname {tri} (2x)=\Lambda (2x)\ &{\overset {\underset {\text{def}}{}}{=}}\ \max \left(1-2|x|,0\right)\\[3pt]&={\begin{cases}1-2|x|,&{\text{si }}|x|<{\tfrac {1}{2}};\\0&{\text{sinon}}.\\\end{cases}}\\[3pt]&=\Pi (x)\left(1-2|x|\right)\end{aligned}}}](https://img.franco.wiki/i/b1ab5a9e78b395dfff43258ad5d8aa02a8b2cca5.svg)
![{\displaystyle \operatorname {tri} _{j}(x)={\begin{cases}{\tfrac {x-x_{j-1}}{x_{j}-x_{j-1}}},&{\text{si }}x_{j-1}\leq x<x_{j};\\[6pt]{\tfrac {x_{j+1}-x}{x_{j+1}-x_{j}}},&{\text{si }}x_{j}\leq x<x_{j+1};\\[6pt]0&{\text{sinon}}.\end{cases}}}](https://img.franco.wiki/i/d25dcec3a287c6d697e7d6d1ef2c8a567db32286.svg)



