Fonction affine par morceaux

La fonction valeur absolue est une fonction affine par morceaux définie sur ℝ par :

• |x|= -x si x < 0
• |x|= x si x ≥ 0

De même, la fonction définie par f(x)= |x - 3| + 2|x + 5| est une fonction affine par morceaux ainsi que la fonction partie entière de x, non seulement affine par morceaux mais constante par morceaux.

On peut également citer la fonction partie fractionnaire et la fonction de Heaviside comme exemples de fonctions affines par morceaux.

Courbe représentative de la fonction définie ci-contre.

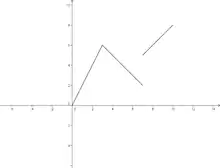
Un des problèmes posé par la construction d’une fonction affine par morceaux est la présence ou non de saut. Si les segments de droites sont jointifs, la représentation graphique forme une ligne polygonale. Une petite variation sur la variable entraine une petite variation sur f(x). C’est l’approche intuitive de ce que l’on appelle en mathématique la continuité.

Exemple : la première fonction donnée était définie par :

${\displaystyle f(x)=\left\{{\begin{array}{cl}2\ x&\mathrm {si} \ x\in [0;3];\\9-x&\mathrm {si} \ x\in [3;7[;\\x-2&\mathrm {si} \ x\in [7;10]\end{array}}\right.}$

Elle est bien continue en 3 car, si x s’approche de 3 en restant inférieur à 3, alors la valeur de f(x) s’approche de 6 (= 2 × 3) et quand x s’approche de 3 par valeur supérieure la valeur de f(x) s’approche de 6 (= 9 - 3).

En revanche, elle n’est pas continue en 7, car si x s’approche de 7 en restant inférieur à 7, alors f(x) s’approche de 2, tandis que si x s’approche de 7 en restant supérieur à 7, alors f(x) s’approche de 5.

Cet exemple est tiré de l'impôt sur le revenu des personnes physiques en France en 2006 qui donne le montant de l’impôt en fonction du quotient familial (revenu annuel après déduction divisé par nombre de part). Pour simplifier, on prendra comme exemple un célibataire (nombre de part = 1). Si le revenu est R, alors l'impôt I est calculé par :

Impots en fonction du revenu imposable - Unités milliers d'euros

• si R < 4412 alors I = 0
• si R ${\displaystyle \in }$ [4412 ; 8677] alors I = R × 0,0683 - 301,84
• si R ${\displaystyle \in }$ ]8677 ; 15274] alors I = R × 0,1914 - 1369,48
• si R ${\displaystyle \in }$ ]15274 ; 24731] alors I = R × 0,2826 - 2762,47
• si R ${\displaystyle \in }$ ]24731 ; 40241] alors I = R × 0,3738 - 5017,93
• si R ${\displaystyle \in }$ ]40241 ; 49624] alors I = R × 0,4262 - 7126,56
• si R > 49624 alors I = R × 0,4809 - 9841

Ceci représente une fonction affine par morceaux. Changer de tranche, c'est changer de fonction affine. Le taux d'imposition y est plus élevé. Est-ce pour autant que le changement entraine un saut significatif dans l'impôt ?

Un rapide calcul pour un revenu de 15273 et un revenu de 15275 euros (changement de tranche) donne, pour le premier cas, un impôt de 1553,77 euros et, dans le second cas, un impôt de 1554,25 euros soit moins de 48 centimes d'euros pour une augmentation de revenu de 2 euros. Il n'y a donc pas de saut, la fonction I est continue. On peut vérifier cette propriété pour le passage de chaque tranche. C'est l'objectif de la constante soustractive ajoutée dans chaque fonction affine. L'impression subjective de discontinuité provient du fait que le taux change brusquement : la pente de la droite change brusquement créant un point anguleux. On dit que la fonction n'est pas dérivable.

Une deuxième idée couramment répandue est que le saut de tranche peut entraîner une perte de revenu réel. Si le revenu réel correspond au revenu après déduction auquel on ôte les impôts, on a R' = R - I et R' reste en fait une fonction continue de R. C'est de nouveau une fonction affine par morceaux dont l'expression est :

• Si R < 4412 alors R' = R
• Si R ${\displaystyle \in }$ [4412 ; 8677] alors R' = R × 0,9317 + 301,84
• Si R ${\displaystyle \in }$ ]8677 ; 15274] alors R' = R × 0,8086 + 1369,48
• Si R ${\displaystyle \in }$ ]15274 ; 24731] alors R' = R × 0,7174 + 2762,47
• Si R ${\displaystyle \in }$ ]24731 ; 40241] alors R' = R × 0,6262 + 5017,93
• Si R ${\displaystyle \in }$ ]40241 ; 49624] alors R' = R × 0,5738 + 7126,56
• Si R > 49624 alors R' = R × 0,5191 + 9841

Les pentes de tous les segments de droites ou demi-droites sont positives et la fonction R' est continue donc elle est aussi une fonction croissante : plus on gagne d'argent, plus il en reste après impôts.

La courbe représentative d'une fonction (en bleu) et d'une approximation affine par morceaux de celle-ci (en rouge).

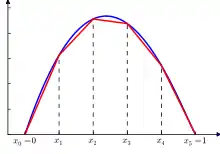
Une méthode courante utilisée pour les calculs numériques de fonctions (continues ou non) est de s'en donner une approximation affine par morceaux. C'est ce qui est à la base des calculs par la méthode des éléments finis d'ordre 1, et de la méthode de calcul intégral par la méthode des trapèzes.

Pour approcher une fonction f sur un intervalle [a , b] par une fonction affine par morceaux, on prend plusieurs points de l'intervalle a = x₀ < x₁ < ... < x_n = b, et de poser :

${\displaystyle \forall i\in [0;n],\ \forall x\in [x_{i},x_{i+1}],\ {\tilde {f}}(x)={\frac {f(x_{i+1})-f(x_{i})}{x_{i+1}-x_{i}}}x+{\frac {f(x_{i})+f(x_{i+1})}{2}}.}$

• Application linéaire par morceaux
• Fonction affine
• Régularité par morceaux