B-spline
En mathématiques, une B-spline est une combinaison linéaire de splines positives à support compact minimal. Les B-splines sont la généralisation des courbes de Bézier, elles peuvent être à leur tour généralisées par les NURBS.
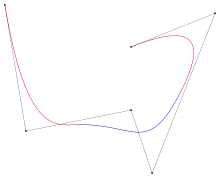
Définition
Étant donné m+1 nœuds ti dans [0, 1] avec une courbe spline de degré est une courbe paramétrique composée de fonctions B-splines de degré n , où les Pi forment un polygone appelé polygone de contrôle ; le nombre de points de contrôle composant ce polygone est égal à m-n.
Les m-n fonctions B-splines de degré n sont définies par récurrence sur le degré inférieur :
Quand les nœuds sont équidistants, c’est-à-dire quand ils sont en progression arithmétique, les B-splines sont dites « uniformes » : c'est le cas des courbes de Bézier qui sont des B-splines uniformes, dont les nœuds ti (pour i entre 0 et m) forment une suite arithmétique de 0 à 1 avec un pas constant 1/m, et où le degré n de la courbe de Bézier ne peut être supérieur à m.
Par extension, lorsque deux nœuds successifs et sont confondus, on pose : cela a pour effet de définir une discontinuité de la tangente, pour le point de la courbe paramétré par une valeur de t, donc d'y créer un sommet d'angle non plat ; toutefois il est souvent plus simple de définir ce « B-spline étendu » comme l'union de deux B-splines définis avec des nœuds distincts, ces splines étant simplement joints par ce sommet commun, sans introduire de difficulté dans l'évaluation paramétrique ci-dessus des B-splines pour certaines valeurs du paramètre t. Mais cela permet de considérer alors tout polygone simple comme un B-spline étendu.
Propriétés
La forme des fonctions de base est déterminée par la position des nœuds.
La courbe est à l'intérieur de l'enveloppe convexe des points de contrôle.
Une B-spline de degré n est non nulle dans l'intervalle [ti, ti+n+1[ :
En d'autres termes, déplacer un point de contrôle ne modifie que localement l'allure de la courbe.
B-splines en une dimension
Les B-splines peuvent être utilisées comme fonctions de base dans la théorie de l'approximation. La B-spline de degré n est donnée par : , où (y)+ est une version étendue de la fonction partie positive :
On reconnaît notamment la spline de degré 0 comme la fonction porte.
Ces fonctions ne sont pas interpolantes, mais leur régularité élevée sur un support compact en font des candidats intéressants dans l'approximation de fonctions[1].
Références
- (en) P. Thevenaz, T. Blu et M. Unser, « Interpolation revisited », IEEE Transactions on Medical Imaging, vol. 19, no 7, (DOI 10.1109/42.875199)
Liens internes
Liens externes
- (en) Splines: A unifying framework for image processing (tutoriel sur les B-splines)


![{\mathbf {S}}\,:\,[0,1]\to {\mathbb {R}}^{d}](https://img.franco.wiki/i/0810200773e532c15c6ac4cf44fcc1fc12667f96.svg)
![{\displaystyle \mathbf {S} (t)=\sum _{i=0}^{m-n-1}b_{i,n}(t).\mathbf {P} _{i}\,,\,t\in [t_{n},t_{m-n}]}](https://img.franco.wiki/i/7d235b4b53e760f4a272914221d18bff18d0f147.svg)








