Théorème de Cover

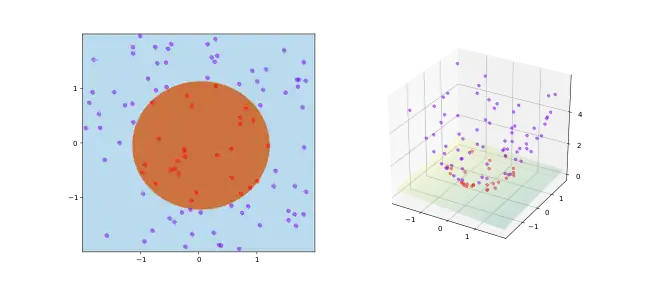
Le théorème de Cover est un énoncé de la théorie de l'apprentissage automatique et est l'une des principales motivations théoriques pour l'utilisation de l'astuce du noyau non linéaires dans les applications de l'apprentissage automatique. Le théorème stipule que, étant donné un ensemble de données d'apprentissage qui ne sont pas séparables par un classifieur linéaire, on peut avec une forte probabilité le transformer en un ensemble qui est linéairement séparable en le projetant dans un espace de dimension supérieure au moyen d'une transformation non linéaire. Le théorème est nommé d'après le théoricien de l'information Thomas M. Cover qui l'a énoncé en 1965. Dans sa propre formulation, il s’énonce comme suit :

« A complex pattern-classification problem, cast in a high-dimensional space nonlinearly, is more likely to be linearly separable than in a low-dimensional space, provided that the space is not densely populated.[1] »

L'image de gauche montre 100 échantillons dans l'espace réel de dimension 2. Ces échantillons ne sont pas séparables linéairement, mais en transposant les échantillons dans l'espace tridimensionnel avec l' astuce du noyau, les échantillons deviennent linéairement séparables. On observe que dans ce cas et dans de nombreux autres cas, il n'est pas nécessaire de placer les échantillons dans un espace de 99 dimensions comme dans la démonstration du théorème.

Démonstration

Étant donné $n$ échantillons, on les associe aux sommets d'un simplexe dans l'espace réel de dimension $n-1$ . Comme chaque partition des échantillons en deux ensembles est séparable par un séparateur linéaire, le théorème s'ensuit.

Notes et références

« Un problème de classification de modèles complexe, transposé de manière non linéaire dans un espace de grande dimension, est plus susceptible d'être linéairement séparable que dans un espace de dimension faible, à condition que l'espace ne soit pas densément peuplé ».

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Cover's theorem » (voir la liste des auteurs).

Simon Haykin, Neural Networks and Learning Machines, Upper Saddle River, New Jersey, Pearson Education Inc, 2009 (ISBN 978-0-13-147139-9), p. 232–236
Thomas.M. Cover, « Geometrical and Statistical properties of systems of linear inequalities with applications in pattern recognition », IEEE Transactions on Electronic Computers, vol. EC-14, n^o 3,‎ 1965, p. 326–334 (DOI 10.1109/pgec.1965.264137, lire en ligne)
Kishan Mehrotra, Chilukuri K. Mohan et S. Sanjay, Elements of artificial neural networks, MIT Press, 1997, 2^e éd. (ISBN 0-262-13328-8, lire en ligne) (Section 3.5)

Théorème de Cover

Démonstration

Notes et références

Article lié