Arbre cartésien

Introduits par Jean Vuillemin (1980)[2] dans le cadre des structures de données de recherche par plage géométrique, les arbres cartésiens ont également été utilisés dans la définition des arbres-tas et des structures de données d'arbres de recherche binaire randomisés pour les problèmes de recherche dichotomique. L'arbre cartésien pour une séquence peut être construit en temps linéaire en utilisant un algorithme basé sur la structure de pile pour trouver toutes les valeurs plus petites les plus proches dans une séquence.

L'arbre cartésien associé à une séquence de nombres distincts est un arbre binaire défini de manière unique par les propriétés suivantes :

1. L'arbre cartésien d'une séquence a un nœud pour chaque élément de la séquence, et chaque nœud est associé à un seul élément.
2. Un parcours symétrique de l'arbre (c'est-à-dire un parcours qui renvoie pour tout nœud, d'abord le résultat du parcours de son fils gauche, puis le nœud lui-même, puis le parcours de son fils droit) de l'arbre donne la séquence d'origine. En d'autres termes, le sous-arbre gauche se compose des valeurs antérieures à la racine dans l'ordre de séquence, tandis que le sous-arbre droit se compose des valeurs postérieures à la racine, et une contrainte de classement similaire s'applique à chaque nœud inférieur de l'arborescence.
3. L'arbre est un tas binaire : le parent éventuel de tout nœud a une valeur plus petite que le nœud lui-même[3].

En accord avec la définition d'un tas, la racine de l'arbre doit être le plus petit nombre de la séquence. Partant de là, on obtient une autre définition, récursive de l'arbre comme suit : la racine est la valeur minimale de la séquence, et les sous-arbres gauche et droit sont les arbres cartésiens pour les sous-séquences à gauche et à droite de la valeur racine. Cette définition donne une autre manière de construire l'arbre à partir de la séquence.

Si une séquence de nombres contient des répétitions, on peut toujours définir un arbre cartésien associé, mais il faut une règle supplémentaire pour comparer les éléments de valeur égale (on peut par exemple choisir que le premier de deux éléments égaux est traité comme le plus petit des deux) avant d'appliquer les règles ci-dessus.

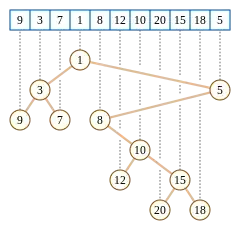
Un exemple d'arbre cartésien est illustré dans la figure en introduction.

Recherche de distance bidimensionnelle à l'aide d'un arbre cartésien: le point inférieur (rouge sur la figure) dans la région marquée qui à trois côtés : deux côtés verticaux et un côté horizontal (si la région n'est pas vide) peut être trouvé comme l'ancêtre commun le plus proche des points les plus à gauche et à droite (les points bleus sur la figure) à l'intérieur du carré défini par les limites verticales. Les points restants dans la région à trois côtés peuvent être trouvés en coupant l'arbre par une ligne verticale passant par le point inférieur et en se reproduisant.

Les arbres cartésiens peuvent être utilisés comme structure de données efficace pour la recherche d'un élément minimal dans un sous-tableau. Dans un arbre cartésien, cette valeur minimale est exactement celle du plus petit ancêtre commun des éléments les plus à gauche et à droite dans la sous-séquence que l'on cherche (cela se déduit des propriétés de l'arbre). Par exemple, dans la sous-séquence (12, 10, 20, 15) de la séquence montrée dans la première illustration, la valeur minimale de la sous-séquence (10) est le plus petit ancêtre commun des valeurs extrêmes de la séquence (12 et 15) dans l'arbre cartésien. Étant donné que le plus petit ancêtre commun peut être trouvé en temps constant, en utilisant une structure de données qui prend un espace linéaire à stocker et qui peut être construite en temps linéaire, les mêmes complexités temporelles et spatiales s'appliquent au problème de recherche d'un élément minimal de la sous-séquence.

Bender et Farach Colton (2000)[4] ont considéré cette relation dans l'autre sens afin de résoudre le problème de recherche d'un plus petit ancêtre commun en passant par un autre algorithme de recherche de minimum d'une sous-séquence. Leur structure de données utilise une technique basée sur des parcours eulériens pour transformer l'arbre d'entrée en une séquence, puis trouve des minima de plage dans la séquence résultante. La séquence résultant de cette transformation a une propriété intéressante (les nombres adjacents dans la séquence représentent les hauteurs des nœuds adjacents dans l'arbre et diffèrent donc de 1) dont ils profitent dans leur structure de données; pour résoudre le problème de minimisation de la sous-séquence pour les séquences qui n'ont pas cette propriété, ils passent par des arbres cartésiens pour transformer le problème de minimisation en un problème de plus petit ancêtre commun, puis appliquent leur algorithme pour avoir un problème sur une séquence qui a cette bonne propriété.

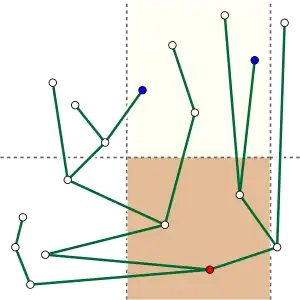
Le même problème de minimisation peut également être vu différemment, comme recherche de points dans un plan. En effet, un ensemble fini de points dans le plan cartésien peut être transformé en arbre cartésien : pour ce faire, on ordonne les points par leurs abscisses (pour avoir un unique ordre pour la séquence) et on considère leurs ordonnées comme leurs valeurs dans la séquence. On construit ensuite l'arbre cartésien associé. Si S est le sous-ensemble des points d'entrée dans un domaine délimité uniquement par ses abscisses : L ≤ X ≤ R, et si on note p le point le plus à gauche de S (donc d'abscisse minimale) et q le point le plus à droite de S (donc d'abscisse maximale), alors le plus petit ancêtre commun de p et q dans l'arbre cartésien est le point le plus bas de la dalle. On peut également chercher à répertorier tous les points dans une région délimitée par les inégalités L ≤ X ≤ R (abscisse) et y ≤ T (ordonnée), en trouvant ce point le plus bas b, puis en comparant son ordonnée à T, et (si le point se trouve dans la région à trois côtés) en continuant récursivement dans le sous-domaine au-dessus de b. De cette manière, une fois que les points les plus à gauche et à droite de la dalle ont été identifiés, tous les points dans la région à trois côtés peuvent être trouvés en temps linéaire (en le nombre de points).

La recherche de plus petit ancêtre commun dans un arbre cartésien permet également de construire une structure de données en complexité spatiale linéaire qui permet de trouver les distances entre deux points d'un espace ultramétrique (s'il est fini) en temps constant. La distance à l'intérieur d'un ultramétrique est la même que le poids du trajet minimax dans l'arbre couvrant minimum de l'espace muni de la distance ultramétrique. À partir de l'arbre couvrant minimum, on peut construire un arbre cartésien, dont le nœud racine représente l'arête de poids maximal de l'arbre couvrant minimum. La suppression de cette arête partitionne l'arbre couvrant en deux sous-arbres, et on peut alors construire récursivement l'arbre cartésien en appliquant la même règle pour les deux sous-arbres, qui donneront les deux fils du premier nœud . Les feuilles de l'arbre cartésien représentent des points de l'espace métrique, et le plus petit ancêtre commun de deux feuilles de l'arbre cartésien est l'arête de poids maximal entre ces deux points dans l'arbre couvrant minimum, qui a un poids égal à la distance entre les deux points par définition de la distance ultramétrique. Une fois l'arbre couvrant minimum trouvé et les poids de ses arêtes triés, l'arbre cartésien peut être construit en temps linéaire (cependant, il n'est pas unique cette fois).

Étant donné qu'un arbre cartésien est un arbre binaire, il semble naturel de l'utiliser comme arbre binaire de recherche pour une séquence ordonnée de valeurs. Cependant, essayer de construire un arbre cartésien comme on construit un arbre binaire de recherche ne fonctionne pas bien : l'arbre cartésien d'une séquence triée est en fait un chemin, enraciné à son extrémité la plus à gauche, et la recherche binaire dans cet arbre est finalement équivalente à une recherche séquentielle naïve de la liste elle-même. Cependant, il est possible de générer des arbres de recherche plus équilibrés en imposant des valeurs de priorité pour chaque élément (différentes des valeurs présentes dans la séquence), qui vont servir à imposer l'ordre des sommets de l'arbre cartésien. Cette construction se rapproche de celle faite dans le cadre géométrique décrit au dessus, dans lequel les abscisses d'un ensemble de points sont les clés de recherche et les ordonnées sont les priorités.

Cette idée a été appliquée par Seidel et Aragon (1996)[5], qui ont suggéré l'utilisation de nombres aléatoires pour les priorités. La structure de données résultant de ce choix aléatoire est appelée « treap » (ou parfois « arbre-tas » en français), car il combine arbre binaire de recherche (tree en anglais) et propriété des tas (heap en anglais). On effectue généralement l'insertion dans un treap en ajoutant la nouvelle clé en tant que feuille d'un arbre existant, en choisissant une priorité aléatoire pour celle-ci pour celui-ci, puis en effectuant des opérations de rotation de l'arbre le long d'un chemin allant du nœud à la racine de l'arbre afin de bien avoir toutes les propriétés du tas; de même, pour supprimer un élément, on l'enlève et le remplace par un de ses fils, puis on effectue des rotations le long d'un seul chemin dans l'arbre.

Si les priorités de chaque clé sont choisies au hasard (et indépendamment) au moment où la clé est insérée dans l'arbre, l'arbre cartésien résultant aura les mêmes propriétés qu'un arbre de recherche binaire aléatoire, un arbre calculé en insérant les clés dans une permutation choisie au hasard en commençant à partir d'un arbre vide, chaque insertion laissant inchangée la structure d'arbre précédente et insérant le nouveau nœud comme une feuille de l'arbre. Les arbres de recherche binaires aléatoires ont été bien plus étudiés et sont connus pour avoir de bonnes propriétés en tant qu'arbres de recherche (ils ont une profondeur logarithmique avec une probabilité élevée); on retrouve cela dans les treaps. Il est également possible, comme le suggèrent Aragon et Seidel, de redéfinir les priorités des nœuds importants ou plus souvent recherchés afin de les rapprocher de la racine et donc faciliter leur accès (avec une meilleure complexité temporelle).

Un arbre cartésien peut être construit en temps linéaire à partir de sa séquence d'entrée. Une méthode consiste à traiter simplement les valeurs de la séquence de gauche à droite, de manière qu'à chaque étape, l'arbre partiellement construit soit cartésien. On utilise alors une structure qui permet à la fois de parcourir l'arbre vers le haut et vers le bas. Pour traiter une nouvelle valeur x, on considère le nœud représentant la valeur avant x dans la séquence et on suit le chemin entre ce nœud et la racine de l'arbre jusqu'à trouver une valeur y inférieure à x . Ce nœud y devient le parent de x, et le précédent fils droit de y devient le nouvel fils gauche de x . Le temps d'exécution de cette fonction est linéaire, car le temps de recherche du parent y de chaque nouveau nœud x est compensé par le nombre de nœuds qui sont supprimés du chemin le plus à droite de l'arbre.

Un autre algorithme de construction en temps linéaire est basé sur le problème des plus proches valeurs les plus petites . Dans la séquence d'entrée, on peut définir le voisin gauche d'une valeur x comme étant la valeur à gauche de x et plus petite que x la plus proche dans la séquence. Le voisin droit est défini de la même manière. La séquence des voisins gauches peut être trouvée par un algorithme utilisant une pile qui contiendra une sous-séquence de la séquence d'entrée. Pour chaque nouvelle valeur x, la pile est dépilée jusqu'à ce qu'elle soit vide ou que son premier élément soit plus petit que x, puis on empile x. Le voisin gauche de x est l'élément supérieur au moment où x est empilé, la pile est donc exactement la séquence des voisins gauches successifs. Les voisins droits peuvent être trouvés en appliquant le même algorithme de pile à la séquence renversée (ou en partant de l'autre côté de la pile). Le parent de x dans l'arbre cartésien est le plus grand entre le voisin gauche de x et le voisin droit de x, si au moins un existe (sinon x est la racine). Les voisins gauche et droit peuvent également être construits efficacement par des algorithmes parallèles. Cette formulation peut donc être utilisée pour développer des algorithmes parallèles efficaces pour la construction d'arbres cartésiens.

Un autre algorithme en temps linéaire pour la construction d'arbres cartésiens est basé sur une méthode "diviser pour régner". Ici, l'algorithme construit récursivement l'arbre sur chaque moitié de la séquence d'entrée, puis fusionne les deux arbres en réalisant une opération de fusion classique. L'algorithme est également parallélisable car à chaque niveau de récursivité, chacun des deux sous-problèmes peut être calculé en parallèle, et l'opération de fusion peut également être efficacement parallélisée[6].

Paires de valeurs consécutives de la séquence (représentées par les bords rouges épais) qui encadrent une valeur de séquence x (le point bleu foncé). Le coût d'inclusion de x dans l'ordre de tri produit par l'algorithme de Levcopoulos – Petersson est proportionnel au logarithme de ce nombre de paires de parenthèses.

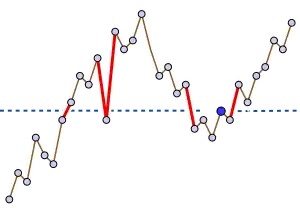
Levcopoulos et Petersson (1989)[7] ont décrit un algorithme de tri basé sur des arbres cartésiens. L'algorithme original utilise un arbre avec le maximum à la racine, mais il peut être facilement modifié pour prendre en entrée un arbre cartésien avec la valeur minimale à la racine. Par souci de cohérence, c'est donc cette version adaptée de l'algorithme qui est décrite ci-dessous.

L'algorithme de Levcopoulos-Petersson peut être considéré comme une version du tri par sélection ou du tri par tas qui utilise une file de priorité des valeurs minimales possibles et qui à chaque étape trouve et supprime la valeur minimale dans cette file d'attente, tout en l'ajoutant à la fin d'une séquence de sortie (la séquence triée). Dans cet algorithme, la file de priorité se compose uniquement d'éléments dont le parent dans l'arbre cartésien a déjà été trouvé et supprimé. Ainsi, l'algorithme comprend les étapes suivantes :

1. Construire un arbre cartésien pour la séquence d'entrée
2. Initialiser une file d'attente prioritaire, contenant initialement uniquement la racine de l'arborescence
3. Alors que la file d'attente prioritaire n'est pas vide :
   • Rechercher et supprimer la valeur minimale x dans la file d'attente prioritaire
   • Ajouter x à la séquence de sortie
   • Ajouter les fils du noeud x à la file de priorité

Comme le montrent Levcopoulos et Petersson, la taille de la file d'attente prioritaire restera petite pour les séquences d'entrée qui sont déjà presque triées. Cette méthode à donc l'avantage d'être rapide lorsqu'il n'y a plus beaucoup d'échanges à faire. Plus précisément, le temps d'exécution le plus défavorable de cet algorithme est O ( n log k ), où k est la moyenne, sur toutes les valeurs x de la séquence, du nombre de paires de valeurs consécutives de la séquence qui encadrent x . Ils montrent également l'existence d'une borne inférieure de complexité : pour tout n et k = ω (1), tout algorithme de tri par comparaison doit utiliser Ω ( n log k ) comparaisons dans les pires cas.

Les arbres cartésiens ont été introduits et nommés par Jean Vuillemin (1980). Le nom est dérivé du système de coordonnées cartésiennes utilisé pour repérer des points du plan : Vuillemin les a initialement définis comme dans la partie sur la recherche bidimensionnelle de points, avec donc un arbre cartésien pour un ensemble de points du plan, triés par abscisses ayant la propriété des tas pour les ordonnées des points. Gabow, Bentley, Tarjan (1984)[8] et les auteurs suivants ont ensuite choisi la définition d'un arbre cartésien à partir d'une séquence; c'est en fait une généralisation de la définition donnée par Vuillemin pour permettre ses applications à des séquences quelconques et des problèmes non géométriques. Dans certaines références, l'ordre est renversé, ce qui signifie que le parent d'un nœud a toujours une valeur plus grande que ce nœud.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Cartesian tree » (voir la liste des auteurs).

• Michael A. Bender et Martin Farach-Colton, « The LCA problem revisited », Proceedings of the 4th Latin American Symposium on Theoretical Informatics, Springer-Verlag, Lecture Notes in Computer Science (1776),‎ 2000, p. 88–94 (lire en ligne).
• Omer Berkman, Baruch Schieber et Uzi Vishkin, « Optimal doubly logarithmic parallel algorithms based on finding all nearest smaller values », Journal of Algorithms, vol. 14, n^o 3,‎ 1993, p. 344–370 (DOI 10.1006/jagm.1993.101).
• Maxime Crochemore et Luís M.S. Russo, « Cartesian and Lyndon trees », Theoretical Computer Science, vol. 806,‎ 2020, p. 1–9 (DOI 10.1016/j.tcs.2018.08.011)
• Erik D. Demaine, Gad M. Landau et Oren Weimann, « On Cartesian trees and range minimum queries », Automata, Languages and Programming, 36th International Colloquium, ICALP 2009, Rhodes, Greece, July 5-12, 2009, Springer-Verlag, Lecture Notes in Computer Science (5555),‎ 2009, p. 341–353 (ISBN 978-3-642-02926-4, DOI 10.1007/978-3-642-02927-1_29).
• Johannes Fischer et Volker Heun, « Theoretical and Practical Improvements on the RMQ-Problem, with Applications to LCA and LCE », Springer-Verlag Lecture Notes in Computer Science (4009),‎ 2006, p. 36–48 (ISBN 978-3-540-35455-0, DOI 10.1007/11780441_5)
• Johannes Fischer et Volker Heun, « A New Succinct Representation of RMQ-Information and Improvements in the Enhanced Suffix Array », Springer-Verlag, Lecture Notes in Computer Science (4614),‎ 2007, p. 459–470 (ISBN 978-3-540-74449-8, DOI 10.1007/978-3-540-74450-4_41)
• Harold N. Gabow, Jon Louis Bentley et Robert E. Tarjan, « Scaling and related techniques for geometry problems », STOC '84: Proc. 16th ACM Symp. Theory of Computing, New York, NY, USA, ACM,‎ 1984, p. 135–143 (ISBN 0-89791-133-4, DOI 10.1145/800057.808675).
• Dov Harel et Robert E. Tarjan, « Fast algorithms for finding nearest common ancestors », SIAM Journal on Computing, vol. 13, n^o 2,‎ 1984, p. 338–355 (DOI 10.1137/0213024).
• T. C. Hu, « The maximum capacity route problem », Operations Research, vol. 9, n^o 6,‎ 1961, p. 898–900 (DOI 10.1287/opre.9.6.898, JSTOR 167055).
• Bruno Leclerc, « Description combinatoire des ultramétriques », Centre de Mathématique Sociale. École Pratique des Hautes Études. Mathématiques et Sciences Humaines, n^o 73,‎ 1981, p. 5–37, 127 (MR 623034).
• Christos Levcopoulos et Ola Petersson, « Heapsort - Adapted for Presorted Files », WADS '89: Proceedings of the Workshop on Algorithms and Data Structures, Springer-Verlag, Lecture Notes in Computer Science (382),‎ 1989, p. 499–509 (DOI 10.1007/3-540-51542-9_41).
• Raimund Seidel et Cecilia R. Aragon, « Randomized Search Trees », Algorithmica, vol. 16, n^os 4/5,‎ 1996, p. 464–497 (DOI 10.1007/s004539900061, lire en ligne).
• Baruch Schieber et Uzi Vishkin, « On finding lowest common ancestors: simplification and parallelization », SIAM Journal on Computing, vol. 17, n^o 6,‎ 1988, p. 1253–1262 (DOI 10.1137/0217079).
• Julian Shun et Guy E. Blelloch, « A Simple Parallel Cartesian Tree Algorithm and its Application to Parallel Suffix Tree Construction », ACM Transactions on Parallel Computing, vol. 1,‎ 2014, p. 1–20 (DOI 10.1145/2661653).
• Jean Vuillemin, « A unifying look at data structures », Communications of the ACM, New York, NY, USA, ACM, vol. 23, n^o 4,‎ 1980, p. 229–239 (DOI 10.1145/358841.358852).