Treap

Un arbre binaire dont les clés sont alphabétiques et dont l'ordre de tas max est celui des nombres

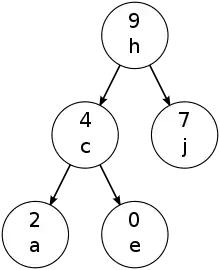
L'arbretas a été décrit pour la première fois par Cecilia R. Aragon et Raimund Seidel en 1989[1] - [2]; son nom est un mot-valise issu de l'arbre et du tas. Il s'agit d'un arbre binaire généré à partir d'un ensemble de nombres[3] dans lequel chaque clé se voit assignée une priorité numérique choisie aléatoirement. Tout comme pour n'importe quel arbre binaire de recherche, l'ordre infixe sur les nœuds est le même que celui des clés ordonnés. La structure d'un arbre est déterminée par la restriction qu'il possède la propriété de tas: c'est-à-dire que, la priorité pour tout nœud interne doit être plus grande que la priorité de ses enfants. Ainsi, le nœud racine doit être le nœud de plus grande priorité, et ses sous-arbres gauches et droits sont formés de la même manière à partir des éléments respectivement plus petits et plus grand que l'élément stocké dans la racine.

Une manière équivalente de définir un arbretas et de dire qu'il est formé en insérant les nœuds selon leur ordre de priorité, de la plus grande à la plus petite dans un arbre binaire de recherche, sans faire aucun rééquilibrage. Ainsi, si les priorités sont des nombres aléatoires indépendants (avec une distribution sur un espace assez large pour qu'il y ait assez de place pour toutes les priorités de sorte que deux nœuds aient très peu de chance d'avoir la même priorité) alors la forme de l'arbretas a la même distribution de probabilité que la forme d'un arbre binaire de recherche randomisé, un arbre de recherche formé en insérant les nœuds sans rééquilibrage avec un ordre d'insertion choisi aléatoirement. Parce que les arbres binaires de recherche randomisés sont connus pour avoir avec une forte probabilité une hauteur logarithmique, la même chose est vraie pour les arbretas.

Aragon et Seidel ont aussi suggéré d'assigner les plus fortes priorités aux nœuds les plus fréquemment visités, par exemple par un processus qui, à chaque accès, choisit un nombre aléatoire et remplace la priorité du nœud par celle de ce nombre si elle est plus grande que la priorité précédente. Cette modification ferait perdre à l'arbre sa forme aléatoire, car les nœuds accédés fréquemment auraient plus de chance d'être proche de la racine de l'arbre, permettant à leur recherche d'être plus rapide.

Blelloch et Reid-Miller[4] décrivent une application des arbretas au problème de maintenir des ensembles de nombres et d'effectuer des opérations d'unions, d'intersections, et de différences, en utilisant un arbretas pour décrire ces ensembles. Naor et Nissim[5] en décrivent une autre application dont le but est de maintenir des certificats de clés publiques dans un système de cryptographie à clé publique.

En particulier, les arbretas supportent les opérations suivantes :

• Rechercher une clé donnée avec l'algorithme standard de recherche dichotomique dans un arbre binaire de recherche, en ignorant les priorités.
• Insérer une nouvelle clé x dans l'arbretas : il faut générer une priorité aléatoire y pour x, puis faire une recherche dichotomique de x dans l'arbre, et créer un nouveau nœud à la place de la feuille où l'algorithme de recherche s'arrête. Ensuite, tant que x n'est pas la racine de l'arbre et possède une priorité supérieure à celle de son parent z, on effectue une rotation qui échange la relation parent-enfant entre x et z.
• Pour supprimer un nœud x de l'arbretas, si x est une feuille de l'arbre, on se contente de le supprimer. Si x a un seul enfant z, on supprime x de l'arbre et on fait de z l'enfant du parent de x (ou la racine de l'arbre si x n'avait pas de parent). Finalement, si x a deux enfants, on échange sa position dans l'arbre avec la position de son successeur immédiat z selon l'ordre croissant. Dans ce cas final, l'échange pourrait briser la propriété de tas pour z, donc des rotations supplémentaires doivent être effectuées pour restaurer cette propriété.
• Pour séparer un arbretas en deux arbretas plus petits, celui dont les clés sont plus petites qu'une clé x et celui dont les clés sont plus grandes que x, on insère x dans l'arbretas avec une priorité supérieure aux autres priorités de l'arbretas. Après l'insertion, x sera ainsi la racine de l'arbretas, toutes les valeurs plus petites que x se trouveront dans le sous-arbre gauche, celles plus grandes dans le sous-arbre droit. Cette opération a le même qu'une simple insertion dans l'abretas.
• Pour fusionner deux arbretas issus d'une séparation, on peut sans risque supposer que la plus grande valeur dans le premier arbretas est plus petite que toutes les valeurs dans le second arbretas. On insère une nouvelle valeur x, telle que x soit comprise entre la plus grande valeur du premier arbretas et la plus petite valeur du second, et on attribue à x la plus petite priorité. Après l'insertion, x sera une feuille, et pourra ainsi facilement être supprimée. Le résultat est un arbretas qui est la fusion des deux arbretas originaux. Le coût est à nouveau le même qu'une insertion.

L'arbre binaire de recherche randomisé, introduit par Martínez et Roura à la suite du travail de Aragon et Seidel sur les arbretas[6], stocke les mêmes nœuds avec la même distribution aléatoire sur la forme de l'arbre, mais conserve des informations différentes dans les nœuds de l'arbre afin de maintenir sa structure randomisée.

Au lieu de stocker des priorités aléatoires pour chaque nœud, l'arbre binaire de recherche randomisé stocke un petit entier dans chaque nœud, qui est le nombre de ses descendants (lui-même étant un de ses descendants); ces valeurs peuvent être mises à jour pour chaque rotation en un temps constant. Quand une clé x est insérée dans un arbre qui a déjà n nœuds, l'algorithme d'insertion choisit avec une probabilité de 1/(n + 1) de placer x comme la nouvelle racine de l'arbre, et sinon il appelle récursivement la procédure d'insertion pour insérer x dans le sous-arbre gauche ou le sous-arbre droit (en fonction du fait que sa clé soit plus grande ou plus petite que celle de la racine). Le nombre de descendants est utilisé par l'algorithme pour calculer les probabilités nécessaires aux choix aléatoires effectués à chaque étape. Placer x à la racine du sous-arbre peut être effectué soit comme dans l'arbretas en l'insérant comme feuille et en le faisant remonter avec des rotations, soit par un algorithme alternatif décrit par Martínez et Roura qui divise le sous-arbre en deux morceaux qui peuvent être utilisés comme les fils gauches et droits du nouveau nœud.

La procédure de suppression pour un arbre binaire de recherche randomisé utilise pour chaque nœud les mêmes informations que la procédure d'insertion, et de même que la procédure d'insertion, elle fait une suite de O(log n) décisions aléatoires afin de réunir les deux sous-arbres gauches et droits du nœud supprimé. Si le sous-arbre gauche ou droit du nœud supprimé est vide, l'opération de réunion est triviale; sinon, le fils gauche ou le fils droit du nœud supprimé est choisi comme nouvelle racine du sous-arbre avec une probabilité proportionnelle à son nombre de descendants, et la réunion se fait récursivement.

L'information stockée par les nœuds dans l'arbre binaire randomisée est plus simple que celle stockée dans les arbres tas (un petit entier au lieu d'un nombre aléatoire flottant), mais il demande un plus grand nombre d'appels au générateur de nombres aléatoires (O(log n) appels par insertion ou suppression au lieu d'un seul appel par insertion) et la procédure d'insertion est légèrement plus compliquée du fait de la nécessité de mettre à jour le nombre de descendants. Un différence technique mineure est que, dans un arbretas, il y a une probabilité plus petite de collision (deux clés recevant la même priorité), et dans les deux cas il y aura une différence statistique entre un véritable générateur de nombre aléatoire et le générateur de nombres pseudo-aléatoires utilisé en général sur ordinateurs. Néanmoins, dans tous les cas la différence entre le modèle théorique du choix parfaitement aléatoire employé dans la conception de l'algorithme et les capacités d'un générateur de nombres aléatoires sont négligeables.

Bien que l'arbretas et l'arbre binaire de recherche randomisé aient tous les deux la même distribution aléatoire sur la forme de leurs arbres après chaque mise à jour, l'historique des modifications effectuées sur les arbres effectuées par ces deux structures de données sur une suite d'insertions et de suppressions, peuvent être différentes. Par exemple, dans un arbretas, si les trois nombres 1, 2 et 3 sont insérés dans l'ordre 1, 3, 2, et ensuite le nombre 2 est supprimé, les deux structures d'arbre ne donnent pas nécessairement le même résultat en fonction des choix randomisés.

• Collection of treap references and info par Cecilia Aragon
• Open Data Structures - Section 7.2 - Treap: A Randomized Binary Search Tree

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Treap » (voir la liste des auteurs).