Arbre de recherche
En informatique, un arbre de recherche est un arbre enraciné utilisé pour localiser des clés spécifiques à partir d'un ensemble. Afin qu'un arbre fonctionne comme un arbre de recherche, l'étiquette (la valeur contenue dans le nœud) de chaque nœud doit être supérieure à toutes les étiquettes dans le sous-arbre gauche et inférieure à toutes les étiquettes dans le sous-arbre droit[1].
L'avantage des arbres de recherche est leur temps de recherche efficace à condition que l'arbre soit raisonnablement équilibré, c'est-à-dire que les feuilles soient à des profondeurs comparables. Différentes structures de données d'arbre de recherche existent, dont plusieurs permettent également une insertion et une suppression efficace des éléments, tout en maintenant l'équilibre de l'arbre.
Les arbres de recherches sont souvent utilisés pour implémenter un tableau associatif.
Type d'arbres
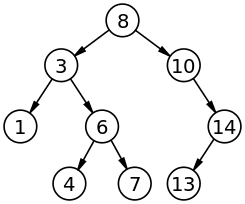
Arbre binaire de recherche
Un arbre binaire de recherche est une structure de données basée sur des nœuds où chaque nœud contient une étiquette et deux sous-arbres, le gauche et le droit. Pour chaque nœud, l'étiquette de la sous-arborescence gauche doit être inférieure à l'étiquette du nœud actuel, et l'étiquette du sous-arbre droit doit être supérieure à l'étiquette du nœud. Ces sous-arbres doivent aussi être des arbres binaires de recherche.
La complexité en temps pour chercher un élément requiert un temps en O(log(n)) dans le cas moyen, mais O(n) dans le cas critique où l'arbre est complètement déséquilibré et ressemble à une liste chaînée.
Arbre B
Un arbre B est une généralisation des arbres binaires de recherche dans le sens où il peut avoir un nombre variable de sous-arbres à chaque nœud. Ce principe minimise la taille de l'arbre et réduit le nombre d'opérations d'équilibrage. De plus un B-arbre grandit à partir de la racine, contrairement à un arbre binaire de recherche qui croît à partir des feuilles.
Le créateur des arbres B, Rudolf Bayer, n'a pas explicité la signification du « B ». L'explication la plus fréquente est que le B correspond au terme anglais « balanced » (en français : « équilibré »). Cependant, il pourrait aussi découler de « Bayer », du nom du créateur, ou de « Boeing », du nom de la firme pour laquelle le créateur travaillait (Boeing Scientific Research Labs).
En raison de leur nombre de nœuds variable, les arbres B sont optimisés pour les systèmes qui lisent de gros blocs de données. Ils sont également couramment utilisés dans les bases de données.
La complexité en temps pour chercher un élément requiert un temps en O(log(n)).
(a,b)-arbre
Un (a,b)-arbre est un arbre de recherche où toutes les feuilles sont à la même profondeur. Chaque nœud a au moins a fils et au plus b' fils, et la racine a au moins 2 fils et au plus b fils.
a et b peuvent être décidés avec la formule suivante[2] :
La complexité en temps pour chercher un élément requiert un temps en O(log(n)).
Arbre ternaire de recherche
Un arbre ternaire de recherche (ATR ou TST — pour Ternary Search Tree en anglais) est une structure de données adaptée pour la recherche et combinant les avantages d'un arbre binaire de recherche et d'un arbre préfixe.
La complexité en temps pour chercher un élément dans un arbre ternaire de recherche équilibré requiert un temps en O(log(n)).
Algorithmes de recherche
Recherche d'une étiquette spécifique
En supposant que l'arbre est ordonné, on peut prendre une étiquette et essayer de la localiser dans l'arbre. Les algorithmes suivants sont pour un arbre binaire de recherche, mais la même idée peut être appliquée pour des arbres plus généraux.
Récursivement
recherche-récursive(étiquette, nœud)
si nœud est NULL
retourner ARBRE_VIDE
si étiquette < nœud.étiquette
retourner recherche-récursive(étiquette, nœud.gauche)
sinon si étiquette > nœud.étiquette
retourner recherche-récursive(étiquette, nœud.droite)
sinon
retourner nœud
Itérativement
recherche-itérative(étiquette, nœud)
nœudCourant := nœud
tant que nœudCourant n'est pas NULL
si nœudCourant.étiquette = étiquette
retourner nœudCourant
sinon si nœudCourant.étiquette > étiquette
nœudCourant := nœudCourant.gauche
sinon
nœudCourant := nœudCourant.droite
Recherche du Min et du Max
Dans un arbre trié, le minimum est situé dans le nœud le plus profondément à gauche, et le maximum est situé dans le nœud le plus profond à droite[3].
Minimum
trouverMinimum(nœud)
si nœud est NULL
retourner ARBRE_VIDE
min := nœud
tant que min.gauche n'est pas NULL
min := min.gauche
retourner min.étiquette
Maximum
trouverMaximum(nœud)
si nœud est NULL
retourner ARBRE_VIDE
max := nœud
tant que max.droite n'est pas NULL
max := max.droite
retourner max.étiquette
Références
- Black, Paul and Pieterse, Vreda (2005). "search tree". Dictionary of Algorithms and Data Structures
- Toal, Ray. "(a,b) Trees"
- Gildea, Dan (2004). "Binary Search Tree"
