Tas (informatique)
En informatique, un tas[1] (ou monceau au Canada[2], heap en anglais) est une structure de données de type arbre qui permet de retrouver directement l'élément que l'on veut traiter en priorité. C'est un arbre binaire presque complet ordonné. Un arbre binaire est dit presque complet si tous ses niveaux sont remplis, sauf éventuellement le dernier, qui doit être rempli sur la gauche (cf. Contre-exemples). Ses feuilles sont donc à la même distance minimale de la racine, plus ou moins 1.
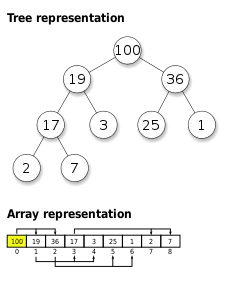
Pour utiliser un tas, les clés sont ordonnées selon la propriété de tas : la clé d'un nœud parent a une plus haute priorité que les clés de ses enfants. La "priorité" signifie ici que les clés des enfants sont, soit toutes inférieures, soit toutes supérieures, suivant que le tas est ordonné pour avoir en racine la clé maximale (max heap) ou minimale (min heap). Une fois traitée, la donnée de plus haute priorité peut ou non être enlevée, ce qui modifie le tas.
Les tas ont été introduits par J. W. J. Williams (en) en 1964 pour l'algorithme du tri par tas (cf la section ci-après pour une première introduction à ce tri)[3].
Description
On dit qu'un arbre est ordonné en tas lorsque la propriété suivante est vérifiée :
Pour tous nœuds A et B de l'arbre tels que B soit un fils de A
clé(A) ≥ clé(B)
ou
Pour tous nœuds A et B de l'arbre tels que B soit un fils de A
clé(A) ≤ clé(B)
Un arbre vérifiant cette propriété est aussi appelé « arbre tournoi »[4]. Cette propriété implique que la plus grande clé (ou la plus petite) soit située à la racine du tas. Ils sont ainsi très utilisés pour implémenter les files à priorités car ils permettent des insertions en temps logarithmique et un accès direct au plus grand élément. L'efficacité des opérations effectuée sur des tas est très importante dans de nombreux algorithmes sur les graphes. Les tas sont en outre utilisés dans l'algorithme de tri par tas.
On peut ainsi représenter un tas à n éléments par un tableau à n cases, de la façon suivante :
Si on note 0 le numéro de la racine du tas, on peut définir récursivement le numéro de tous les sommets dans l'arbre, grâce à la formule : pour un sommet parent numéroté i, son fils gauche aura pour numéro 2i+1, et son fils droit 2i+2. Le parent d'un sommet j a donc toujours pour numéro la partie entière inférieure de (j-1)/2.
Remarques
- La notion de plus grande clé est équivalente à la notion de plus petite clé, seule diffère la relation d'ordre total utilisée. Les algorithmes restent donc les mêmes si l'on veut accéder directement au plus petit élément et non au plus grand. On peut même, dans la plupart des langages de programmation modernes, programmer de façon à passer la relation d'ordre désirée en paramètre des algorithmes de construction et de manipulation de tas.
Attention : un tas est organisé selon une seule relation d'ordre à la fois. Il faut donc décider dès sa construction si l'on veut accéder ensuite au plus grand élément, ou au plus petit, et selon quel attribut de l'objet stocké dans l'étiquette de chaque nœud. Les manipulations suivantes de ce tas devront obligatoirement se faire par rapport à la même relation d'ordre.
Contre-exemples
Les deux contre-exemples suivants ont pour relation d'ordre :
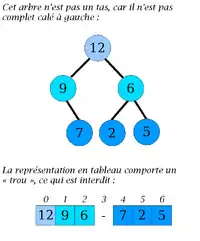 Contre-exemple no 1 |
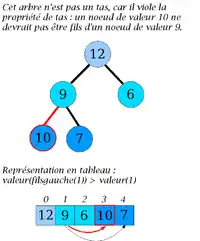 Contre-exemple no 2 |
Primitives
Outre les primitives générales existant sur toute structure de données (taille, création de structure vide, etc.), on définit sur un tas les opérations élémentaires suivantes ; les complexités sont données dans le pire des cas, sans tenir compte de l’amortissement survenant dans les situations réelles. Dans toute la suite, on considère qu'un tas est implémenté comme un tableau, comme expliqué dans la définition, et on considère que c'est la plus grande clé qui est à la racine. (les implémentations sont en Pseudo-code puis Python, on note T le tas, i représente un indice et e un élément) :
Enfiler
Pour enfiler un élément, on le place comme feuille, puis on fait "remonter" l'élément pour maintenir la priorité du tas.
Pseudo-code :
Fonction enfiler (T,e) ajouter e à T en dernière position T.taille=T.taille+1 appeler tasser_1 (T,T.taille) retourner T
Python :
def enfiler(T, e):
"""On ajoute une feuille au tas, et on la tasse"""
T = T + [e]
tasser_1(T, len(T) - 1)
return T
La fonction tasser_1 prend en entrée un arbre binaire presque complet, tel que celui-ci est un tas, sauf éventuellement au niveau de T[i], et retourne l'arbre réordonné en tas. Pour cela, il compare T[i] à son parent, on les échange si T[i] est plus grand que son parent, et on recommence, ou alors on stoppe l'algorithme :
Pseudo-code :
Fonction tasser_1 (T,i) k = si k = échanger et appeler tasser_1 (T,)
Python :
import numpy as np
def tasser_1(T, index):
"""On tasse des feuilles vers la racine"""
# a//b correspond au quotient de a par b
index_parent = (index - 1) // 2
# np.argmax permet de renvoyer la place du plus grand élément d'un tableau donné
# ex: np.argmax([3,1,2]) renvoie 0
k = np.argmax([T[index], T[index_parent]])
if k == 0:
# Echange des deux noeuds: a,b = b,a
T[index], T[index_parent] = T[index_parent], T[index]
# Si le noeud parent n'est pas la racine
# on continue de tasser à partir de l'index parent
if index_parent != 0:
tasser_1(T, index_parent)
L’opération peut être réalisée en O(log(n)). Dans certaines implémentations, l’insertion est en temps constant mais la propriété de tas n’est pas conservée.
Défiler
Quand on défile un élément d'un tas, c'est toujours celui de priorité maximale. Il correspond donc à la racine du tas. L’opération peut conserver la structure de tas avec une complexité de O(log(n)) ; en effet, il ne reste alors qu'à réordonner l'arbre privé de sa racine pour en faire un nouveau tas, en plaçant la dernière feuille à la racine, puis par tamisage successif (on peut également seulement lire l'élément, sans pour autant le supprimer du tas, en temps constant) :
Pseudo-code :
Fonction défiler (T) m:=T[1] T[1]:=T[T.taille] T.taille=T.taille-1 appeler tasser (T,1) retourner m
Python :
def defiler(T):
m = T[0]
T[0] = T[-1] # T[-1] correspond au derner élément de T
T = T[:-1] # T[:-1] correspond au tableau T sans le dernier élément
tasser(T, 0)
return m
La fonction tasser prend en entrée un arbre binaire presque complet, tel que T est un tas sauf éventuellement en T[i], et retourne l'arbre réordonné en un tas.
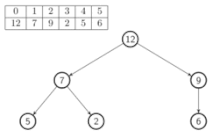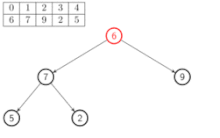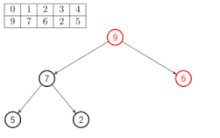
Pseudo-code :
Fonction tasser (T,i) k= si ki échanger et appeler tasser (T,k)
Python :
import numpy as np
def tasser(T, index):
"""On tasse de la racine vers les feuilles"""
index_fils_gauche = index * 2 + 1
index_fils_droit = index * 2 + 2
# Verification de la présence d'un fils droit
if index_fils_droit < len(T):
A = [T[index], T[index_fils_gauche], T[index_fils_droit]]
else:
A = [T[index], T[index_fils_gauche]]
# L'ordre de A permet d'obtenir un décalage (0, 1 ou 2)
decalage = np.argmax(A)
# Si le décalage vaut 0, le noeud courant est à sa place
# donc on arrête de tasser
if decalage != 0:
# Sinon un des fils est plus grand, donc on l'échange de place
index_plus_grand_fils = index * 2 + decalage
T[index], T[index_plus_grand_fils] = T[index_plus_grand_fils], T[index]
nouvel_index = index_plus_grand_fils
# Si le noeud a encore des fils, on continue de tasser
index_nouveau_fils_gauche = 2 * (nouvel_index) + 1
if index_nouveau_fils_gauche < len(T):
tasser(T, nouvel_index)
Le tamisage ou parfois entassement, appliqué à un nœud n dont les fils g et d vérifient tous les deux la condition de tas permet, par échange de n avec l’un des fils g ou d, puis tamisage du sous arbre représenté par le fils échangé, de transformer le sous arbre (n, g, d) en tas. Le coût de l’opération dans le pire des cas est de O(h-p(n)), où p(n) est la profondeur du nœud n et h la hauteur totale du tas (cette hauteur étant en logarithme du nombre de nœud, car on a affaire a un arbre presque complet).
Construction
Pour construire un tas à partir d'un arbre (implémenté comme un tableau), il suffit de le tasser successivement, en partant "en bas" de l'arbre, sans se préoccuper des feuilles :
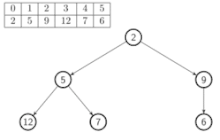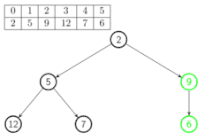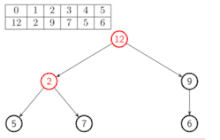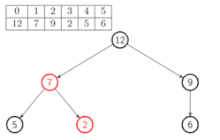
Pseudo-code :
Fonction construire_tas (T) T.taille= pour i allant de à 1 appeler tasser (T,i)
Python :
def construire_tas(T):
for i in range(len(T) // 2, 0, -1):
tasser(T, i)
La construction se fait en O(n), où n est le nombre total de nœuds.
Applications
La structure de tas possède possède de nombreuses applications pratiques, parmi lesquelles :
- Le tri par tas : un algorithme de tri qui peut être implémenté sur place avec une complexité asymptotique moyenne et dans le pire des cas linéarithmique, O(n ln n).
- En plus de permettre l'accès au plus petit ou plus grand élément, le tas permet aussi l'accès à d'autres éléments spécifiques tels que le médian ou le k-ième élément en un temps sous-linéaire en le nombre d'éléments du tas.
- La structure de tas est exploitée par divers algorithmes de parcours de graphes, tels que l'algorithme de Dijkstra ou la recherche d'un arbre couvrant minimal de Prim.
- Le tas se prête particulièrement à l'implémentation d'une file de priorité, en plaçant l'élément de plus forte priorité à sa racine.
Tri par tas
Quitte à devoir construire un arbre à partir des données en entrée (en O(n)), il est possible d’extraire le sommet du tas et de tamiser à la racine, en répétant l’opération jusqu’à avoir un tas vide. Les données en entrée sont alors triées dans l’ordre croissant en O(n log(n)) (complexité asymptotique optimale pour un tri) ; et une représentation en mémoire astucieuse (avec des tableaux de taille fixée) permet d’effectuer le tri sur place, c’est-à-dire sans allocation de mémoire supplémentaire autre que la pile d’exécution des récursions. Cependant, ce tri n’est pas stable, et sa complexité temporelle est en pratique inférieure à celle du tri rapide (quicksort).
Certaines implémentations permettent également la suppression d’éléments autres que le sommet, et la modification de la clef d’un élément. Il est possible d’implémenter ces opérations en O(log(n)), mais une structure de données annexe, permettant de retrouver la position d’un élément, doit être gérée pour éviter une recherche dans le tas, non optimisé pour ce genre d’opérations et susceptible de nécessiter O(n) opérations sans cette table annexe.
Implémentations
- La bibliothèque standard du C++ propose les primitives
make_heap,push_heapetpop_heapqui permettent la création de tas, l'insertion et l'extraction d'un élément respectivement. Les tas sont représentés en machine par des tableaux et la méthodepriority_queuepermet l'utilisation directe de la structure dans une file de priorité. En revanche, le catalogue ne permet pas de tamiser un élément ou d'en modifier la clé directement. - La bibliothèque boost de C++ étend l'implémentation des tas en permettant de modifier les clés et en introduisant les tas d-aires, binomiaux, les tas de Fibonacci et d'appariement.
- Java offre depuis sa version 1.5 une implémentation des tas binaires avec la classe
java.util.PriorityQueue. Seuls les tas-min sont disponibles nativement, pour avoir un tas-max, l'utilisateur devra définir son propre comparateur. Il n'est pas possible de tamiser un élément ou d'en modifier la clé directement. - Pour Python, le module
heapqimplémente une file de priorité par un tas binaire. - PHP propose à la fois le tas-min (
SplMinHeap) et le tas-max (SplMaxHeap) dans sa bibliothèque standard en version 5.3. - Perl apporte une implémentation de tas binaires, binomiaux et de Fibonacci avec la distribution Heap disponible depuis CPAN.
- Pour Pharo, une implémentation est disponible dans le module
Collections-Sequenceable, qui contient aussi un catalogue d'exemples. - Le langage Rust a une implémentation tas-max,
BinaryHeapest accessible depuis le modulecollectionsde sa bibliothèque standard.
Références
- (en) Thomas H. Cormen, Introduction to Algorithms, 1313 p. (lire en ligne), p. 151-169
- Robert Laganière, « CSI 2510 : Structure de données et algorithmes », sur site.uottawa.ca (consulté le )
- JWJ Williams, « Algorithm 232: Heapsort », Communication of the ACM, vol. 7, , p. 347–348 (lire en ligne, consulté le )
- Judicaël Courant, Arbres tournois, tas-max, , 7 p. (lire en ligne)

![{\displaystyle \displaystyle argmax_{j\in \left\{i,\left\lfloor {\frac {i}{2}}\right\rfloor \right\}\cap [\![1,...,T.taille]\!]}T[j]}](https://img.franco.wiki/i/849cf5b69f973b00e540d3cb5081e5d8940ac933.svg)

![T[i]](https://img.franco.wiki/i/aad46e2c555641e382521acf8f0a263ab284bb89.svg)
![{\displaystyle T[k]}](https://img.franco.wiki/i/846452de4084299705e8c3974e3f257c36907e0e.svg)

![{\displaystyle \displaystyle argmax_{j\in \{i,2i+1,2i+2\}\cap [\![1,...,T.taille]\!]}T[j]}](https://img.franco.wiki/i/f6cd20c5f4f93e5e00c70f0cb928d4d2d130809d.svg)


