Tri par sélection
Le tri par sélection (ou tri par extraction) est un algorithme de tri par comparaison. Cet algorithme est simple, mais considéré comme inefficace car il s'exécute en temps quadratique en le nombre d'éléments à trier, et non en temps pseudo linéaire.

| Problème lié | |
|---|---|
| Structure des données |
| Pire cas | |
|---|---|
| Moyenne | |
| Meilleur cas |
| Pire cas |
|---|
Description, pseudo-code et variantes
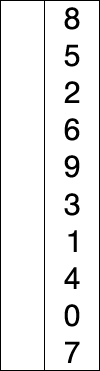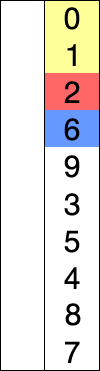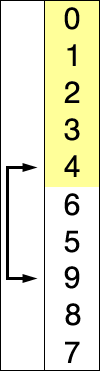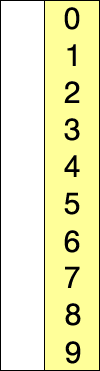
Sur un tableau de n éléments (numérotés de 0 à n-1 , attention un tableau de 5 valeurs (5 cases) sera numéroté de 0 à 4 et non de 1 à 5), le principe du tri par sélection est le suivant :
- rechercher le plus petit élément du tableau, et l'échanger avec l'élément d'indice 0 ;
- rechercher le second plus petit élément du tableau, et l'échanger avec l'élément d'indice 1 ;
- continuer de cette façon jusqu'à ce que le tableau soit entièrement trié.
En pseudo-code, l'algorithme s'écrit ainsi :
procédure tri_selection(tableau t)
n ← longueur(t)
pour i de 0 à n - 2
min ← i
pour j de i + 1 à n - 1
si t[j] < t[min], alors min ← j
fin pour
si min ≠ i, alors échanger t[i] et t[min]
fin pour
fin procédure
Une variante consiste à procéder de façon symétrique, en plaçant d'abord le plus grand élément à la fin, puis le second plus grand élément en avant-dernière position, etc.
Le tri par sélection peut aussi être utilisé sur des listes. Le principe est identique, mais au lieu de déplacer les éléments par échanges, on réalise des suppressions et insertions dans la liste.
Correction
L'invariant de boucle suivant permet de prouver la correction de l'algorithme : à la fin de l'étape i, le tableau est une permutation du tableau initial et les i premiers éléments du tableau coïncident avec les i premiers éléments du tableau trié.
Propriétés
Le tri par sélection est un tri en place (les éléments sont triés directement dans la structure).
Implémenté comme indiqué ci-dessus, ce n'est pas un tri stable (l'ordre d'apparition des éléments égaux n'est pas préservé). Toutefois, si l'on travaille sur une structure de données adaptée (typiquement une liste), il est facile de le rendre stable : à chaque itération, il convient de chercher la première occurrence de l'élément le plus petit de la partie non triée de la liste, et de l'insérer avant le premier élément de la partie non triée de la liste, plutôt que de l'échanger avec celui-ci. Implémentée sur un tableau, cette modification implique de décaler toute une partie du tableau à chaque itération, et n'est donc pas intéressante.
Cela dit, il est possible d'optimiser le processus aux travers de la création d'une nouvelle liste. Evitant ainsi de décaler le tableau à chaque itération.
Complexité
Dans tous les cas, pour trier n éléments, le tri par sélection effectue comparaisons. Sa complexité est donc Θ(n2). De ce point de vue, il est inefficace puisque les meilleurs algorithmes[1] s'exécutent en temps . Il est même moins bon que le tri par insertion ou le tri à bulles, qui sont aussi quadratiques dans le pire cas mais peuvent être plus rapides sur certaines entrées particulières.
Par contre, le tri par sélection effectue au plus un nombre linéaire d'échanges :
- n-1 échanges dans le pire cas, qui est atteint par exemple lorsqu'on trie la séquence 2,3,…,n,1 ;
- en moyenne[2], c'est-à-dire si les éléments sont deux à deux distincts et que toutes leurs permutations sont équiprobables (en effet, l'espérance du nombre d'échanges à l'étape i est ) ;
- aucun si l'entrée est déjà triée.
Ce tri est donc intéressant lorsque les éléments sont aisément comparables, mais coûteux à déplacer dans la structure.
Références
- Voir par exemple tri fusion, tri rapide et tri par tas.
- (en) Donald E. Knuth, The Art of Computer Programming, vol. 3 : Sorting and Searching, , 2e éd. [détail de l’édition], section 5.2.3, exercice 4.
Voir aussi
Articles connexes
- Algorithme de sélection
- Mélange de Fisher-Yates, algorithme de mélange pouvant être vu comme l'inverse du tri par sélection.





