Mélange de Fisher-Yates

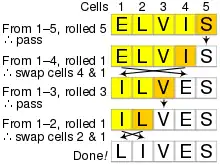
Pour mélanger un tableau a de n éléments (indicés de 0 à n-1), l'algorithme est le suivant.

 Pour i allant de n − 1 à 1 faire :
       j ← entier aléatoire entre 0 et i
       échanger a[j] et a[i]

Cet algorithme a une complexité linéaire et donne toutes les permutations avec la même probabilité. Au k-ième pas il y a n-k choix possibles, donc il y a n! déroulements possibles, de plus l'élément placé en k au pas k ne sera plus jamais modifié dans les pas suivants, ce qui prouve que toutes les permutations seront générées, et avec égale probabilité. Il peut être vu comme un tri par sélection inversé[1].

L'algorithme apparait la première fois dans un ouvrage de Fisher et Yates[2] en 1938. Il est redécouvert sous une forme plus algorithmique par Richard Durstenfeld en 1964[3], puis popularisé par Donald Knuth sous le nom d'algorithme P[4].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Fisher–Yates shuffle » (voir la liste des auteurs).

• Jeff Atwood, « The Danger of Naïveté », sur Coding Horror (Une comparaison de l'algorithme naïf et de l'algorithme de Fisher-Yates)
• Mike Bostock, « Fisher–Yates Shuffle » (Visualisation de différents mélanges)