Tri fusion
En informatique, le tri fusion, ou tri dichotomique, est un algorithme de tri par comparaison stable. Sa complexité temporelle pour une entrée de taille n est de l'ordre de n log n, ce qui est asymptotiquement optimal. Ce tri est basé sur la technique algorithmique diviser pour régner. L'opération principale de l'algorithme est la fusion, qui consiste à réunir deux listes triées en une seule. L'efficacité de l'algorithme vient du fait que deux listes triées peuvent être fusionnées en temps linéaire.
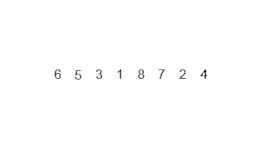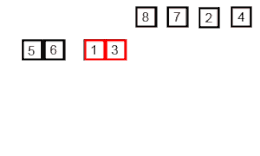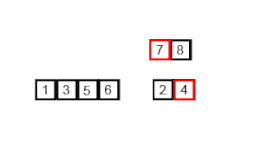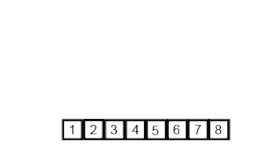
| Découvreur ou inventeur | |
|---|---|
| Date de découverte | |
| Problèmes liés | |
| Structures des données | |
| À l'origine de |
| Pire cas | |
|---|---|
| Moyenne | |
| Meilleur cas |
| Pire cas | |
|---|---|
| Meilleur cas |
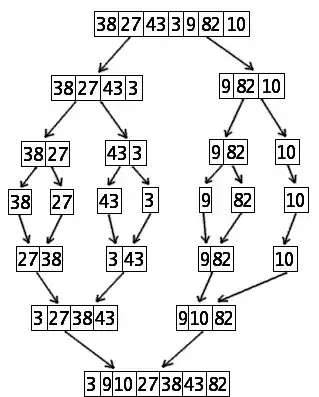
Le tri fusion se décrit naturellement sur des listes et c'est sur de telles structures qu'il est à la fois le plus simple et le plus rapide. Cependant, il fonctionne aussi sur des tableaux. La version la plus simple du tri fusion sur les tableaux a une efficacité comparable au tri rapide, mais elle n'opère pas en place : une zone temporaire de données supplémentaire de taille égale à celle de l'entrée est nécessaire (des versions plus complexes peuvent être effectuées sur place mais sont moins rapides). Sur les listes, sa complexité est optimale, il s'implémente très simplement et ne requiert pas de copie en mémoire temporaire.
Intuition
À partir de deux listes triées, on peut facilement construire une liste triée comportant les éléments issus de ces deux listes (leur fusion). Le principe de l'algorithme de tri fusion repose sur cette observation : le plus petit élément de la liste à construire est soit le plus petit élément de la première liste, soit le plus petit élément de la deuxième liste. Ainsi, on peut construire la liste élément par élément en retirant tantôt le premier élément de la première liste, tantôt le premier élément de la deuxième liste (en fait, le plus petit des deux, à supposer qu'aucune des deux listes ne soit vide, sinon la réponse est immédiate).
Ce procédé est appelé fusion et est au cœur de l'algorithme de tri développé ci-après.
Algorithme

L'algorithme est naturellement décrit de façon récursive.
- Si le tableau n'a qu'un élément, il est déjà trié.
- Sinon, séparer le tableau en deux parties à peu près égales.
- Trier récursivement les deux parties avec l'algorithme du tri fusion.
- Fusionner les deux tableaux triés en un seul tableau trié.
En pseudo-code :
entrée : un tableau T
sortie : une permutation triée de T
fonction triFusion(T[1, …, n])
si n ≤ 1
renvoyer T
sinon
renvoyer fusion(triFusion(T[1, …, n/2]), triFusion(T[n/2 + 1, …, n]))
entrée : deux tableaux triés A et B
sortie : un tableau trié qui contient exactement les éléments des tableaux A et B
fonction fusion(A[1, …, a], B[1, …, b])
si A est le tableau vide
renvoyer B
si B est le tableau vide
renvoyer A
si A[1] ≤ B[1]
renvoyer A[1] ⊕ fusion(A[2, …, a], B)
sinon
renvoyer B[1] ⊕ fusion(A, B[2, …, b])
L'algorithme se termine car la taille du tableau à trier diminue strictement au fil des appels. La fusion de A et B est en où a est la taille de A et b est la taille de B. Le tri fusion d'un tableau T est en où n est la taille du tableau T. Le symbole ⊕ désigne ici la concaténation de tableaux.
Mise en œuvre sur des listes
L'algorithme suivant est détaillé de sorte qu'il soit traduisible en n'importe quel langage impératif. La liste à trier est de taille n. Pour la concision et l'efficacité de l'algorithme, on suppose que la liste à trier comporte au moins 2 éléments et que :
- soit elle est simplement chaînée, non circulaire et précédée par un maillon racine p (hors de la liste mais pointant vers son premier élément) ;
- soit elle est simplement chaînée et circulaire ;
- soit elle est doublement chaînée et circulaire.
Dans tous les cas, la liste est triée après le chaînon p passé en paramètre, c'est-à-dire que le chainon successeur de p sera le plus petit de la liste. Des descriptions un peu moins concises mais libérées de ces contraintes structurelles existent.
fonction trier(p, n)
Q := n/2 (division entière)
P := n-Q
si P >= 2
q := trier(p, P)
si Q >= 2
trier(q, Q)
sinon
q := p.suivant
fin
q := fusionner(p, P, q, Q)
renvoyer q
fin
fonction fusionner(p, P, q, Q)
pour i allant de 0 à taille(p)-1 faire
si valeur(p.suivant) > valeur(q.suivant)
déplacer le maillon q.suivant après le maillon p
si Q = 1 quitter la boucle
Q := Q-1
sinon
si P = 1
tant que Q >= 1
q := q.suivant
Q := Q-1
fin
quitter la boucle
fin
P := P-1
fin
p := p.suivant
fin
renvoyer q
fin
Le déplacement d'un maillon q.suivant après un maillon p nécessite un pointeur temporaire t. Si la liste est simplement chainée, le déplacement se fait par cet échange de liens :
t := q.suivant
q.suivant := t.suivant
t.suivant := p.suivant
p.suivant := t
Si la liste est doublement chainée et circulaire, le déplacement se fait par cet échange de liens :
t := q.suivant
q.suivant := t.suivant
q.suivant.précédent := q
t.précédent := p
t.suivant := p.suivant
p.suivant.précédent := t
p.suivant := t
Ainsi décrit, l'algorithme peut être hybridé très facilement avec d'autres tris. Cela se fait en rajoutant une condition sur la toute première ligne de la fonction trier(p, n). Sur de petites sous-listes, elle a pour rôle de remplacer toutes les opérations qui suivent par un tri de complexité quadratique mais en pratique plus rapide. Dans la suite, les conditions P >= 2 et Q >= 2 peuvent alors être retirées.
Mise en œuvre sur des tableaux
Avec des tableaux, on peut faire le tri sur place ou non. On a alors schématiquement trois possibilités de gestion de la mémoire :
- On fait le traitement sur place. On commence par trier les paires ou les triades d'éléments sur place puis on fusionne sur place les listes adjacentes entre elles. La procédure de fusion s'applique alors à un sous-tableau contenant deux listes l'une après l'autre. Pour fusionner en place, la mise en œuvre simple, qui consiste à décaler la première liste quand on insère un ou plusieurs éléments de la deuxième, est lente (un peu comme un tri par insertion). D'autres algorithmes plus rapides existent, mais ils sont compliqués et souvent ne sont pas stables (ne conservent pas l'ordre précédent). Voir le lien externe plus bas.
- On fait le traitement à moitié sur place. On commence par trier les paires ou les triades d'éléments sur place puis on fusionne. Lors de la fusion, on effectue une copie de la première liste en mémoire temporaire (on peut faire une copie des deux listes, mais ce n'est pas nécessaire). Ainsi on n'a plus besoin de décaler les données, on copie simplement un élément de la première liste (depuis la mémoire temporaire) ou de la deuxième liste (qui est gardée sur place). Cette solution est plus rapide (plus rapide qu'un tri par tas mais plus lente qu'un tri rapide).
- On utilise une zone temporaire de même taille que le tableau à trier. On peut alors faire les fusions d'un des tableaux à l'autre. Trier un seul élément revient alors à le recopier d'un tableau à l'autre, trier deux éléments revient à les copier de manière croisée ou non etc. Cette fois, lors de la fusion, quand on copie le premier élément de la première liste ou de la deuxième, on n'a pas besoin de décaler les données, ni de recopier la première liste. Cette solution a une complexité comparable au tri rapide, sans avoir l'inconvénient du pire des cas quadratique. Ce tri fusion fait plus de copies qu'un tri rapide mais fait moins de comparaisons.
Propriétés
- Le nombre de comparaisons nécessaires est de l'ordre de .
- L'espace mémoire requis est en O(n) à moins de faire des rotations d'éléments.
Optimisations possibles
- Au niveau de l'utilisation de la mémoire :
- On peut limiter la mémoire utilisée à n/2 éléments en recopiant seulement la première des deux listes à fusionner en mémoire temporaire ;
- On peut limiter la mémoire utilisée à O(1) en ne recopiant pas les éléments. On peut fusionner en faisant une rotation des éléments allant du milieu de la première liste au milieu de la deuxième.
- Au niveau de la vitesse d'exécution :
- On peut avoir la rapidité d'exécution de la copie d'un tableau à un autre, tout en utilisant un tableau temporaire de taille n/2 seulement. Soit A la première et B la deuxième moitié du tableau à trier, et C le tableau temporaire de taille n/2. On trie en copiant les éléments entre A et C, puis entre A et B. Enfin, on fusionne les listes obtenues en B et C dans le tableau entier AB.
Exemple
Opération de fusion
Fusionner [1;2;5] et [3;4] : le premier élément de la liste fusionnée sera le premier élément d'une des deux listes d'entrée (soit 1, soit 3) car ce sont des listes triées.
- Comparer 1 et 3 : 1 est plus petit
- [2;5] - [3;4] → [1]
- Comparer 2 et 3 : 2 est plus petit
- [5] - [3;4] → [1;2]
- Compare 5 et 3 → 3 est plus petit
- [5] - [4] → [1;2;3]
- Compare 5 et 4 : 4 est plus petit
- [5] → [1;2;3;4]
- Résultat de la fusion :
- [1;2;3;4;5]
Tri, procédure complète
Déroulons les appels successifs de tri_fusion([6, 1, 2, 5, 4, 7, 3]) :
tri_fusion([6, 1, 2, 5, 4, 7, 3])
[6, 1, 2, 5] [4, 7, 3]
tri_fusion([6, 1, 2, 5])
[6, 1] [2, 5]
tri_fusion([6, 1])
[6] [1]
tri_fusion([6])
--> [6]
tri_fusion([1])
--> [1]
'''fusion''' de [6] et [1] : [1, 6]
--> [1, 6]
tri_fusion([2, 5])
[2] [5]
tri_fusion([2])
--> [2]
tri_fusion([5])
--> [5]
'''fusion''' de [2] et [5] : [2, 5]
--> [2, 5]
'''fusion''' de [1, 6] et [2, 5] : [1, 2, 5, 6]
--> [1, 2, 5, 6]
tri_fusion([4, 7, 3])
[4] [7, 3]
tri_fusion([4])
--> [4]
tri_fusion([7, 3])
[7] [3]
tri_fusion([7])
--> [7]
tri_fusion([3])
--> [3]
'''fusion''' de [7] et [3] : [3, 7]
--> [3, 7]
'''fusion''' de [4] et [3, 7] : [3, 4, 7]
--> [3, 4, 7]
'''fusion''' de [1, 2, 5, 6] et [3, 4, 7] : [1, 2, 3, 4, 5, 6, 7]
--> [1, 2, 3, 4, 5, 6, 7]
On peut remarquer que la fonction de fusion est toujours appelée sur des listes triées.
Voir aussi
Liens externes
- (en) Java utilise une variante du tri fusion pour ses tris de l'objet Collections
- (en) Tri fusion sur place : un article sur un tri fusion sur place mais pas stable en (fichier au format PostScript)
- (en) Tri fusion sur place : algorithme astucieux en Java de tri fusion en place et stable, utilisant des rotations d'éléments
- (en) Illustration dynamique du tri fusion
Références
- Steven Skiena, The Algorithm Design Manual, Springer Science+Business Media, , 730 p. (ISBN 978-1-84800-069-8), p. 122




