Tri par insertion
En informatique, le tri par insertion est un algorithme de tri classique. La plupart des personnes l'utilisent naturellement pour trier des cartes à jouer[1].

| Problèmes liés |
Algorithme de tri, tri stable (en), tri par comparaison (en), adaptive sort (en), algorithme en place (en), algorithme en ligne |
|---|---|
| Structure des données | |
| À l'origine de |
| Pire cas | |
|---|---|
| Moyenne | |
| Meilleur cas |
| Pire cas |
|---|
En général, le tri par insertion est beaucoup plus lent que d'autres algorithmes comme le tri rapide (ou quicksort) et le tri fusion pour traiter de grandes séquences, car sa complexité asymptotique est quadratique.
Le tri par insertion est cependant considéré comme l'algorithme le plus efficace sur des entrées de petite taille. Il est aussi efficace lorsque les données sont déjà presque triées. Pour ces raisons, il est utilisé en pratique en combinaison avec d'autres méthodes comme le tri rapide.
En programmation informatique, on applique le plus souvent ce tri à des tableaux. La description et l'étude de l'algorithme qui suivent se restreignent à cette version, tandis que l'adaptation à des listes est considérée plus loin.
Description
Le tri par insertion considère chaque élément du tableau et l'insère à la bonne place parmi les éléments déjà triés. Ainsi, au moment où on considère un élément, les éléments qui le précèdent sont déjà triés, tandis que les éléments qui le suivent ne sont pas encore triés.
Pour trouver la place où insérer un élément parmi les précédents, il faut le comparer à ces derniers, et les décaler afin de libérer une place où effectuer l'insertion. Le décalage occupe la place laissée libre par l'élément considéré. En pratique, ces deux actions s'effectuent en une passe, qui consiste à faire « remonter » l'élément au fur et à mesure jusqu'à rencontrer un élément plus petit.
Le tri par insertion est un tri stable (conservant l'ordre d'apparition des éléments égaux) et un tri en place (il n'utilise pas de tableau auxiliaire).
L'algorithme a la particularité d'être online, c'est-à-dire qu'il peut recevoir la liste à trier élément par élément sans perdre en efficacité.
Exemple
Voici les étapes de l'exécution du tri par insertion sur le tableau [6, 5, 3, 1, 8, 7, 2, 4]. Le tableau est représenté au début et à la fin de chaque itération.
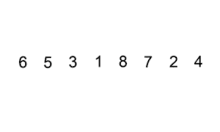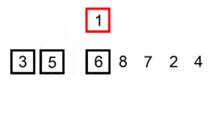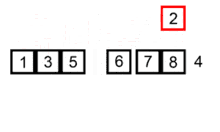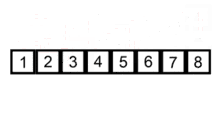
| i = 1 : |
|
⟶ |
| ||||||||||||||||
| i = 2 : |
|
⟶ |
| ||||||||||||||||
| i = 3 : |
|
⟶ |
| ||||||||||||||||
| i = 4 : |
|
⟶ |
| ||||||||||||||||
| i = 5 : |
|
⟶ |
| ||||||||||||||||
| i = 6 : |
|
⟶ |
| ||||||||||||||||
| i = 7 : |
|
⟶ |
|
Pseudo-code
Voici une description en pseudo-code de l'algorithme présenté. Les éléments du tableau T (de taille n) sont numérotés de 0 à n-1.
procédure tri_insertion(tableau T)
pour i de 1 à taille(T) - 1
# mémoriser T[i] dans x
x ← T[i]
# décaler les éléments T[0]..T[i-1] qui sont plus grands que x, en partant de T[i-1]
j ← i
tant que j > 0 et T[j - 1] > x
T[j] ← T[j - 1]
j ← j - 1
# placer x dans le "trou" laissé par le décalage
T[j] ← x
Complexité
La complexité du tri par insertion est Θ(n2) dans le pire cas et en moyenne, et linéaire dans le meilleur cas. Plus précisément :
- Dans le pire cas, atteint lorsque le tableau est trié à l'envers, l'algorithme effectue de l'ordre de n2/2 affectations et comparaisons[2] ;
- Si les éléments sont distincts et que toutes leurs permutations sont équiprobables (ie avec une distribution uniforme), la complexité en moyenne de l'algorithme est de l'ordre de n2/4 affectations et comparaisons[2] ;
- Si le tableau est déjà trié, il y a n-1 comparaisons et au plus n affectations.
La complexité du tri par insertion reste linéaire si le tableau est presque trié (par exemple, chaque élément est à une distance bornée de la position où il devrait être, ou bien tous les éléments sauf un nombre borné sont à leur place). Dans cette situation particulière, le tri par insertion surpasse d'autres méthodes de tri : par exemple, le tri fusion et le tri rapide (avec choix aléatoire du pivot) sont tous les deux en même sur une liste triée.
Variantes et optimisations
Optimisations pour les tableaux
Plusieurs modifications de l'algorithme permettent de diminuer le temps d'exécution, bien que la complexité reste quadratique.
- On peut optimiser ce tri en commençant par un élément au milieu de la liste puis en triant alternativement les éléments après et avant. On peut alors insérer le nouvel élément soit à la fin, soit au début des éléments triés, ce qui divise par deux le nombre moyen d'éléments décalés. Il est possible d'implémenter cette variante de sorte que le tri soit encore stable.
- En utilisant une recherche par dichotomie pour trouver l'emplacement où insérer l'élément, on peut ne faire que comparaisons. Le nombre d'affectations reste en O(n2).
- L'insertion d'un élément peut être effectuée par une série d'échanges plutôt que d'affectations. En pratique, cette variante peut être utile dans certains langages de programmation (par exemple C++), où l'échange de structures de données complexes est optimisé, alors que l'affectation provoque l'appel d'un constructeur de copie (en).
Le tri de Shell est une variante du tri par insertion qui améliore sa complexité asymptotique, mais n'est pas stable.
Tri par insertion sur des listes
Le principe du tri par insertion peut être adapté à des listes chaînées. Dans ce cas, le déplacement de chaque élément peut se faire en temps constant (une suppression et un ajout dans la liste). Par contre, le nombre de comparaisons nécessaires pour trouver l'emplacement où insérer reste de l'ordre de n²/4, la méthode de recherche par dichotomie ne pouvant pas être appliquée à des listes.
Combinaison avec d'autres tris
En pratique, sur les petites entrées, en dessous d'une taille critique K (qui dépend de l'implémentation et de la machine utilisée), les algorithmes de tri en basés sur la méthode « diviser pour régner » (tri fusion, tri rapide) sont moins efficaces que le tri par insertion. Dans ce type d'algorithmes, plutôt que de diviser récursivement l'entrée jusqu'à avoir des sous-problèmes élémentaires de taille 1 ou 2, on peut s'arrêter dès que les sous-problèmes ont une taille inférieure à K et les traiter avec le tri par insertion.
Pour le cas particulier du tri rapide, une variante plus efficace existe[3] :
- exécuter d'abord le tri rapide en ignorant simplement les sous-problèmes de taille inférieure à K ;
- faire un tri par insertion sur le tableau complet à la fin, ce qui est rapide car la liste est déjà presque triée.
Voir aussi
Notes et références
- (en) Sedgewick, Robert, Algorithms., Addison-Wesley, (ISBN 978-0-201-06672-2), p. 95
- (en) Donald E. Knuth, The Art of Computer Programming, vol. 3 : Sorting and Searching, , 2e éd. [détail de l’édition], section 5.2.1.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction à l'algorithmique, Dunod, [détail de l’édition] (ex. 7.4.5, p. 153)




