Apprentissage non supervisé

Différence entre les deux types d'apprentissage.

• On dispose d'éléments déjà classés

Exemple : articles en rubrique cuisine, sport, culture...

Différence entre les deux types d'apprentissage.

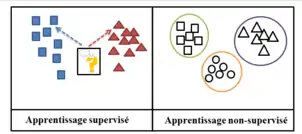
• On veut classer un nouvel élément

Exemple : lui attribuer un nom parmi cuisine, sport, culture...

• On dispose d'éléments non classés

Exemple : une fleur

• On veut les regrouper en classes

Exemple : si deux fleurs ont la même forme, elles sont en rapport avec une même plante correspondante.

Il existe deux principales méthodes d'apprentissage non supervisées[4] :

• Les méthodes par partitionnement telles que les algorithmes des k-moyennes ou k-médoïdes.
• Les méthodes de regroupement hiérarchique.

Le clustering consiste à grouper des points de données en fonction de leurs similitudes, tandis que l’association consiste à découvrir des relations entre les attributs de ces points de données:

Les techniques de clustering cherchent à décomposer un ensemble d'individus en plusieurs sous ensembles les plus homogènes possibles

• On ne connaît pas la classe des exemples (nombre, forme, taille)

• Les méthodes sont très nombreuses, typologies généralement employées pour les distinguer Méthodes de partitionnement / Méthodes hiérarchiques

• Avec recouvrement / sans recouvrement

• Autre : incrémental / non incrémental

• D'éventuelles informations sur les classes ou d'autres informations sur les données n'ont pas d'influence sur la formation des clusters, seulement sur leur interprétation[7].

L'un des algorithmes le plus connu et utilisé en clustering est la K-moyenne. Cet algorithme va mettre dans des “zones” (Cluster), les données qui se ressemblent. Les données se trouvant dans le même cluster sont similaires.

L’approche de K-Means consiste à affecter aléatoirement des centres de clusters (appelés centroids), et ensuite assigner chaque point de nos données au centroid qui lui est le plus proche. Cela s’effectue jusqu’à assigner toutes les données à un cluster[8].

Tendance pour une tâche à utiliser des méthodes supervisées ou non supervisées. Les noms de tâches chevauchant les limites du cercle sont intentionnels. Il montre que la division classique des tâches imaginatives (à gauche) utilisant des méthodes non supervisées est floue dans les schémas d'apprentissage d'aujourd'hui.

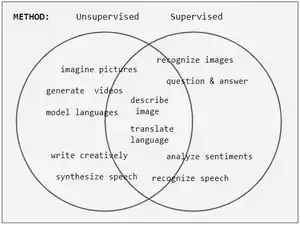
Les tâches du réseau de neurones sont souvent classées comme discriminatives (reconnaissance) ou génératives (imagination). Les tâches discriminatives utilisent souvent (mais pas toujours) des méthodes supervisées et les tâches génératives utilisent des méthodes non supervisées (voir diagramme de Venn); cependant, la séparation est très floue. Par exemple, la reconnaissance d'objets favorise l'apprentissage supervisé, mais l'apprentissage non supervisé peut également regrouper des objets en groupes. De plus, au fur et à mesure que des progrès, certaines tâches utilisent les deux méthodes, et certaines tâches oscillent de l'une à l'autre. Par exemple, la reconnaissance d'images a commencé comme étant fortement supervisée, mais est devenue hybride en employant un pré-entrainement non supervisée, puis est revenue à la supervision avec l'avènement de l'abandon, de ReLU et des taux d'apprentissage adaptatifs.

Pendant la phase d'apprentissage, un réseau non supervisé essaie d'imiter les données qui lui sont fournies et utilise l'erreur dans sa sortie imitée pour se corriger (c'est-à-dire corriger ses poids et ses biais). Parfois, l'erreur est exprimée comme une faible probabilité que la sortie erronée se produise, ou elle peut être exprimée comme un état de haute énergie instable dans le réseau.

Contrairement à l'utilisation dominante de la rétropropagation par les méthodes supervisées, l'apprentissage non supervisé utilise également d'autres méthodes, notamment : la règle d'apprentissage de Hopfield, la règle d'apprentissage de Boltzmann, la divergence contrastive, le sommeil éveillé, l'inférence variationnelle, la vraisemblance maximale, le maximum A Posteriori, l'échantillonnage de Gibbs, et la rétropropagation des erreurs de reconstruction ou des reparamétrisations d'état caché. Voir le tableau ci-dessous pour plus de détails.

Une fonction énergétique est une mesure macroscopique de l'état d'activation d'un réseau. Dans les machines Boltzmann, il joue le rôle de la fonction de coût. Cette analogie avec la physique est inspirée de l'analyse par Ludwig Boltzmann de l'énergie macroscopique d'un gaz à partir des probabilités microscopiques du mouvement des particules ${\displaystyle p\propto e^{-{\frac {E}{kT}}}}$, où k est le Constante de Boltzmann et T est la température. Dans le réseau RBM, la relation est ${\displaystyle p={\frac {e^{-E}}{Z}}}$[9], où p & E varient sur chaque schéma d'activation possible et ${\displaystyle Z=\sum _{\text{tout les patterns}}e^{-E(pattern)}}$. Pour être plus précis, ${\displaystyle p(a)={\frac {e^{-E}}{Z}}}$, où a est un modèle d'activation de tous les neurones (visibles et cachés). Par conséquent, les premiers réseaux de neurones portent le nom de Boltzmann Machine. Paul Smolensky appelle ${\displaystyle -E}$ l'Harmonie. Un réseau cherche énergie basse qui correspond à une Harmonie haute.

Nous soulignons ici certaines caractéristiques de certains réseaux. Des détails sont également donnés dans le tableau comparatif ci-dessous. Au fur et à mesure que la conception des réseaux change, des fonctionnalités sont ajoutées pour activer de nouvelles fonctionnalités ou supprimées pour accélérer l'apprentissage. Par exemple, les neurones changent entre déterministe (Hopfield) et stochastique (Boltzmann) pour permettre une sortie robuste, les poids sont supprimés dans une couche (RBM) pour accélérer l'apprentissage, ou les connexions peuvent devenir asymétriques (Helmholtz). Les connexion symétriques permettent une formulation énergétique globale.

Notations

Un réseaux est composé de ${\displaystyle N}$ neurones, on note la matrice de connexion du réseau ${\displaystyle W=(w_{i,j})_{1\leq i\leq n,1\leq j\leq n}}$, l'énergie du réseaux ${\displaystyle E}$.

Réseau Hopfield

Publication	1982[10]
Neurone	Neurone formel binaire ${\displaystyle s_{i}\leftarrow \left\{{\begin{array}{ll}+1&{\text{si }}\sum _{j}{w_{ij}V_{j}}\geq \theta _{i}\\-1&{\text{sinon.}}\end{array}}\right.}$ ${\displaystyle V_{i}}$ est l'état de du neurone ${\displaystyle i}$ ${\displaystyle \theta _{i}}$ est le seuil du neurone ${\displaystyle i}$
Énergie	${\displaystyle E=-{\frac {1}{2}}\sum _{i,j}{w_{ij}{V_{i}}{V_{j}}}+\sum _{i}{\theta _{i}}{V_{i}}}$
Formation	${\displaystyle w_{ij}={\frac {1}{p}}\sum _{k=1}^{p}x_{i}^{k}x_{j}^{k}\,}$ avec : ${\displaystyle p}$ le nombre de motif d'entraînement ${\displaystyle x_{i}^{k}}$ est la valeur du neurone ${\displaystyle i}$ pour le motif ${\displaystyle k}$

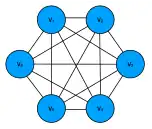
Un réseau basé sur des domaines magnétiques dans le fer avec une seule couche auto-connectée. Il peut être utilisé comme mémoire adressable par le contenu. Un neurone correspond à un domaine de fer avec des moments magnétiques binaires Up et Down, et les connexions neuronales correspondent à l'influence des domaines les uns sur les autres.

Un réseaux est composé de neurones binaires dont l'état ${\displaystyle V_{i}\in \{-1,1\}}$ ou ${\displaystyle V_{i}\in \{0,1\}}$ pour le neurone ${\displaystyle i}$. On apprend aux réseaux les motifs ${\displaystyle x^{k}\in \mathbb {R} ^{N}}$, ${\displaystyle 1\leq k\leq p}$. Pendant l'inférence, on présente au réseau des motifs appris mais incomplet ou bruité, le réseau met à jour chaque état en utilisant la fonction d'activation standard et conduit à un état appris.

Des poids symétriques et les bonnes fonctions d'énergie garantissent la convergence vers un modèle d'activation stable. Les poids asymétriques sont difficiles à analyser. Les réseaux Hopfield sont utilisés comme des mémoires adressables par le contenu (CAM).

Machine de Boltzmann

Publication	1975[11]
Neurone	Les probabilité d'activation sont données par : ${\displaystyle p_{\text{i=activé}}={\frac {1}{1+\exp(-{\frac {\Delta E_{i}}{T}})}}}$avec : ${\displaystyle \Delta E_{i}=\sum _{j>i}w_{ij}\,s_{j}+\sum _{j<i}w_{ji}\,s_{j}+\theta _{i}}$
Énergie	${\displaystyle E=-{\frac {1}{2}}\sum _{i,j}{w_{ij}{s_{i}}{s_{j}}}+\sum _{i}{\theta _{i}}{s_{i}}}$
Formation	minimiser la divergence KL ${\displaystyle \Delta w_{ij}=e\cdot (p_{ij}-p'_{ij})}$ avec : e = taux d'apprentissage, p' = distribution prédite et p = distribution réelle.

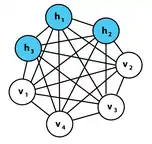
Un réseaux est composé de neurones stochastiques, d'état ${\displaystyle s_{i}\in \{0,1\}}$ pour le neurone ${\displaystyle i}$ et dont la probabilité d'activation dépend des activations des autres neurones. Il est séparé en 2 couches (caché vs visible), mais utilise toujours des poids symétriques à 2 voies. Les neurones visibles reçoivent l'entrée qui sont des vecteurs aux valeurs binaires.

Leur valeur d'état est échantillonnée à partir de cette densité de probabilité comme suit : supposons qu'un neurone binaire se déclenche avec une probabilité de Bernoulli ${\displaystyle p(1)=1/3}$ et se repose avec ${\displaystyle p(0)=2/3}$. On échantillonne dans ce dernier en prenant un nombre aléatoire uniformément distribué y, et en le plaçant dans la fonction de distribution cumulative inverse, qui dans ce cas est la fonction seuil à 2/3. La fonction inverse ${\displaystyle \left\{{\begin{array}{cc}0&{\text{si }}x\leq {\frac {2}{3}}\\1&{\text{si }}x>{\frac {2}{3}}\end{array}}\right.}$

Suivant la thermodynamique de Boltzmann, les probabilités individuelles donnent lieu à des énergies macroscopiques.

Machine de Boltzmann restreinte

Publications	1986[12], 2002[13]
Neurone	Les probabilité d'activation sont donnée par : ${\displaystyle P(h_{j}=1|v)=\sigma \left(b_{j}+\sum _{i=1}^{m}w_{i,j}v_{i}\right)}$ ${\displaystyle \,P(v_{i}=1|h)=\sigma \left(c_{i}+\sum _{j=1}^{n}w_{i,j}h_{j}\right)}$ avec ${\displaystyle \sigma }$ la fonction sigmoïde, ${\displaystyle b_{i}}$ et ${\displaystyle c_{j}}$ respectivement les biais des neurones ${\displaystyle v_{i}}$ et ${\displaystyle h_{j}}$.
Énergie	${\displaystyle E=-\sum _{i,j}w_{ij}\,v_{i}\,h_{j}-\sum _{i}b_{i}\,v_{i}-\sum _{j}c_{j}h_{j}}$
Formation	Algorithme de divergence contrastive: ${\displaystyle \Delta w_{ij}=e\cdot \left(\left\langle v_{i}h_{j}\right\rangle _{\text{données}}-\left\langle v_{i}h_{j}\right\rangle _{\text{équilibre}}\right)}$ où ${\displaystyle <>}$ désigne des moyennes

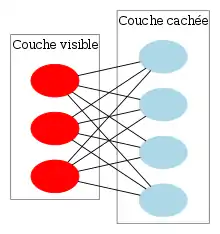
Il s'agit d'une machine Boltzmann où les connexions latérales au sein d'une couche sont interdites. On a donc à nouveau des neurones stochastiques, d'état ${\displaystyle v_{i}\in \{0,1\}}$ pour le neurone ${\displaystyle i}$ de la couche visible et ${\displaystyle h_{i}\in \{0,1\}}$ pour le neurone ${\displaystyle i}$ de la couche caché.

Le réseaux est entrainé pour maximiser produit des probabilité ${\displaystyle \prod _{j=1}^{N}=P(v_{j})}$.

Les machines de Boltzmann "non restreintes" peuvent avoir des connexions entre les unités cachées. Cette restriction permet d'utiliser des algorithmes d'apprentissage plus efficaces que ceux disponibles pour la classe générale des machines de Boltzmann, en particulier l'algorithme de divergence contrastive basé sur le gradient

Réseau de croyance sigmoïde

Énergie	${\displaystyle E=-{\frac {1}{2}}\sum _{i,j}{w_{ij}{s_{i}}{s_{j}}}+\sum _{i}{\theta _{i}}{s_{i}}}$
Formation	${\displaystyle \Delta w_{ij}=s_{i}\cdot s_{j}}$, pour +1/-1 neurone

Introduit par Radford Neal en 1992, ce réseau applique les idées des modèles graphiques probabilistes aux réseaux neuronaux. La principale différence réside dans le fait que les nœuds des modèles graphiques ont des significations pré-attribuées, alors que les caractéristiques des neurones du Belief Net sont déterminées après la formation. Le réseau est un graphe acyclique dirigé faiblement connecté composé de neurones stochastiques binaires. La règle d'apprentissage provient du maximum de vraisemblance sur ${\displaystyle p(X):\Delta w_{ij}\propto s_{j}\cdot (s_{i}-p_{i})}$, où ${\displaystyle p_{i}={\frac {1}{1+e^{\text{entrées pondérées du neurone i }}}}}$ Les ${\displaystyle s_{j}}$ sont des activations provenant d'un échantillon non biaisé de la distribution postérieure, ce qui pose problème en raison du problème d'explication de l'éloignement soulevé par Judea Perl. Les méthodes bayésiennes variationnelles utilisent un postérieur de substitution et ignorent manifestement cette complexité.

Réseau de croyance profond et machine de Boltzman restreintes empilés

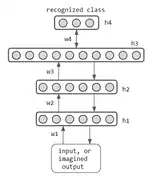
Introduit par Hinton, ce réseau est un hybride de RBM et de réseau de croyance sigmoïde. Les deux couches supérieures sont un RBM et la deuxième couche vers le bas forme un réseau de croyance sigmoïde. On l'entraîne par la méthode du RBM empilé, puis on jette les poids de reconnaissance sous le RBM supérieur. En 2009, 3-4 couches semblent être la profondeur optimale[14].

Ce réseau comporte plusieurs RBM pour coder une hiérarchie de caractéristiques cachées. Après la formation d'un seul RBM, une autre couche cachée bleue (voir RBM de gauche) est ajoutée, et les deux couches supérieures sont formées comme un RBM rouge et bleu.

Machine de Helmholtz

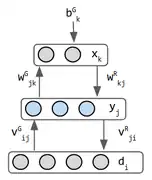
Au lieu de la connexion symétrique bidirectionnelle des machines Boltzmann empilées, nous avons des connexions unidirectionnelles séparées pour former une boucle. Il fait à la fois génération et discrimination.

Ce sont les premières inspirations des encodeurs automatiques variationnels. Il s'agit de 2 réseaux combinés en un seul - les poids vers l'avant opèrent la reconnaissance et les poids vers l'arrière mettent en œuvre l'imagination. C'est peut-être le premier réseau à faire les deux. Helmholtz n'a pas travaillé dans l'apprentissage automatique mais il a inspiré la vision d'un "moteur d'inférence statistique dont la fonction est d'inférer les causes probables des entrées sensorielles" (3). le neurone binaire stochastique génère une probabilité que son état soit 0 ou 1. L'entrée de données n'est normalement pas considérée comme une couche, mais dans le mode de génération de la machine Helmholtz, la couche de données reçoit l'entrée de la couche intermédiaire a des poids séparés à cet effet, donc il est considéré comme une couche. Ce réseau comporte donc 3 couches.

Autoencodeur

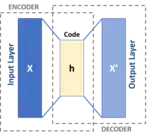
Un réseau feed-forward qui vise à trouver une bonne représentation de la couche intermédiaire de son monde d'entrée. Ce réseau est déterministe, il n'est donc pas aussi robuste que son successeur le VAE.

Auto-encodeur variationnel

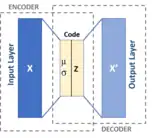
Applique l'inférence variationnelle à l'autoencodeur. La couche intermédiaire est un ensemble de moyennes et de variances pour les distributions gaussiennes. La nature stochastique permet une imagination plus robuste que l'auto-encodeur déterministe.

Celles-ci sont inspirées des machines de Helmholtz[18] et combinent un réseau de probabilité avec des réseaux de neurones. Un Autoencoder est un réseau CAM à 3 couches, où la couche intermédiaire est censée être une représentation interne des modèles d'entrée. Le réseau neuronal du codeur est une distribution de probabilité ${\displaystyle q_{\varphi }}$(z étant donné x) et le réseau du décodeur est ${\displaystyle p_{\theta }}$(x étant donné z). Les poids sont nommés ${\displaystyle \varphi }$ et ${\displaystyle \theta }$ plutôt que W et V comme dans Helmholtz - une différence cosmétique. Ces 2 réseaux ici peuvent être entièrement connectés ou utiliser un autre schéma NN.

Ce tableau présente des schémas de connexion de différents réseaux non supervisés.

Parmi les réseaux portant des noms de personnes, seul Hopfield travaillait directement avec les réseaux de neurones. Boltzmann et Helmholtz ont précédé les réseaux de neurones artificiels, mais leurs travaux en physique et physiologie ont inspiré les méthodes analytiques utilisées.

L'exemple classique d'apprentissage non supervisé dans l'étude des réseaux de neurones est le principe de Donald Hebb, c'est-à-dire que les neurones qui s'activent ensemble se connectent ensemble[20]. La règle de Hebb stipule que la connexion est renforcée indépendamment d'une erreur, mais est exclusivement en fonction de la coïncidence des potentiels d'action entre les deux neurones[21] - [22]. Une version similaire qui modifie les poids synaptiques prend en compte le temps entre les potentiels d'action (plasticité dépendante du moment du pic ou STDP). L'apprentissage hebbien a été supposé sous-tendre une gamme de fonctions cognitives, telles que la reconnaissance de formes et l'apprentissage expérientiel.

Parmi les modèles de réseau de neurones, la carte autoadaptative (SOM) et la théorie de la résonance adaptative (ART) sont couramment utilisées dans les algorithmes d'apprentissage non supervisé. Le SOM est une organisation topographique dans laquelle les emplacements proches sur la carte représentent des entrées avec des propriétés similaires. Le modèle ART permet au nombre de clusters de varier en fonction de la taille du problème et permet à l'utilisateur de contrôler le degré de similitude entre les membres des mêmes clusters au moyen d'une constante définie par l'utilisateur appelée paramètre de vigilance. Les réseaux ART sont utilisés pour de nombreuses tâches de reconnaissance de formes, telles que la reconnaissance automatique de cibles et le traitement des signaux sismiques[22].