Carte autoadaptative
Les cartes autoadaptatives, cartes auto-organisatrices ou cartes topologiques forment une classe de réseau de neurones artificiels fondée sur des méthodes d'apprentissage non supervisées.
Elles sont souvent désignées par le terme anglais self organizing maps (SOM), ou encore cartes de Kohonen du nom du statisticien ayant développé le concept en 1984. La littérature utilise aussi les dénominations : « réseau de Kohonen », « réseau autoadaptatif » ou « réseau autoorganisé ».
Elles sont utilisées pour cartographier un espace réel, c'est-à-dire pour étudier la répartition de données dans un espace à grande dimension. En pratique, cette cartographie peut servir à réaliser des tâches de discrétisation, quantification vectorielle ou classification.
Idée de base
Ces structures intelligentes de représentation de données sont inspirées, comme beaucoup d’autres créations de l’intelligence artificielle, par la biologie. Il s'agit de reproduire le principe neuronal du cerveau des vertébrés : des stimuli de même nature excitent une région du cerveau bien particulière. Les neurones sont organisés dans le cortex de façon à interpréter tous les types de stimuli imaginables. De la même manière, la carte autoadaptative se déploie de façon à représenter un ensemble des données, et chaque neurone se spécialise pour représenter un groupe bien particulier des données selon les points communs qui les rassemblent. Elle permet une visualisation en dimension multiple de données croisées.
Techniquement, la carte réalise une « quantification vectorielle » de l'espace de données. Cela signifie « discrétiser l'espace » ; c'est-à-dire le diviser en zones, et affecter à chaque zone un point significatif dit « vecteur référent ».
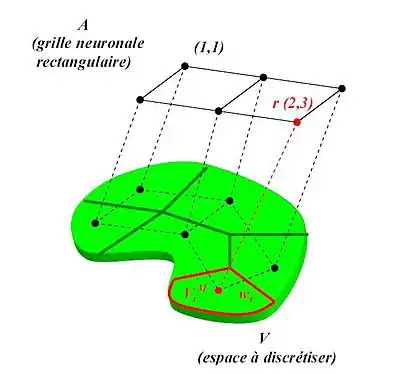
Architecture
D'un point de vue architectural, les cartes auto-organisatrices de Kohonen sont constituées d'une grille (le plus souvent uni- ou bidimensionnelle). Dans chaque nœud de la grille se trouve un « neurone ». Chaque neurone est lié à un vecteur référent, responsable d'une zone dans l'espace des données (appelé encore espace d'entrée).
Dans une carte auto-organisatrice, les vecteurs référents fournissent une représentation discrète de l'espace d'entrée. Ils sont positionnés de telle façon qu'ils conservent la forme topologique de l'espace d'entrée. En gardant les relations de voisinage dans la grille, ils permettent une indexation facile (via les coordonnées dans la grille). Ceci s'avère utile dans divers domaines, comme la classification de textures, l'interpolation entre des données, la visualisation des données multidimensionnelles.
Soit A la grille neuronale rectangulaire d'une carte auto-organisatrice. Une carte de neurones affecte à chaque vecteur d'entrée un neurone désigné par son vecteur de position , tel que le vecteur référent soit le plus proche de v.
Mathématiquement, on exprime cette association par une fonction :
Cette fonction permet de définir les applications de la carte.
- quantificateur vectoriel : on approxime chaque point dans l'espace d'entrée par le vecteur référent le plus proche par :
- classificateur en utilisant la fonction
on affecte à chaque neurone de la grille une étiquette correspondant à une classe ; tous les points de l'espace d'entrée qui se projettent sur un même neurone appartiennent à la même classe. Une même classe peut être associée à plusieurs neurones.
Algorithme d'apprentissage
Principe
Après une initialisation aléatoire des valeurs de chaque neurone, on soumet une à une les données de l'espace d'entrée à la carte autoadaptative. Selon les valeurs des neurones, il y en a un, appelé neurone gagnant, qui répond le mieux au stimulus ; c'est celui dont la valeur est la plus proche de la donnée présentée. Ce neurone est alors gratifié d'un changement de valeur pour qu'il réponde encore mieux à un autre stimulus de même nature que le précédent. Par là-même, on gratifie un peu aussi les neurones voisins du gagnant avec un facteur multiplicatif du gain inférieur à un. Ainsi, c'est toute la région de la carte autour du neurone gagnant qui se spécialise. En fin d'algorithme, lorsque les neurones ne bougent plus, ou seulement très peu, à chaque itération, la carte auto-organisatrice recouvre toute la topologie des données.
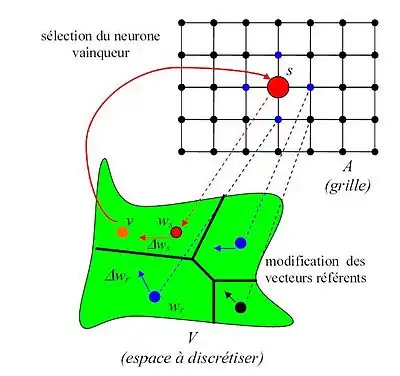
Formalisation mathématique
La cartographie de l'espace d'entrée est réalisée en adaptant les vecteurs référents . L'adaptation est faite par un algorithme d'apprentissage dont la puissance réside dans la compétition entre neurones et dans l'importance donnée à la notion de voisinage.
Une séquence aléatoire de vecteurs d'entrée est présentée pendant l'apprentissage. Avec chaque vecteur, un nouveau cycle d'adaptation est démarré. Pour chaque vecteur v dans la séquence, on détermine le neurone vainqueur, c'est-à-dire le neurone dont le vecteur référent approche v le mieux possible :
Le neurone vainqueur s et ses voisins (définis par une fonction d'appartenance au voisinage) déplacent leurs vecteurs référents vers le vecteur d'entrée
avec
où représente le coefficient d'apprentissage et la fonction qui définit l'appartenance au voisinage.
Le coefficient d'apprentissage définit l'amplitude du déplacement global de la carte.
Sur la notion de voisinage
Tout comme dans le cortex, les neurones sont reliés les uns aux autres, c'est la topologie de la carte. La forme de la carte définit les voisinages des neurones et donc les liaisons entre neurones.
La fonction de voisinage décrit comment les neurones dans la proximité du vainqueur s sont entraînés dans le mouvement de correction. On utilise en général :
où s'appelle coefficient de voisinage. Son rôle est de déterminer un rayon de voisinage autour du neurone vainqueur.
La fonction de voisinage h force les neurones qui se trouvent dans le voisinage de s à rapprocher leurs vecteurs référents du vecteur d'entrée v. Moins un neurone est proche du vainqueur dans la grille, moins son déplacement est important.
La correction de vecteurs référents est pondérée par les distances dans la grille. Cela fait apparaître, dans l'espace d'entrée, les relations d'ordre dans la grille.
Pendant l'apprentissage la carte décrite par les vecteurs référents du réseau évolue d'un état aléatoire vers un état de stabilité dans lequel elle décrit la topologie de l'espace d'entrée tout en respectant les relations d'ordre dans la grille.
Propriétés
- Similitude des densités dans l'espace d'entrée : la carte reflète la distribution des points dans l'espace d'entrée. Les zones dans lesquelles les vecteurs d'entraînement v sont tirés avec une grande probabilité d'occurrence sont cartographiées avec une meilleure résolution que les zones dans lesquelles les vecteurs d'entraînement v sont tirés avec une petite probabilité d'occurrence.
- Préservation des relations topologiques : des neurones voisins dans la grille occupent des positions voisines dans l'espace d'entrée (préservation des voisinages de la grille) ; et des points proches dans l'espace d'entrée se projettent sur des neurones voisins dans la grille (préservation de la topologie de l'espace d'entrée). Les neurones ont tendance à discrétiser l'espace de façon ordonnée.
Avantages et inconvénients des cartes autoadaptatives
Les ancêtres des cartes auto-organisatrices, les algorithmes comme « k-moyennes », réalisent la discrétisation de l'espace d'entrée en ne modifiant à chaque cycle d'adaptation qu'un seul vecteur référent. Leur processus d'apprentissage est donc très long.
L'algorithme de Kohonen profite des relations de voisinage dans la grille pour réaliser une discrétisation dans un temps très court. On suppose que l'espace n'est pas constitué de zones isolées, mais de sous-ensembles compacts. Donc en déplaçant un vecteur référent vers une zone, on peut se dire qu'il y a probablement d'autres zones dans la même direction qui doivent être représentées par des vecteurs référents. Cela justifie le fait de déplacer les neurones proches du vainqueur dans la grille dans cette même direction, avec une amplitude de déplacement moins importante. L'algorithme comporte des opérations simples ; il présente donc l'avantage d'un faible de coût de calculs.
Le voisinage dans les cartes autoadaptatives est malheureusement fixe, et une liaison entre neurones ne peut être cassée même pour mieux représenter des données discontinues. Les Growing Cell Structure, ou Growing Neural Gas, sont la solution à ce problème. Des neurones et les liaisons entre neurones peuvent y être supprimés ou ajoutés quand le besoin s'en fait sentir.
Notes et références
Voir aussi
Bibliographie
- (en) T. Kohonen, Self-Organized Formation of Topologically Correct Feature Maps, Biological Cybernetics, vol. 46, pp. 59–69, 1982.
- (en) T. Kohonen, Self-Organizing Maps, vol. 30, Springer Verlag, 1995.
- (en) H. J. Ritter, T. M. Martinetz, et K. J. Schulten, Neural Computation and Self-Organizing Maps : An Introduction, Addison–Wesley, 1992.
















