Théorie des écoulements à potentiel de vitesse
En mécanique des fluides, la théorie des écoulements à potentiel de vitesse est une théorie des écoulements de fluide où la viscosité est négligée. Elle est très employée en hydrodynamique.
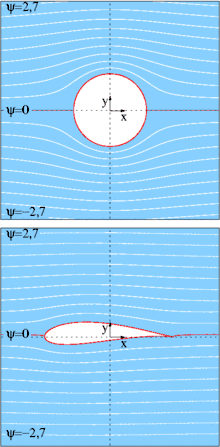
La théorie se propose de résoudre les équations de Navier-Stokes dans les conditions suivantes :
- l'écoulement est stationnaire
- le fluide n'est pas visqueux
- il n'y a pas d'action externe (flux de chaleur, électromagnétisme, gravité ...)
Équations
La formulation différentielle des équations de Navier-Stokes en coordonnées cartésiennes est :
- Équation de continuité (ou équation de bilan de la masse)
- Équation de bilan de la quantité de mouvement
- Équation de bilan de l'énergie
Dans ces équations :
- représente le temps (unité SI : ) ;
- désigne la masse volumique du fluide (unité SI : ) ;
- désigne la vitesse eulérienne d'une particule fluide (unité SI : ) ;
- désigne la pression (unité SI : ) ;
- est le tenseur des contraintes visqueuses (unité SI : ) ;
- désigne la résultante des forces massiques s'exerçant dans le fluide (unité SI : ) ;
- est l'énergie totale par unité de masse (unité SI : ) ;
- est le flux de chaleur perdu par conduction thermique (unité SI : ) ;
- représente la perte de chaleur volumique due au rayonnement (unité SI : ).
Fluide incompressible
Aux équations précédentes, il faut rajouter les conditions de notre cas soit :
- le fluide est incompressible
- le fluide est stationnaire soit
- , ,
- le fluide n'est pas visqueux
- ,
- il n'y a pas d'action externe (flux de chaleur, électromagnétisme, gravité ...)
- , , ...
d'où les équations se simplifient fortement :
Avec les conditions aux limites, le système d'équations est solvable. La première équation est indépendante des deux autres, il suffit de trouver une solution à cette équation pour ensuite déterminer les deux autres.
Comme est constant, alors l'équation est : .
Donc il existe une fonction telle que :
où est le vecteur vitesse du fluide en un point de l'espace des équations de Navier-Stokes.
L'équation prend la forme suivante :
soit
sans oublier les conditions aux limites.
Soit, sous une autre notation : .
Solution
La solution de l’équation avec ses conditions aux limites a été donnée par George Green et s’écrit :
avec :
- S une surface qui est le bord du domaine dans lequel est plongé le profil (aile d'avion, voile de bateau...). Le domaine doit être suffisamment grand pour que le fluide se perturbe « tranquillement » autour du profil sans qu'apparaissent des effets de bord notables. Un domaine de trois à quatre fois la dimension du profil est un minimum.
- M(x,y,z) un point à l’intérieur du volume limité par une surface fermée S (qui peut s’étendre à l’infini) ;
- et étant nuls à l’extérieur de la surface S ;
- le vecteur unitaire normal à S orienté vers l’intérieur ;
- r = PM le vecteur joignant un point courant P de la surface S au point M ou on exprime le potentiel .
Résolution
Sauf pour des formes simples de profil, la résolution de l'équation est uniquement numérique. Du fait même que l'écoulement est considéré comme stationnaire, les résultats de calcul ne sont pas turbulents. Donc ce modèle n'est réaliste qu'à faible incidence. À forte incidence, la théorie diverge fortement de la réalité où le profil génère beaucoup de turbulences.
Fluide compressible
Cas général
De même cette théorie peut être étendue à un modèle irrotationnel compressible[1].
avec nombre de Mach
- et
où a est la vitesse locale du son. est le vecteur vitesse du fluide et est égal à : . L'équation est valide pour des vitesses sub-, trans- et supersonique et pour une incidence arbitraire tant que le flux reste irrotationnel [1].
Dans le cas subsonique ou supersonique mais pas transsonique ou hypersonique, à faible incidence et un profil mince, nous pouvons diviser la vitesse en deux parties : la vitesse non perturbée V∞ dans la direction x, et le reste dans ∇φ soit :
Pour des petites perturbations en appliquant la théorie des Théories des perturbations [1] une linéarisation pour des petites perturbations est faite. Les équations se simplifient et deviennent [1]:
avec M∞ = V∞ / a∞ le nombre de Mach du flux entrant non perturbé. Ces équations linéaires sont beaucoup plus simples à résoudre que les équations initiales.
Acoustique
Aux équations de base, il faut rajouter les conditions suivantes :
- le fluide est stationnaire soit
- , ,
- le fluide n'est pas visqueux
- ,
- il n'y a pas d'action externe (flux de chaleur, électromagnétisme, gravité ...)
- , , ...
d'où les équations se simplifient fortement :
La densité est décomposée comme suit avec la densité à l'équilibre définie comme suit .
On note :
En utilisant massivement les théorèmes de l'analyse vectorielle, il est obtenu :
La vitesse est décomposée comme suit avec la vitesse moyenne définie comme suit .
En procédant de façon similaire en se concentrant uniquement sur , en négligeant les phénomènes du deuxième ordre (appelé approximation de l'acoustique) et en considérant les variations de pression comme purement adiabatiques, nous arrivons à modéliser les ondes acoustiques comme suit :
avec la vitesse v' = ∇φ et la moyenne de la vitesse du son dans un matériau homogène. est définie comme suit : avec le coefficient de compressibilité adiabatique ().
Attention la vitesse v est vue au sens eulérien, c'est pas la vitesse d'une particule déterminée mais la vitesse des particules passant par un point précis de l'espace.
Voir aussi
Article connexe
Liens externes
- Théorie générale des écoulements à potentiel de vitesse sur air-et-terre.info
- (en) Potential flow theory par A. H. Techet, du MIT
- (en) Potential flow theory par Nuno Fonseca, de l'Instituto Superior Técnico
- (en) Chanson Hubert, Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows http://espace.library.uq.edu.au/view/UQ:191112, Boca Raton, CRC Press, Taylor & Francis Group, , relié (ISBN 978-0-415-49271-3, LCCN 2008051277)
Références
- J.D. Anderson, Modern compressible flow, McGraw-Hill, (ISBN 0-07-242443-5), pp. 358–359.


![{\displaystyle {\frac {\partial \left(\rho e\right)}{\partial t}}+\operatorname {div} \left[\;\left(\rho e+p\right){\vec {v}}\;\right]=\operatorname {div} \left({\overline {\overline {\tau }}}\cdot {\vec {v}}\right)+\rho {\vec {f}}\cdot {\vec {v}}-\operatorname {div} ({\vec {\dot {q}}})+r}](https://img.franco.wiki/i/310483970be21b9385094fbe6ba4b60013ae150d.svg)


























![{\displaystyle \operatorname {div} \left[\;\left(\rho e+p\right){\vec {v}}\;\right]=0}](https://img.franco.wiki/i/4b89c5a592f0b2cdb90a46db097da74381a2b144.svg)




















![{\displaystyle {\frac {\partial \left(\rho e\right)}{\partial t}}+\operatorname {div} \left[\;\left(\rho e+p\right){\vec {v}}\;\right]=0}](https://img.franco.wiki/i/12944eb712995b30bc9e33c1a482de6fdfd7fc67.svg)














