Théorème de Lambek-Moser

Les quatre fonctions ${\displaystyle f}$, ${\displaystyle f^{*}}$, ${\displaystyle F}$, et ${\displaystyle F^{*}}$, correspondant aux deux suites de Beatty 1, 3, 4, 6, ... et 2, 5, 7, 10, ... , suites des arrondis des multiples de ${\displaystyle \varphi }$ et de ${\displaystyle \varphi +1}$, où ${\displaystyle \varphi }$ est le nombre d'or.

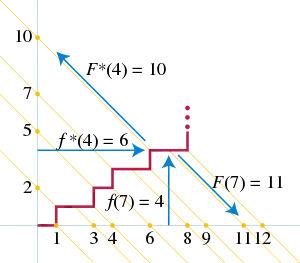
Soit ${\displaystyle f}$ une fonction allant des entiers naturels non nuls vers les entiers (nuls ou non) croissante (chaque valeur de la suite ${\displaystyle f(1),f(2),f(3),\dots }$ est égale ou supérieure à la précédente) et non bornée. Une telle fonction n'a en général pas d'inverse, puisqu'elle peut sauter des valeurs ; on va définir une fonction ${\displaystyle f^{*}}$ elle aussi croissante et non bornée, aussi proche que possible d'un inverse de ${\displaystyle f}$ au sens où, pour tout entier ${\displaystyle n}$,

$${\displaystyle f{\bigl (}f^{*}(n){\bigr )}<n\leq f{\bigl (}f^{*}(n)+1{\bigr )}.}$$

Cela revient à définir ${\displaystyle f^{*}(n)}$ comme le nombre d'entiers ${\displaystyle m}$ pour lesquels ${\displaystyle f(x)<n}$ ; il en résulte que ${\displaystyle f^{*}{}^{*}=f}$[2]. Les représentations de ${\displaystyle f}$ et ${\displaystyle f^{*}}$ comme des histogrammes sont symétriques l'une de l'autre par rapport à la première bissectrice ${\displaystyle x=y}$[3].

À partir de ${\displaystyle f}$ et ${\displaystyle f^{*}}$, on définit deux nouvelles fonctions ${\displaystyle F}$ et ${\displaystyle F^{*}}$ par :

$${\displaystyle {\begin{aligned}F(n)&=f(n)+n\\F^{*}(n)&=f^{*}(n)+n\\\end{aligned}}}$$

La première partie du théorème de Lambek–Moser affirme que chaque entier non nul est atteint une fois et une seule, soit par ${\displaystyle F}$, soit par ${\displaystyle F^{*}}$. Autrement dit, les valeurs prises par ${\displaystyle F}$ et celles prises par ${\displaystyle F^{*}}$ forment deux sous-ensembles complémentaires d'entiers non nuls. Plus précisément, chacune de ces deux fonctions envoie ${\displaystyle n}$ sur le ${\displaystyle n}$-ème élément du sous-ensemble correspondant[2].

Comme exemple de cette construction, soit ${\displaystyle f(n)=n^{2}}$. Son inverse dans ${\displaystyle \mathbb {R} }$ est la fonction racine carrée, dont l'approximation dans les entiers (au sens du théorème de Lambek–Moser) est ${\displaystyle f^{*}(n)=\lfloor {\sqrt {n-1}}\rfloor }$ (le plus grand entier inférieur ou égal à ${\displaystyle {\sqrt {n-1}}}$). On a donc ${\displaystyle F(n)=n^{2}+n}$ et ${\displaystyle F^{*}(n)=\lfloor {\sqrt {n-1}}\rfloor +n.}$ Pour ${\displaystyle n=1,2,3,\dots }$, les valeurs de ${\displaystyle F}$ sont les nombres oblongs

2, 6, 12, 20, 30, 42, 56, 72, 90, 110, ...

tandis que celles de ${\displaystyle F^{*}}$ sont

1, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, ....

ces deux suites forment une partition de ${\displaystyle \mathbb {N} ^{*}}$ : chaque entier (non nul) appartient à une et une seule des deux[3]. Le théorème de Lambek–Moser affirme que ce phénomène se produit pour tout choix de ${\displaystyle f}$ ayant les propriétés voulues[2].

Les deux fonctions ${\displaystyle f}$ (flèches bleues vers la droite) et ${\displaystyle f^{*}}$ (flèches rouges) correspondant à la partition des entiers en nombres premiers (2, 3, 5, 7, ...) et non-premiers (1, 4, 6, 8, ...) ; cette visualisation se base sur une méthode due à Angel[4].

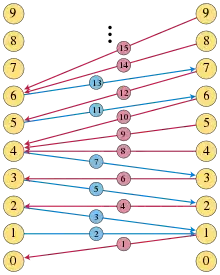
La seconde partie du théorème de Lambek–Moser affirme la réciproque : toute partition des entiers provient de cette construction. Plus précisément, si ${\displaystyle S=s_{1},s_{2},\dots }$ et ${\displaystyle S^{*}=s_{1}^{*},s_{2}^{*},\dots }$ sont deux suites croissantes d'entiers complémentaires, il existe deux fonctions ${\displaystyle f}$ et ${\displaystyle f^{*}}$ produisant ces suites par la construction précédente : il suffit de définir ${\displaystyle f(n)=s_{n}-n}$ et ${\displaystyle f^{*}(n)=s_{n}^{*}-n}$[2].

Par exemple, pour la partition en nombres pairs et impairs, les fonctions ${\displaystyle F(n)}$ et ${\displaystyle F^{*}(n)}$ donnant respectivement le ${\displaystyle n}$-ème nombre pair ou impair, on obtient${\displaystyle f(n)=F(n)-n=n}$ et ${\displaystyle f^{*}(n)=F^{*}(n)-n=n-1}$ , formant un couple d’inverses au sens précédent. La partition correspondant à la parité du nombre de 1 en représentation binaire (les nombres odieux (en) et les autres) utilise presque les mêmes fonctions, ajustées par les valeurs de la suite de Thue–Morse[5].

Lambek et Moser ont donné une construction directe de ${\displaystyle F^{*}}$ en partant de ${\displaystyle F^{\#}(n)}$ , la fonction donnant le nombre de valeurs de ${\displaystyle x}$ pour lesquelles ${\displaystyle F(m)\leq n}$; on a alors, pour tout ${\displaystyle n}$, ${\displaystyle F^{*}(n)}$ donné par la limite de la suite

$${\displaystyle n,n+F^{\#}(n),n+F^{\#}{\bigl (}n+F^{\#}(n){\bigr )},\dots ,}$$

(laquelle devient donc constante à partir d’un certain rang)[6].

Lambek et Moser prennent les nombres premiers comme exemple, prolongeant un travail antérieur de Viggo Brun et Derrick Lehmer[7]. Si ${\displaystyle \pi (n)}$ est la fonction de compte des nombres premiers, alors le ${\displaystyle n}$-ème nombre composé (en comptant 1 comme composé) est donné par la limite de la suite[6]

$${\displaystyle n,n+\pi (n),n+\pi {\bigl (}n+\pi (n){\bigr )},\dots }$$

Pour certaines suites d'entiers, l'expression précédente devient constante après un nombre fixé d'étapes, permettant une formule explicite. Ainsi, le ${\displaystyle n}$-ème entier qui n'est pas une puissance ${\displaystyle k}$-ème est donné par la formule ${\displaystyle n+\left\lfloor {\sqrt[{k}]{n+\lfloor {\sqrt[{k}]{n}}\rfloor }}\right\rfloor }$[8].

Le théorème fut découvert par Leo Moser et Joachim Lambek, qui le publièrent en 1954. Moser et Lambek disent avoir été inspirés par le travail antérieur de Samuel Beatty sur les suites portant son nom, ainsi que par celui de Viggo Brun et Derrick Lehmer[7] au début des années 1930. Edsger Dijkstra a donné une preuve visuelle du résultat[9], ainsi qu'une preuve basée sur un raisonnement algorithmique[10].

• Suite de Hofstadter (la suite Figure-Figure est un exemple d'application du théorème)

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Lambek–Moser theorem » (voir la liste des auteurs).