Théorème de Jung

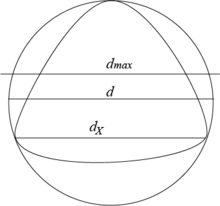
Toute partie bornée non vide X de l'espace euclidien de dimension n est incluse dans une unique boule fermée de rayon minimal, et le diamètre d de cette boule est relié au diamètre ${\displaystyle d_{X}=\sup _{M,N\in X}MN}$ de la partie X par les inégalités :

${\displaystyle d_{X}\leqslant d\leqslant d_{max}=d_{X}{\sqrt {\frac {2n}{(n+1)}}}.}$

Le cas d'égalité dans l'inégalité de droite est atteint par le simplexe régulier de dimension n.

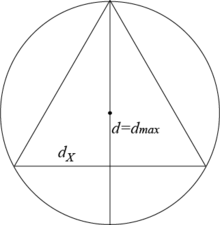
Le cas le plus commun du théorème de Jung est celui du plan euclidien avec n = 2. Dans ce cas, le théorème assure qu'il existe un cercle entourant tous les points dont le diamètre satisfait

${\displaystyle d\leqslant {\frac {2}{\sqrt {3}}}d_{X}<1,155.d_{X}}$

Le cas d'égalité est obtenu pour un triangle équilatéral.

Existence d'une boule de rayon minimum : l'application qui, à tout point M, associe la borne supérieure des distances de M aux points de X, est continue (car 1-lipschitzienne) et tend vers +∞ quand M s'éloigne à l'infini, donc elle atteint son minimum r, en un point C, centre d'une telle boule de diamètre ${\displaystyle d=2r}$.

Unicité de C : se déduit du théorème de la médiane.

Majoration : d'après le théorème de Helly, il suffit de la démontrer dans le cas où X est fini et de cardinal inférieur ou égal à n + 1. Notons alors ${\displaystyle M_{0},_{\cdots },M_{m}}$ (${\displaystyle m\leqslant n}$) les points de X dont la distance au centre C vaut exactement r. On se convainc rapidement par un argument variationnel que C appartient à leur enveloppe convexe. Il existe donc des réels

${\displaystyle \lambda _{0},\ldots ,\lambda _{m}\geqslant 0{\text{ tels que }}\sum \lambda _{i}=1{\text{ et }}C=\sum \lambda _{i}M_{i}.}$

Pour chaque indice k de 0 à m on a alors :

${\displaystyle (1-\lambda _{k})d_{X}^{2}=\sum _{i\neq k}\lambda _{i}d_{X}^{2}\geqslant \sum _{i\neq k}\lambda _{i}(M_{k}M_{i})^{2}=\sum _{i=0}^{m}\lambda _{i}{\overrightarrow {M_{k}M_{i}}}^{2}=\sum _{i=0}^{m}\lambda _{i}(2r^{2}-2{\overrightarrow {CM_{k}}}\cdot {\overrightarrow {CM_{i}}})=2r^{2}=d^{2}/2}$

d'où, en sommant :

${\displaystyle md_{X}^{2}\geqslant (m+1)d^{2}/2{\text{ donc }}{\frac {d_{X}^{2}}{d^{2}}}\geqslant 2\left(1+{\frac {1}{m}}\right)\geqslant 2\left(1+{\frac {1}{m}}\right),}$

ce qui conclut.

Le simplexe régulier de dimension n a pour diamètre la longueur a de ses côtés. Sa sphère circonscrite a pour diamètre ${\displaystyle a{\sqrt {\frac {2n}{(n+1)}}}}$ qui est aussi le diamètre de sa boule englobante minimale, d'où l'égalité dans l'inégalité.

• (en) Mikhail Katz (en), « Jung's theorem in complex projective geometry », Q. J. Math., vol. 36, n^o 4,‎ 1985, p. 451-466 (DOI 10.1093/qmath/36.4.451)
• (en) B. V. Dekster, « The Jung theorem for the spherical and hyperbolic spaces », Acta Math. Sci. Hungar., vol. 67, n^o 4,‎ 1995, p. 315-331 (DOI 10.1007/BF01874495)
• (en) B. V. Dekster, « The Jung theorem in metric spaces of curvature bounded above », Proc. Amer. Math. Soc., vol. 125, n^o 8,‎ 1997, p. 2425-2433 (DOI 10.1090/S0002-9939-97-03842-2)
• (de) Heinrich Jung, « Über die kleinste Kugel, die eine räumliche Figur einschliesst », J. reine angew. Math., vol. 123,‎ 1901, p. 241-257 (lire en ligne)
• (de) Heinrich Jung, « Über den kleinsten Kreis, der eine ebene Figur einschließt », J. reine angew. Math., vol. 137,‎ 1910, p. 310-313 (lire en ligne)
• (en) Hans Rademacher et Otto Toeplitz, The Enjoyment of Mathematics : Selections from Mathematics for the Amateur, Dover, 1990, 205 p. (ISBN 978-0-486-26242-0, lire en ligne), chap. 16 (pour une partie finie du plan)
• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Jung's theorem » (voir la liste des auteurs).

• Le théorème de Blashke qui affirme que dans un convexe du plan de plus petite largeur ${\displaystyle l}$ le disque de plus grand diamètre inclus a un diamètre ${\displaystyle \geqslant 2l/3}$.
• Sphère englobante
• Disque minimum
• Problème du recouvrement universel de Lebesgue