Théorème de Blaschke-Lebesgue

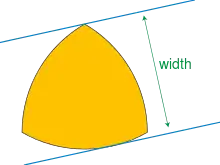
La largeur dans une direction donnée d'un convexe ${\displaystyle K}$ du plan euclidien est définie comme la distance minimale entre deux droites parallèles dans cette direction qui l'englobent. Ces deux droites sont toutes deux nécessairement des tangentes à ${\displaystyle K}$. Une courbe de largeur constante est la frontière d'un convexe pour lequel la distance définie précédemment ne dépend pas de la direction choisie. Ces courbes comprennent à la fois le cercle et le triangle de Reuleaux, un triangle incurvé formé de trois arcs de cercle de même rayon centrés à un point d'intersection des deux autres cercles. L'aire englobée par un triangle de Reuleaux de largeur ${\displaystyle l}$ est égale à

${\displaystyle {\frac {1}{2}}(\pi -{\sqrt {3}})l^{2}\approx 0,70477.l^{2}}$ , voir la suite A060708 de l'OEIS.

Le théorème de Blaschke – Lebesgue stipule que tout convexe de largeur constante ${\displaystyle l}$ a une aire supérieure ou égale à cette valeur, avec égalité si et seulement si le convexe est délimité par un triangle de Reuleaux[1].

Parmi tous les convexes du plan de plus petite largeur ${\displaystyle l}$, c'est le triangle équilatéral de hauteur ${\displaystyle l}$ (qui est aussi sa plus petite largeur) qui a la plus petite aire : ${\displaystyle {\frac {\sqrt {3}}{3}}l^{2}\approx 0,58.l^{2}}$, mais ce n’est pas un convexe de largeur constante[2].

Le théorème de Blaschke-Lebesgue a été publié indépendamment en 1914 par Henri Lebesgue[3] et en 1915 par Wilhelm Blaschke[4]. Depuis leurs travaux, plusieurs autres preuves ont été publiées[2].

Le théorème est également valable dans le plan hyperbolique[5].

Pour toute distance définie dans le plan à partir d'une norme, un théorème analogue est vérifié, en définissant les cercles du triangle de Reuleaux à partir de cette distance[6].

Le théorème de Blaschke-Lebesgue a été utilisé pour fournir une stratégie efficace pour une généralisation du jeu de Bataille navale, dans laquelle un joueur a un navire convexe et l'autre joueur, après avoir trouvé un point de ce navire, cherche à déterminer sa position en minimisant le nombre de tirs ratés. Pour un navire avec ${\displaystyle n}$ points de la grille, il est possible de borner le nombre de coups ratés par ${\displaystyle O(\log \log n)}$ .

Par l'inégalité isopérimétrique, les courbes de largeur constante donnée dans le plan euclidien de plus grande aire sont les cercles[1]. Le périmètre d'une courbe de largeur constante ${\displaystyle l}$ est ${\displaystyle \pi l}$, quelle que soit sa forme ; c'est le théorème de Barbier.

On ne connaît pas les surfaces de largeur constante de l'espace tridimensionnel ayant le volume minimal. Bonnesen et Fenchel ont conjecturé en 1934 que ces surfaces sont les deux corps de Meissner obtenus en arrondissant certaines des arêtes d'un tétraèdre de Reuleaux , mais cela reste à prouver.

Tout convexe de plus petite largeur ${\displaystyle l}$ contient un disque de largeur ${\displaystyle 2l/3}$. On ne peut améliorer la valeur 2/3 car le disque inscrit dans un triangle équilatéral de hauteur ${\displaystyle l}$ (qui est aussi sa plus petite largeur) est de rayon ${\displaystyle 2l/3}$[7].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Blaschke–Lebesgue theorem » (voir la liste des auteurs).