Problème du recouvrement universel de Lebesgue

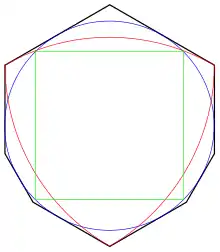
Le théorème de Jung (1901) assure que le disque de rayon ${\displaystyle 1/{\sqrt {3}}}$, d'aire ${\displaystyle \pi /3\approx 1,07}$ a la propriété de recouvrement universel.

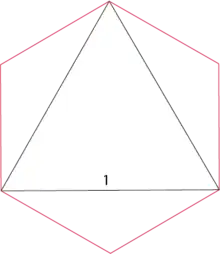
Après avoir montré qu'il suffit qu'un convexe recouvre toutes les courbes de largeur constante 1 pour recouvrir tous les ensembles de diamètre 1, Pál a montré que l'hexagone régulier de cercle inscrit de diamètre 1, donc de rayon ${\displaystyle 1/{\sqrt {3}}}$, et d'aire ${\displaystyle {\sqrt {3}}/2\approx 0,866}$ a la propriété de recouvrement universel.

Puis il a montré qu'on pouvait "raboter" deux sommets de l'hexagone, en enlevant deux triangles laissant toujours un cercle inscrit de diamètre 1, tout en conservant la propriété. Cet hexagone tronqué de Pál a une aire de ${\displaystyle 2-{\frac {2}{\sqrt {3}}}\approx 0,845}$ .

En 1936, Roland Sprague a montré qu'on pouvait retirer un fragment de l'hexagone tronqué de Pál près de l'un des autres sommets, tout en conservant la propriété de recouvrement, ce qui donne une aire ${\displaystyle \leqslant 0,844137708436}$ [3].

En 1992, Hansen a montré qu'on pouvait supprimer deux autres très petites régions de la solution de Sprague, ramenant la limite supérieure de l'aire à ${\displaystyle 0,844137708398}$. La construction de Hansen a été la première demandant d'utiliser les symétries [4].

En 2015, John Baez, Karine Bagdasaryan et Philip Gibbs ont montré que si les triangles évidés dans le recouvrement de Pál sont coupés suivant un autre angle, il est alors possible de réduire l'aire, ce qui a donné une borne supérieure ${\displaystyle \leqslant 0,8441153}$ [5].

En octobre 2018, Philip Gibbs a publié un article sur arXiv utilisant la géométrie niveau lycée et obtenant une nouvelle réduction à 0,8440935944 [6] - [7].

La borne inférieure la plus connue pour l'aire été donnée en 2005 par Peter Brass et Mehrbod Sharifi en utilisant une combinaison de trois formes dans un alignement optimal, montrant que l'aire d'un convexe recouvrant universel devait avoir une aire ${\displaystyle \geqslant 0,832}$ [8].

• Le problème du ver de Moser, demandant l'aire minimale d'une forme pouvant recouvrir toute courbe de longueur 1.
• Le problème du sofa, demandant de trouver une forme d'aire maximale pouvant passer dans un couloir en forme de L.
• Le problème de l'aiguille de Kakeya, demandant une forme d'aire minimale pouvant recouvrir tout segment de longueur 1 (avec autorisation des translations, mais pas des rotations d'angle non nul).
• Le théorème de sélection de Blaschke, qui peut être utilisé pour prouver que le problème du recouvrement universel de Lebesgue possède une solution.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Lebesgue's universal covering problem » (voir la liste des auteurs).