Problème du sofa

Le problème du sofa est un problème mathématique conceptuel formalisé par le mathématicien Leo Moser en 1966[1]. Il s'agit de trouver le sofa d'aire maximale que l'on peut déplacer horizontalement dans un couloir d'un mètre de large avec un angle droit.

Le sofa de Hammersley n'a pas l'aire maximale connue.

Le sofa de Gerver avec 18 sections de courbes.

Problème qui n'est pas encore résolu, il a déjà été débattu plusieurs fois de façon informelle auparavant[2].

Limites inférieure et supérieure

Les travaux menés rapportent que l’aire maximale, notée $A$ (et souvent appelée constante du canapé) peut pas être inférieure ou supérieure à certaines valeurs (bornes inférieures et bornes supérieures).

Limite inférieure

Une borne inférieure vaut $A\geq \pi /2\approx 1,57079$ . Cela vient du fait qu'un sofa ayant la forme d'un demi-disque de rayon 1, peut tourner dans le coin.

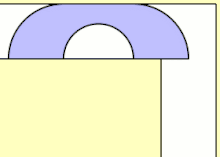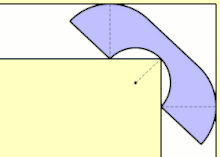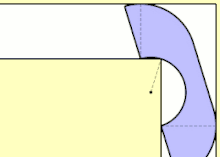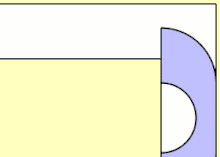
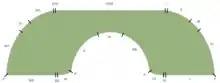
John Hammersley a trouvé une limite inférieure de $A\geq \pi /2+2/\pi \approx 2.2074$ basé sur la forme ressemblant à un téléphone (voir l'animation ci-dessus), composé de deux quarts de rayon 1 de chaque côté d'un rectangle de 1 par $4/\pi$ à partir duquel un demi-disque de rayon $2/\pi$ a été retiré[3] - [4].

Joseph Gerver a trouvé un canapé décrit par 18 sections de courbes, chacune prenant une forme analytique lisse. Cela a augmenté la limite inférieure pour la constante du sofa à environ 2,2195[5] - [6].

Limite supérieure

Hammersley a également trouvé une limite supérieure, montrant que le sofa occupe au plus $2{\sqrt {2}}\approx 2{,}8284$ unités[2] - [7].

Yoav Kallus et Dan Romik ont démontré en juin 2017 que le sofa ne pouvait pas occuper plus de $2{,}37$ unités[8].

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Moving sofa problem » (voir la liste des auteurs).

(en) Leo Moser, « Moving Furniture Through a Hallway », SIAM Review, vol. 8, n^o 3,‎ 1966, p. 381 (DOI 10.1137/1008074).
(en) Neal R. Wagner, « The Sofa Problem », The American Mathematical Monthly, vol. 83, n^o 3,‎ mars 1976, p. 188–189 (DOI 10.2307/2977022, JSTOR 2977022, lire en ligne).
(en) Hallard T. Croft, Kenneth J. Falconer et Richard K. Guy, Unsolved Problems in Geometry, vol. II, Springer-Verlag, coll. « Problem Books in Mathematics; Unsolved Problems in Intuitive Mathematics », 1994 (ISBN 978-0-387-97506-1, lire en ligne).
(en) Steven Finch, « Moving Sofa Constant », MathSoft (version du 7 janvier 2008 sur Internet Archive).
(en) Joseph L. Gerver, « On Moving a Sofa Around a Corner », Geometriae Dedicata, vol. 42, n^o 3,‎ 1992, p. 267–283 (ISSN 0046-5755, DOI 10.1007/BF02414066)
(en) Eric W. Weisstein, « Moving Sofa Problem », sur MathWorld.
(en) Ian Stewart, Another Fine Math You've Got Me Into..., Mineola, N.Y., Dover Publications, 2004 (1^re éd. 1992), 269 p. (ISBN 0-486-43181-9, lire en ligne), chap. 16 (« Sofa, So Good... »), p. 255–268.
(en) Yoav Kallus et Dan Romik, « Improved upper bounds in the moving sofa problem », Advances in Mathematics, vol. 340,‎ 15 décembre 2018, p. 960–982 (DOI 10.1016/j.aim.2018.10.022, arXiv 1706.06630).

Voir aussi

Liens externes

[PDF] Exposé de Pierre Konen, sur le site de MATh.en.JEANS
[PDF] Le problème avec deux angles, sur le site de MATh.en.JEANS

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.