Tempérament inégal
En musique, un tempérament inégal est un système de division de l'octave à structure non régulière destiné à l'accord des instruments à sons fixes.
Les tempéraments inégaux, dérivés du mésotonique, ont permis d’étendre les possibilités de modulation jusque dans des tonalités éloignées, mais avec des différences marquées de couleurs sonores entre les tonalités, dont tous les compositeurs de l'époque baroque ont su user.
Histoire
Les tempéraments inégaux ont été imaginés en grand nombre au XVIIIe siècle par les théoriciens de la musique avant la généralisation du tempérament égal.
Historiquement, les tempéraments inégaux sont postérieurs aux tempéraments mésotoniques dont ils constituent des variantes améliorées ; contrairement à ceux-ci, ils se fondent sur la priorité donnée à certains intervalles : la consonance d'intervalles couramment utilisés étant privilégiée sur celle d'intervalles peu fréquents.
C'était la marotte des théoriciens du XVIIIe siècle de découvrir le tempérament inégal qui présenterait le meilleur compromis possible entre la justesse des octaves, des quintes et des tierces, la non-limitation de l'emploi des différentes tonalités et des possibilités infinies de transposition et de modulation. La réalité concrète de la musique s'est faite en utilisant ces tempéraments inégaux.
À propos du clavecin et du clavicorde, Carl Philipp Emanuel Bach écrit[1] :
« Les deux sortes d'instruments doivent être bien tempérés : en accordant les quartes et les quintes, avec les tierces majeures et mineures et les accords complets pour preuves, il faut affaiblir un tant soit peu la justesse des quintes, en sorte que l'oreille la perçoive à peine et que les vingt-quatre tons soient tous utilisables. »
Il s'agit bien de rendre les vingt-quatre tons utilisables, et non de leur donner à tous la même couleur, ce que fera le tempérament égal.
Avec les tempéraments du XVIIIe siècle, chaque tonalité avait un « coloris sonore » différencié, associé à des propriétés expressives — dont plusieurs musiciens ou théoriciens, tels que Johann Mattheson, Marc-Antoine Charpentier, Jean-Philippe Rameau et Jean-Jacques Rousseau ont proposé des inventaires — et auxquels les musiciens portaient la plus grande attention[2]. Ces tempéraments inégaux ont mobilisé une imagination et une inventivité considérables et certains d’entre eux sont d’une ingéniosité remarquable. Le « Clavier bien tempéré » (« Das wohltemperierte Klavier ») de J. S. Bach fait la preuve de la praticabilité de ces tempéraments inégaux, par opposition aux tempéraments mésotoniques, pour jouer dans les vingt-quatre tons majeurs et mineurs.
Bradley Lehman, un musicologue américain, pense que Bach a laissé dans les dessins de son manuscrit la structure précise du tempérament qu'il préconise : à base de quintes tempérées au 6e de comma pythagoricien, et quelques autres au 12e[3].
Le principe général
Il consiste à répartir des fractions de commas entre les différentes quintes du cycle, plusieurs objectifs étant poursuivis simultanément :
- améliorer la qualité des tierces ou au moins de certaines d'entre elles ;
- améliorer la quinte du loup ;
- fausser au minimum les quintes ;
- étendre les possibilités de modulation.
Ceci étant posé, la recherche du tempérament inégal idéal s'apparente un peu à une « recette de cuisine », car les possibilités sont infinies et aucun tempérament n'est parfait ou ne peut même se prévaloir d'un avantage certain sur les autres. Il y règne donc une certaine subjectivité, ce qui explique que la question excita les passions des théoriciens, chacun étant persuadé de la supériorité de son système. En fonction des objectifs visés, certains sont néanmoins plus astucieux que d'autres et plus faciles à réaliser dans la pratique sur les instruments.
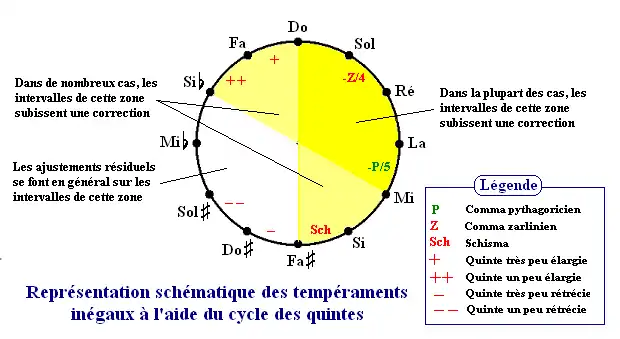
Conventions des schémas
On résume souvent le principe d'un tempérament à l'aide d'un schéma représentant le cycle des quintes, en indiquant pour chacune d'entre elles la correction qui est apportée par rapport à la quinte « juste » pour améliorer les tierces. Ces corrections sont - chez les auteurs les plus rigoureux - exprimées en fractions de comma. On rappelle qu'il faut au total diminuer l'ensemble du cycle d'un comma pythagoricien (pour obtenir une octave pure) et diminuer un groupe de 4 quintes pures consécutives d'un comma syntonique pour obtenir une tierce majeure pure ... en n'oubliant pas que réduire une quinte, c'est en augmenter au moins une autre !
Dans le cas des tempéraments inégaux, les corrections portent plutôt sur les notes des tonalités proches du do majeur. Mais cette règle n'a rien d'absolu.
Exemples commentés de tempéraments inégaux
« Tempérament ordinaire »
Ce tempérament en usage général aux XVIe et XVIIe siècles[4] comprend 3 quintes diminuées (40/27), 8 quintes pythagoriciennes (3/2) et une quinte du loup (192/125). Les quintes diminuées diffèrent donc des quintes pythagoriciennes (pures) d'un comma syntonique ; réparties comme il faut sur le cycle des quintes, elles permettent d'avoir trois tierces majeures pures.
Werckmeister (1691)
Andreas Werckmeister, organiste, expert en facture, compositeur et théoricien des tempéraments est surtout connu aujourd'hui pour avoir décrit plusieurs tempéraments dans son ouvrage de 1691 intitulé Musicalische Temperatur. Les plus connus sont numérotés III, IV et V ; ils sont basés sur une répartition du comma Pythagoricien (c’est-à-dire qu'ils ne comportent aucune tierce pure).
- Werckmeister III
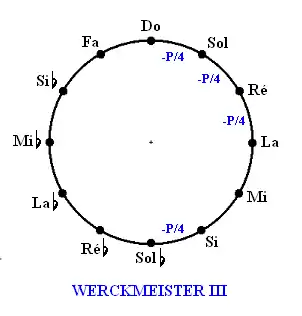
- Le comma pythagoricien est réparti par quarts sur 4 quintes (qui deviennent ainsi un peu courtes) : Do-Sol, Sol-Ré, Ré-La et Si-Sol.
- Ainsi les tierces Do-Mi et Fa-La sont assez proches de la pureté, les autres s'en éloignent progressivement et ce tempérament. Le choix de la quinte tempérée Si-Fa favorise les tonalités en dièses (sol est meilleur que la♭).
- Werckmeister IV
- C'est le plus sophistiqué des tempéraments décrits par Werckmeister car, pour arriver au but qu'il se fixe, il corrige les quintes en plus ou en moins par tiers de comma ditonique.
- Les tierces Si-Ré, Fa-La, Do-Mi, Sol-Si, Ré-Fa et La-Do sont bonnes, corrigées de 2/3 de comma et les deux quintes augmentées d'un tiers de comma sont placées de telle façon qu'aucun véritable loup ne se manifeste.
- Werckmeister V
Chaumont (1695)
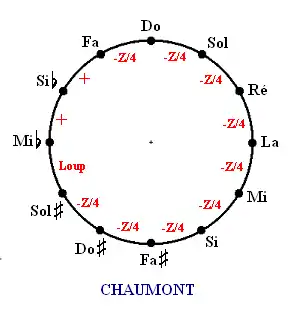
Bien qu'obscur musicien autodidacte (?) de la principauté de Liège, Lambert Chaumont a été après Werckmeister un des premiers à décrire un tempérament inégal qui est une amélioration du tempérament mésotonique à 1/4 de comma.
Il corrige légèrement (en les agrandissant) les quintes mi ![]() -si
-si ![]() et si
et si ![]() -fa ce qui permet de diminuer la fausseté du loup entre sol
-fa ce qui permet de diminuer la fausseté du loup entre sol ![]() et mi
et mi ![]() .
.
Il y a six tierces majeures pures et les autres sont audibles.
Les tierces mi ![]() -sol et si
-sol et si ![]() -ré sont moins mauvaises que les pythagoriciennes.
-ré sont moins mauvaises que les pythagoriciennes.
Rameau (1726)
Jean-Philippe Rameau décrit la façon d'établir ce tempérament dans le dernier chapitre de son second traité intitulé Nouveau système de musique théorique. Il y a sept quintes diminuées d'un quart de comma syntonique et donc quatre tierces pures.
Deux interprétations distinctes du texte original aboutissent à deux tempéraments.
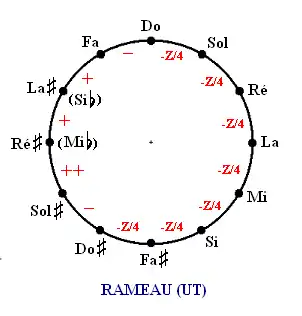
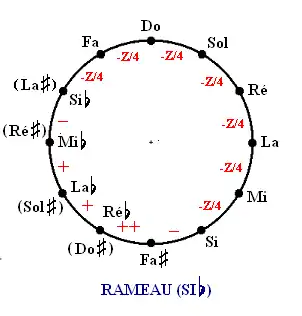
D'autres interprétations tendent vers une compréhension avec une seule option, telle que celle de Benjamin Righetti (article:

Corrette (1753)
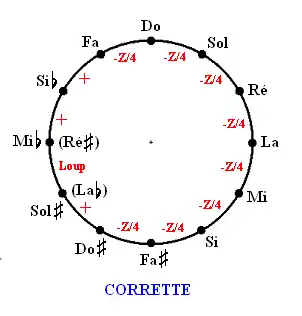
Le tempérament décrit par Michel Corrette est très proche de celui de Chaumont : il possède une quinte réduite en moins ; la conséquence est qu'il y a une quinte forte de plus, le loup devient plus acceptable ce qui permet, à la rigueur, d'utiliser le sol comme la.
On dispose ici de 5 tierces majeures justes : fa-la, do-mi, sol-si, ré-fa et la-do.
Marpourg (1756)
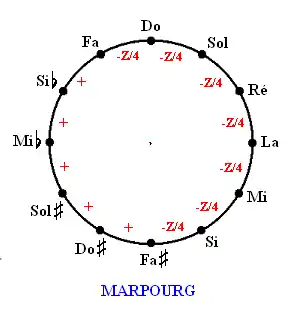
Tempérament à 4 tierces pures. Ce tempérament est considéré à l'époque de Bach par certains auteurs comme la meilleure alternative au tempérament égal. C'est un très bon tempérament, qui à la fois permet la pratique dans toutes les tonalités (mais pas sans colorations « vigoureuses »), et donne de très belles tonalités centrales (doM, solM, réM, voire faM sont les mêmes qu'en mésotonique classique). Il est progressif d'une tonalité à l'autre.
Silbermann
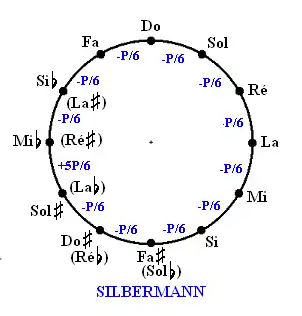
Ce tempérament permet d'avoir huit tierces presque pures (mais trop grandes), les quatre restantes, encore plus grandes, sont proches des tierces pythagoriciennes (-1P/6). Toutes les quintes sont un petit peu courtes, à l'exception de la quinte La♭-Mi♭, trop grande.
Kirnberger
L'intérêt qu'on porte aux tempéraments décrits par Johann Philipp Kirnberger vient de ce que nous sommes, avec lui, dans l'entourage direct de Bach qui, malgré son intérêt pour le « bon tempérament », ne nous a laissé aucun document en clair décrivant sa manière de l'établir. Mais récemment, un musicologue a découvert dans le manuscrit de Le Clavier bien tempéré les indications précises de Bach sur la structure de son tempérament. (article1 et article2, en anglais uniquement)
- Kirnberger I (1760)
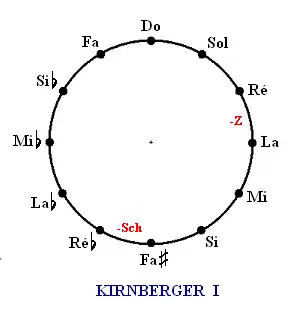
Ce tempérament est extrêmement simple (à expliquer et à réaliser) : en réduisant d'un comma syntonique la quinte ré-la, il assure la pureté de 4 tierces : fa-la, do-mi, sol-si, ré-fa, les autres sont pythagoriciennes, ou pratiquement (le schisma étant placé entre fa et ré).
Dix quintes sont pures — en fait ce tempérament n'est guère différent d'un tempérament pythagoricien avec loup entre ré et la, peut-être plus utile à cet emplacement.
Il ne résout pas très bien la question de la modulation…
Exemple simple de méthode d'accord à l'oreille
- Pour accorder l'instrument : la accordé sur le diapason ; une tierce pure descendante vers fa ; de là, quintes pures montantes vers do, sol, ré - le comma syntonique se trouve placé entre ré et la ; puis quintes pures montées (ou quartes descendues de l'octave supérieure) de la jusque fa et descendantes (ou quartes montées de l'octave inférieure) de fa jusque ré : le schisma se trouve alors placé. Si le diapason est en do, descendre d'une quinte pure vers fa, puis tierce montante pure vers la et on se trouve ramené au problème précédent !
- Kirnberger II - (1771)
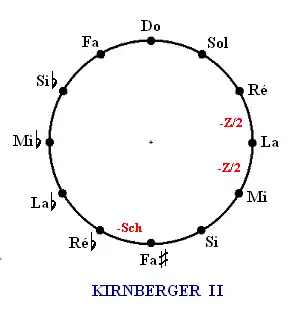
Un peu plus élaboré que le précédent, il répartit le comma syntonique en deux moitiés entre les quintes ré-la et la-mi, le schisma restant placé entre fa et ré. Il est meilleur que le précédent au niveau des modulations, et plus progressif dans l'adoucissement des tierces ; trois d'entre elles sont pures, deux autres sont meilleures que dans la gamme de Pythagore (fa-la et la-do). Il est lui aussi très facile à réaliser à l'oreille (facile avec un diapason au do, un peu plus - guère plus - difficile avec un diapason au la).
- Kirnberger III - (1779)
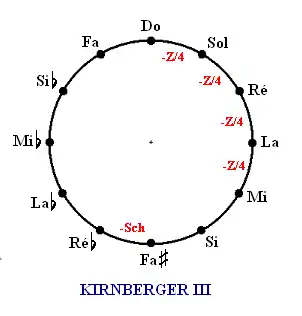
Dans ce tempérament nous avons une seule tierce pure : do-mi. Très simple à réaliser à l'oreille. On partage en quatre le comma syntonique, en tempérant quatre quintes consécutives. On part du la2 situé une octave en dessous du diapason. On baisse le mi au-dessus (mi3) plus faible de 2 battements par seconde. Puis monte le ré3 plus fort de 3 bat./s. On accorde sur ce ré le sol en dessous (sol2) en le montant, la quinte doit battre de 2 bat./s. Sur ce sol on accorde le do3 en le montant de 3 bat./s. On a donc deux quintes faibles et deux quartes fortes. Résultat, la tierce do-mi est pure. Toutes les autres quintes sont accordées pures, c'est-à-dire, do3-fa2, fa2-si♭2, si♭2-mi♭3, mi♭3-la♭2, la♭2-ré♭3; on repart du mi3 et on accorde pures mi3-si2 et si2-fa#2. Le schisma est situé entre les extrémités du cycle : fa#2-réb3 qui bat très légèrement. Ce tempérament est très bon pour les tons en bémols un peu plus tendu pour les dièses[6]. Faire un tempérament par la ou les tierces pures ne donne pas forcément un bon résultat, l'oreille humaine ayant une tolérance de l'intervalle pur. Cette tierce pure doit être le résultat de quatre quintes équilibrées (qui peuvent être une alternance de quinte et quarte à condition de faire les quintes plus étroites que pures et les quartes plus grandes que pures).
Kellner
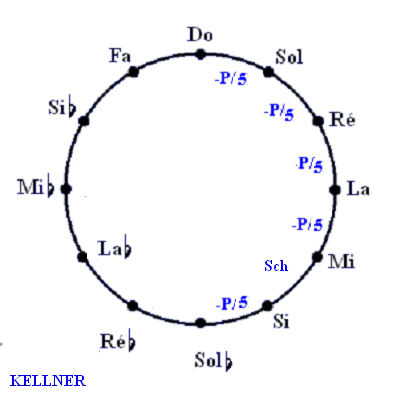
- Le comma pythagoricien est réparti par cinquièmes sur 5 quintes (qui deviennent ainsi un peu courtes) : Do-Sol, Sol-Ré, Ré-La, La-Mi et Si-Sol.
- Ainsi la tierce Do-Mi est assez proche de la pureté, les autres s'en éloignent progressivement et ce tempérament, par le choix de la quinte tempérée Si-Sol favorise les tonalités en bémol.
Il est en fait très proche de Werckmeister III.
Vallotti
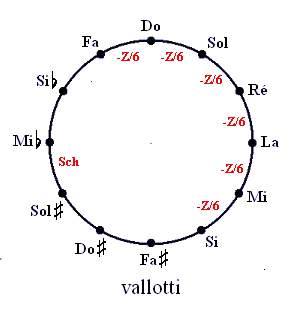 Le tempérament de Vallotti est cité par Tartini en 1754. Il diminue les quintes les plus usuelles (fa-do, do-sol, sol-ré, ré-la, la-mi, mi-si) de 1/6 de comma syntonique chacune – les 6 autres sont inchangées.
Le tempérament de Vallotti est cité par Tartini en 1754. Il diminue les quintes les plus usuelles (fa-do, do-sol, sol-ré, ré-la, la-mi, mi-si) de 1/6 de comma syntonique chacune – les 6 autres sont inchangées.
Les trois tierces fa-la, do-mi et sol-si sont les meilleures, elles différent d’une tierce pure de 1/3 de comma. La qualité des autres tierces diminue progressivement en s’éloignant de celles-ci.
Il subsiste trois tierces (quasiment) pythagoriciennes.
L’ordre pratiqué pour accorder selon ce tempérament place le schisma résiduel entre si et fa.
Ce tempérament, connu également dans une variante (par transposition d'une quinte dans le sens des aiguilles d'une montre de sa structure) appelée « Tartini-Vallotti » est le tempérament le plus utilisé à l'heure actuelle pour la musique baroque, non seulement à cause de son assez grande facilité d'exécution, mais aussi à cause de son caractère peu marqué qui ne choque aucune oreille, étant très intermédiaire entre le tempérament égal et les tempéraments à tierces majeures pures.
- Pour un accord rapide de cette variante, opérer comme suit ; le résultat est un accord en Do, pour La3= 415Hz.
- Prendre un diapason à 440 Hz et accorder le Si. Accorder ensuite en montant, à la quinte pure, le Fa et le Do.
- Puis accorder en descendant du Si, successivement quatre quintes pures. La dernière note accordée est Sol. Nous avons ainsi accordé les six quintes pures du tempérament de Vallotti-Tartini. Bien se familiariser avec les tierces issues de ce début d'accord (La♭-Do, Sol-Si) qui sonnent "tendues" car leur rapport est de 81/64, typique d'une justesse pythagoricienne.::
- Le tempérament proprement dit commence à partir du Sol qu'il vaut mieux appeler désormais Fa. L'accord se continue en descendant de quinte en quinte: Si, Mi, La etc jusqu'au Sol. Pour chaque quinte, après l'avoir accordée pure, la réduire un peu, obtenir un battement lent. Dans cette formule rapide on ne chronomètre pas les battements, on se base sur la qualité de la tierce de la dernière note accordée (par ex: Si-Mi déjà accordé), qui sonnent plus "doux" c'est-à-dire plus proche de la tierce pure (80/64) que les tierces citées au début. Vérifier la quinte Sol-"Do déjà accordé".
- On obtient ainsi un tempérament polyvalent dont le ton le plus juste eu égard aux tierces est Ré Majeur. Les tons voisins sont excellents. Mais le Sol (en fait La issu de quintes pythagoriciennes) est un peu bas, ce qui altère la cadence en La.
Young
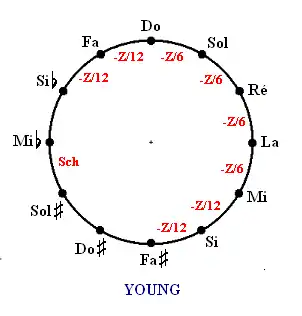
Le tempérament de Young favorise la tierce majeure do-mi, avec 4 quintes réduites d’un 1/6 de comma syntonique. Les 4 quintes plus distantes (si-fa et fa-do ainsi que mi-si et si- fa) ne sont réduites que d’un 1/12 de comma.
La tierce fa-si est la plus mauvaise (quasiment pythagoricienne)
En comparaison du tempérament de Vallotti, la dégradation de la qualité des tierces avec leur éloignement est donc plus progressive. Il reste le schisma entre sol et mi.
Johann Sebastian Bach
La musique de Bach a longtemps fait l’objet d'une controverse autour du type de tempérament que ce dernier utilisait. En effet, celui-ci n’avait laissé aucune indication écrite quant à la façon dont il accordait ses instruments et aucun tempérament connu ne permettait de jouer de façon satisfaisante toute la musique de Bach, de sorte que les avis se partageaient sur le fait qu'il aurait utilisé des tempéraments différents selon ses compositions, ou qu'au contraire, il aurait utilisé un tempérament égal.

En , cependant, un informaticien américain, claveciniste et musicologue : Bradley Lehmann a proposé que le frontispice en haut de la page de garde du Clavier bien tempéré fût justement la description par Bach de son mythique tempérament et y a proposé une « clef » de déchiffrement . Voir le document :
Cette clef résiderait dans la série de volutes irrégulières tracées de la main même du compositeur sur la page de titre d'une partition autographe (ci-contre). Considérées de la droite vers la gauche :
- cinq bouclettes multiplement spiralées correspondraient à cinq quintes réduites d'une portion appréciable de comma,
- les trois suivantes, simples, correspondraient à des quintes pures,
- les trois dernières, doubles, correspondraient à des quintes très légèrement corrigées.
La place du do (noté C en allemand) étant indiquée sur la droite du schéma.
La démonstration de Lehmann est très convaincante et aboutit à un principe de correction des quintes très pertinent (la douzième quinte, entre si et fa serait pure.
Cependant les valeurs précises des corrections restent sujettes à interprétation et à conjectures. Il est vraisemblable que ce tempérament soit dérivé d'un tempérament mésotonique fondé sur des fractions de comma syntonique, comme nombre de tempéraments de l'époque.
Si cette supposition est la bonne, deux hypothèses de corrections sont plausibles : celle d'une correction au 1/6 de comma (hypothèse de Bradley Lehmann) et une au 1/4 de comma, celle du 1/5 de comma étant à écarter.
En effet, si 5 quintes étaient corrigées de 1/5 de comma, l'octave résultante ne s'écarterait de la pureté que d'un schisma au maximum, intervalle suffisamment faible pour ne pas devoir être réparti sur trois autres quintes.
Voici une représentation possible dans l'hypothèse de Lehmann :
Une autre interprétation du frontispice a été proposée par le facteur de clavecin Émile Jobin, qui défend un tempérament au 1/4 de comma. Elle relève d'une longue réflexion qui s'appuie à la fois sur une pratique empirique de l'accord des clavecins et des clavicordes, et sur les observations éclairées du facteur d'orgues Quentin Blumenroeder (notamment de ses relevés de tempéraments sur les orgues historiques). Même s'il fait débat, ce tempérament permet bel et bien de jouer le Clavier bien Tempéré.
L'explication en détail : https://www.clavecin-en-france.org/spip.php?article52
Voir aussi les arguments sur la page http://www.allain-dupre.fr/TEMPERAMENT-Bach-Lehman-Jobin.htm
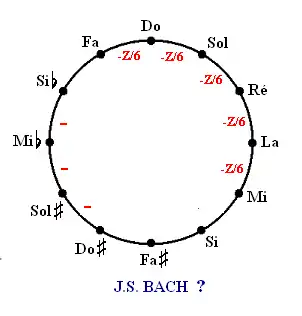
Encore une autre interprétation du frontispice, inspirée par l’hypothèse Jobin, propose le Mésotonique Bien Tempéré, tenant cinq quintes diminuées (sur Do3, Sol2, Ré3, La2, Mi3), ainsi que trois tierces majeures augmentées (Fa2, Do3, Sol2), toutes tenant un même taux de battement d’harmoniques, ayant une valeur absolue strictement égale du point de vue mathématique ; ce taux vaut 1,95 battements par seconde. En plus trois quintes parfaites (Si, Fa#, Do#) et trois quintes très légèrement augmentées (La2b, Mi3b, Si2b), tenant un taux de battements de 0,39 battements par seconde. Le tout est représenté sur le cycle de quintes ci dessous, et expliqué dans le magazine Pianistik No. 111 de décembre 2020, ou dans le texte Proposition d'un algorithme d’évaluation global, des "bons tempéraments", et ceux "de Bach" au site academia.edu, https://expernova.academia.edu/JohanBroekaert.
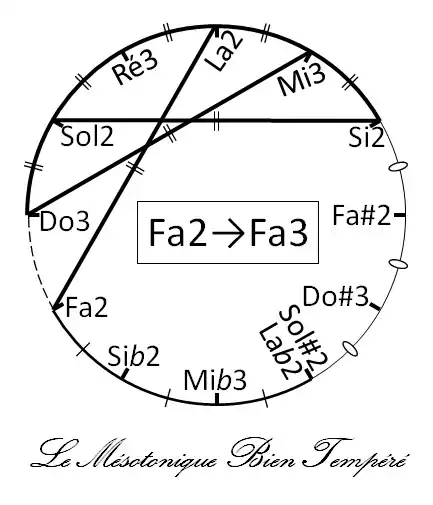
Ce tempérament est facile à accorder auditivement, tel que démontré par la vidéo sur le site https://www.youtube.com/watch?v=lwfESoMxd8Y. La distribution des taux de battements marie parfaitement la distribution des boucles du frontispice Bach, comme on peut voir sur l’image ci-dessous.

Notes et références
- Essai sur la vraie manière de jouer des instruments à clavier, éditions Jean-Claude Lattès en français, 1979, p. 36.)
- Marie Demeilliez, « Tempéraments inégaux et caractères des modes : l’énergique variété des tonalités », Watteau au confluent des arts, éd. C. Barbafieri et C. Rauseo, Valenciennes, 2009, p. 535-551
- (en) http://www-personal.umich.edu/~bpl/larips/informal.html
- Olivier Alain, op. cit page 44
- « Les Tempéraments dans la musique », sur pagesperso-orange.fr (consulté le ).
- Musique et Tempérament Pierre-Yves ASSELIN
Voir aussi
Articles connexes
Liens externes
Bibliographie
Pierre-Yves Asselin, "Musique et tempérament", éditions Costallat 1985, (ISBN 2-905335-009).
Dominique Devie, Le tempérament musical, philosophie, histoire, théorie et pratique, Librairie Musicale Internationale, Marseille (seconde édition 2004).
Jean Lattard, Intervalles, échelles, tempéraments et accordage musicaux, éditions l'Harmattan, , pp. 210-215. (ISBN 2747547477) (le lien suivant permet de consulter librement l'ouvrage : Intervalles, échelles, tempéraments et accordage musicaux).
Herbert Kelletat (Prof.): Zur musikalischen Temperatur (Édition Merseburger). Volume I. Johann Sebastian Bach und seine Zeit (ISBN 3-87537-156-9); Volume II. Wiener Klassik (ISBN 3-87537-187-9); Volume III. Franz Schubert (ISBN 3-87537-239-5).
Heiner Ruland, "Évolution de la musique et de la conscience - Approche pratique des systèmes musicaux", ÉAR, Genève 2005, (ISBN 2-88189-173-X)
Olivier Alain, "L'Harmonie", PUF collection "Que sais-je ?"