Spirale d'Ekman

Lors de l’expédition Fram (1893-1896), pour tenter de rejoindre le Pôle Nord, le norvégien Fridtjof Nansen observa que son navire pris dans le pack arctique dérivait systématiquement à droite de la direction du vent.

L’analyse des observations, faite après l’expédition, montrait que la vitesse de dérive du navire et des glaces de mer de la banquise (il n’y a pas d’icebergs dans cette partie de l’Arctique) était de l’ordre de 2 % de celle du vent, mais dans une direction variant de 20° à 40° à droite de ce dernier. Nansen fit part de ces résultats au Suédois Vilhelm Bjerknes, alors professeur de mécanique des fluides à l’Université d’Oslo et pionnier de la météorologie moderne, qui invita un de ses étudiants, le suédois Vagn Walfrid Ekman, à se pencher sur cette question pour expliquer cet écart de direction.

Ekman soutint ainsi sa thèse en 1902 en examinant l’effet de la friction du vent à la surface supposée plane d’un océan homogène à viscosité constante. Il démontra que cette dérive, vers la droite de la direction du vent, était liée à l’équilibre entre la tension du vent en surface (force de frottement) et la force de Coriolis agissant sur le transport de toute la masse d’eau mise en mouvement, appelé aussi transport d’Ekman. Ekman définit ainsi la spirale qui porte son nom ; celle-ci donne en surface un courant de dérive dévié de 45° à droite de la direction du vent dans l’hémisphère nord (à gauche dans l’hémisphère sud).

Effet de la spirale d'Ekman : vent en bleu, déplacement de l'eau par friction en rouge, déplacement réel en rose (Transport d'Ekman) et force de Coriolis en jaune foncé.

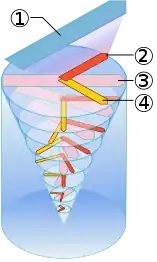
La spirale est une conséquence de la force de Coriolis, de la viscosité du fluide et de la friction de la surface frontière. La figure de droite montre la structure en hélice spiralée du courant de dérive selon l'immersion, dont la projection dans le plan horizontal donne la spirale d'Ekman. On a un vent (bleu) qui met en mouvement la surface de l'eau par friction (rouge). La force de Coriolis (jaune) fait dévier vers la droite (hémisphère nord) le courant ainsi induit et donne un transport de l'eau selon la flèche rose. Cette couche de surface fait bouger la couche sous-jacente mais à une vitesse inférieure à cause de la dissipation par viscosité. Ce nouveau déplacement est lui aussi dévié vers la droite par la force de Coriolis. L'épaisseur de la couche affectée par la spirale dépend de la viscosité de la mer et s'appelle la couche d'Ekman[1].

Les équations qui relient ces forces sont[1] :

${\displaystyle {\begin{aligned}-fv&=-{\frac {1}{\rho _{o}}}{\frac {\partial p}{\partial x}}+K_{m}{\frac {\partial ^{2}u}{\partial z^{2}}},\\fu&=-{\frac {1}{\rho _{o}}}{\frac {\partial p}{\partial y}}+K_{m}{\frac {\partial ^{2}v}{\partial z^{2}}},\\0&=-{\frac {1}{\rho _{o}}}{\frac {\partial p}{\partial z}},\end{aligned}}}$

Où

• p est la pression
• u et v sont les vitesses dans les directions x et y ;
• f est le paramètre local de la force de Coriolis ;
• ${\displaystyle \ K_{m}}$ est le coefficient de diffusion de viscosité.

Cette spirale théorique n'est jamais observée dans la nature. Cependant en mer, une structure spiralée du courant de dérive ou courant d'Ekman a été observée par plusieurs auteurs surtout dans les eaux stratifiées en densité où la thermocline joue un rôle d'écran au transfert de la quantité de mouvement. En d'autres termes, la viscosité est réduite par ce fort gradient vertical de température. Dans ces conditions de stratification, il a été mis en évidence une cohérence très significative, notamment en régime transitoire (coup de vent), entre le vent et le courant dans la couche de mélange avec génération simultanée d'une oscillation d'inertie.

Par contre, dans les zones peu stratifiées, notamment en hiver au moment de la formation en surface des eaux de fond par refroidissement, la turbulence engendrée ne permet pas de constater de relation nette entre vent et courant.

Circulation atmosphérique avec et sans la friction: résultat la spirale d'Ekman

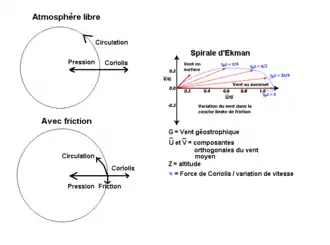
Un fluide comme l'air qui se trouve dans un référentiel en rotation subit deux forces: la différence de pression qui le force à se déplacer vers les pressions les plus basses et la force de Coriolis. Le mouvement est imprimé initialement par la force de pression, la masse d'air "chutant" dans le puits de dépression. La force de Coriolis, qui n'est pas une force réelle mais le résultat de la rotation de la Terre sur le mouvement d'une particule telle que vue par un observateur au sol, "dévie" substantivement ce mouvement perpendiculairement au déplacement de l'air. C'est ce qu'on voit dans la partie gauche supérieure de la figure ci-contre et c'est approximativement ce qui se passe dans la troposphère au-dessus de la couche où la friction du sol s'exerce (500 m à 3 km d'épaisseur selon le terrain).

Dans l'hémisphère nord, la déviation est vers la droite en regardant vers le centre dépressionnaire. À l'équilibre, le courant circule le long des isobares, sans friction. Ce phénomène est décrit par les équations du vent géostrophique qui révèle en particulier la périodicité de telles structures : une onde de Rossby.

Cependant, dans la couche limite, la friction s'ajoute à la balance des forces (partie en bas gauche du dessin) mais dans la direction opposée au déplacement. Ceci ralentit la masse d'air qui par conséquent tombe dans le puits dépressionnaire (de même qu'un satellite en orbite basse en panne de moteur tomberait sur la surface de la terre par friction avec son atmosphère). La partie droite du dessin nous montre la variation de la vitesse en amplitude et en direction en fonction de l'altitude. La friction est maximale au sol et son effet, propagé par la viscosité du fluide, diminue à zéro graduellement en s'élevant. Donc la direction des vents tourne vers la gauche, en faisant face au centre dépressionnaire dans l'hémisphère nord, entre le sommet de la couche limite et le sol. La couche dans laquelle se produit la spirale est aussi appelée la couche d'Ekman.