Scale-invariant feature transform
La scale-invariant feature transform (SIFT), que l'on peut traduire par « transformation de caractéristiques visuelles invariante à l'échelle », est un algorithme utilisé dans le domaine de la vision par ordinateur pour détecter et identifier les éléments similaires entre différentes images numériques (éléments de paysages, objets, personnes, etc.). Il a été développé en 1999 par le chercheur David Lowe.
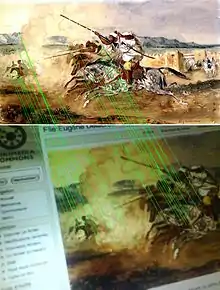
L'étape fondamentale de la méthode proposée par Lowe consiste à calculer ce que l'on appelle les « descripteurs SIFT » des images à étudier. Il s'agit d'informations numériques dérivées de l'analyse locale d'une image et qui caractérisent le contenu visuel de cette image de la façon la plus indépendante possible de l'échelle (« zoom » et résolution du capteur), du cadrage, de l'angle d'observation et de l'exposition (luminosité). Ainsi, deux photographies d'un même objet auront toutes les chances d'avoir des descripteurs SIFT similaires, et ceci d'autant plus si les instants de prise de vue et les angles de vue sont proches. D'un autre côté, deux photographies de sujets très différents produiront selon toute vraisemblance des descripteurs SIFT très différents eux aussi (pouvoir discriminant). Cette robustesse, vérifiée dans la pratique, est une exigence fondamentale de la plupart des applications et explique en grande partie la popularité de la méthode SIFT.
Les applications de la méthode sont nombreuses et ne cessent de s'étendre ; elles couvrent au début du XXIe siècle des domaines tels que la détection d'objet, la cartographie et la navigation, l'assemblage de photos, la modélisation 3D, la recherche d'image par le contenu, le tracking video ou le match moving.
Cet algorithme est protégé aux États-Unis par un brevet détenu par l’université de la Colombie-Britannique.
Origines de la méthode

C'est en 1999 que le chercheur canadien David G. Lowe, professeur à l’université de la Colombie-Britannique, présente lors de la conférence ICCV[1] une nouvelle méthode d'extraction de caractéristiques et de détection d'objets dans des images en niveaux de gris. Le nom de Scale-invariant feature transform (SIFT) a été choisi car la méthode transforme les données d'une image en coordonnées invariantes à l'échelle et rapportées à des caractéristiques locales. Des améliorations et une description précise de la méthode sont proposées par Lowe en 2004 dans la revue International Journal of Computer Vision[2]. L’université de la Colombie-Britannique a demandé et obtenu la protection par brevet de cet algorithme aux États-Unis[3] - [4].
L'idée d'utiliser des points d'intérêt locaux remonte aux travaux de Hans Moravec en 1981 sur la recherche de correspondance entre images stéréoscopiques[5] - [6] et aux améliorations apportées en 1988 par Harris et Stephens[5] - [7]. À la suite de quoi, différents types de caractéristiques sont proposés[1], tels que des segments de lignes[8], des groupements d'arêtes[9] - [10] ou de zones[11]. En 1992, l'intérêt de ce type de détecteur est confirmé par les travaux de Harris[12] et le descripteur de coins qu'il propose, améliorant la plupart des défauts du détecteur de Moravec, va connaître un important succès. Il faut cependant attendre 1997 et le travail précurseur de Cordelia Schmid et Roger Mohr pour établir l'importance, dans le domaine de la vision, des caractéristiques locales invariantes appliquées au problème général de détection et de recherche de correspondance[5] - [13]. Si le descripteur qu'ils développent (et qui s'appuie sur le détecteur de coins de Harris) apporte l'invariance à la rotation, il reste cependant sensible aux changements d'échelle, d'angle d'observation et d'exposition[14]. Lowe comblera grandement ces défauts avec son descripteur SIFT[15].
Généralités
La méthode proposée par Lowe comprend deux parties[15] (chacune ayant fait l'objet de recherches plus ou moins indépendantes par la suite) :
- un algorithme de détection de caractéristiques et de calcul de descripteurs ;
- un algorithme de mise en correspondance proprement dit.
De ces deux aspects, le premier est sans doute celui qui a le plus assuré la popularité de la méthode[16], à tel point que le sigle SIFT fait plus souvent référence aux « descripteurs SIFT » qu'à la méthodologie globale. Il s'agit tout d'abord de détecter sur l'image des zones circulaires « intéressantes », centrées autour d'un point-clé et de rayon déterminé appelé facteur d'échelle. Celles-ci sont caractérisées par leur unité visuelle et correspondent en général à des éléments distincts sur l'image. Sur chacune d'elles, on détermine une orientation intrinsèque qui sert de base à la construction d'un histogramme des orientations locales des contours, habilement pondéré, seuillé et normalisé pour plus de stabilité. C'est cet histogramme qui sous la forme d'un vecteur à 128 dimensions (ou valeurs) constitue le descripteur SIFT du point-clé, et l'ensemble des descripteurs d'une image établissent ainsi une véritable signature numérique du contenu de celle-ci.
Ces descripteurs présentent l'avantage d'être invariants à l'orientation et à la résolution de l'image, et peu sensibles à son exposition, à sa netteté ainsi qu'au point de vue 3D. Ils possèdent ainsi des propriétés similaires à celles des neurones du cortex visuel primaire qui permettent la détection d'objet en intégrant les composantes de base comme les formes, la couleur ainsi que le mouvement [17]. Par exemple, ils décriront de façon très semblable les détails d'une image originale et ceux d'une image retouchée par l'application d'une rotation, d'un recadrage ou d'un lissage, par une correction de l'exposition, par occultation partielle ou encore par l'insertion dans une image plus grande.
Une fois le calcul des descripteurs effectué, l'algorithme de mise en correspondance recherche les zones de l'image qui contiennent des éléments visuellement similaires à ceux d'une bibliothèque d'images de référence, c'est-à-dire des descripteurs numériquement proches. Ceci ne peut fonctionner que parce que les descripteurs SIFT sont à la fois robustes (aux principales transformations affines et aux changements d'exposition ou de perspective) et discriminants (deux objets différents ont une grande probabilité d'avoir des descripteurs différents).
Détection des points-clés et calcul du descripteur SIFT
La première étape de l'algorithme est la détection des points d'intérêt, dits points-clés. Un point-clé est défini d'une part par ses coordonnées sur l'image ( et ) et d'autre part par son facteur d'échelle caractéristique (). En toute rigueur, il s'agit d'une zone d'intérêt circulaire, le rayon de la zone étant proportionnel au facteur d'échelle. Il s'ensuit une étape de reconvergence et de filtrage qui permet d'améliorer la précision sur la localisation des points-clés et d'en éliminer un certain nombre jugés non pertinents. Chaque point-clé restant est ensuite associé à une orientation intrinsèque, c'est-à-dire ne dépendant que du contenu local de l'image autour du point clé, au facteur d'échelle considéré. Elle permet d'assurer l'invariance de la méthode à la rotation et est utilisée comme référence dans le calcul du descripteur, qui constitue la dernière étape de ce processus[18].
Détection d’extrema dans l’espace des échelles
La détection s'effectue dans un espace discret que l'on appelle espace des échelles (scale space) qui comporte trois dimensions : les coordonnées cartésiennes et et le facteur d'échelle . On appelle gradient de facteur d'échelle (noté ) le résultat de la convolution d'une image par un filtre gaussien de paramètre , soit[19] :

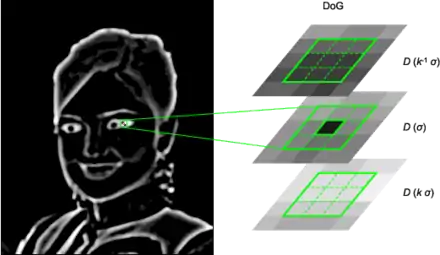
Cette convolution a pour effet de lisser l'image originale de telle sorte que les détails trop petits, c'est-à-dire de rayon inférieur à [note 1], sont estompés. Par conséquent, la détection des objets de dimension approximativement égale à se fait en étudiant l'image appelée différences de gaussiennes (en anglais difference of gaussians, DoG) définie comme suit :
- ,
où est un paramètre fixe de l'algorithme qui dépend de la finesse de la discrétisation de l'espace des échelles voulue[19].
Dans cette image ne persistent plus que les objets observables dans des facteurs d'échelle qui varient entre et . De ce fait, un point-clé candidat est défini comme un point où un extremum du DoG est atteint par rapport à ses voisins immédiats, c'est-à-dire sur l'ensemble contenant 26 autres points défini par :
L'utilisation d'une pyramide est préconisée pour optimiser le temps de calcul des images floutées à un grand nombre d'échelles différentes. La base de la pyramide est en général l'image originale et un niveau donné – on parle d'octave par analogie avec la musique – est obtenu à partir du précédent en divisant la résolution de l'image par 2, ce qui revient à doubler le facteur d'échelle. Au sein d'une même octave, le nombre de convoluées à calculer est constant. Le facteur fixe dans les formules ci-dessus est calculé pour qu'au final, l'espace discrétisé des facteurs d'échelles considérés corresponde à une progression géométrique , avec à chaque changement d'octave une valeur qui devient égale à une quantité de la forme . Ce détail – la progression géométrique des facteurs d'échelle – est important pour que les valeurs des DoG à différentes échelles soient comparables entre elles et il évite, observe Lowe, d'avoir à utiliser un facteur de normalisation dans leur calcul[20].

L'étape de détection des points-clés candidats décrite ci-dessus est une variante de l'une des méthodes de blob detection (détection de zones) développée par Lindeberg, qui utilise le laplacien normalisé par le facteur d'échelle[21] au lieu des DoG. Ces derniers peuvent être considérés comme une approximation des laplaciens et présentent l'avantage d'autoriser l'utilisation d'une technique pyramidale[22].
Localisation précise de points clés

L'étape de détection d’extremums[20] produit en général un grand nombre de points-clés candidats, dont certains sont instables ; de plus, leur localisation, en particulier aux échelles les plus grandes (autrement dit dans les octaves supérieures de la pyramide où la résolution est plus faible) reste approximative. De ce fait, des traitements supplémentaires sont appliqués, pour un objectif double : d'une part, reconverger la position des points pour améliorer la précision sur , et ; d'autre part, éliminer les points de faible contraste ou situés sur des arêtes de contour à faible courbure et donc susceptibles de « glisser » facilement.
Amélioration de la précision par interpolation des coordonnées
Visant à augmenter de façon significative la stabilité et la qualité de la mise en correspondance ultérieure[23], cette étape, qui est une amélioration de l'algorithme original, s'effectue dans l'espace des échelles à trois dimensions, où , qui n'est connu que pour des valeurs discrètes de , et , doit être interpolé.
Cette interpolation s'obtient par un développement de Taylor à l'ordre 2 de la fonction différence de gaussiennes , en prenant comme origine les coordonnées du point-clé candidat[23]. Ce développement s'écrit comme suit :
où et ses dérivées sont évaluées au point-clé candidat et où est un delta par rapport à ce point. Les dérivées sont estimées par différences finies à partir des points voisins connus de façon exacte. La position précise de l'extremum est déterminée en résolvant l'équation annulant la dérivée de cette fonction par rapport à ; on trouve ainsi[23] :
Un delta supérieur à dans l'une des trois dimensions signifie que le point considéré est plus proche d'un des voisins dans l'espace des échelles discret. Dans ce cas, le point-clé candidat est mis à jour et l'interpolation est réalisée à partir des nouvelles coordonnées. Sinon, le delta est ajouté au point candidat initial qui gagne ainsi en précision[24].
Un algorithme de reconvergence similaire a été proposé dans l'implémentation temps-réel basée sur les pyramides hybrides de Lindeberg et Bretzner[25].
Élimination des points-clés de faible contraste
La valeur de aux coordonnées précises du point-clé peut être calculée à partir du développement de Taylor de cette fonction, et constitue donc un extremum local. Un seuillage absolu sur cette valeur permet d'éliminer les points instables, à faible contraste[23] - [note 2].
Élimination des points situés sur les arêtes
Les points situés sur les arêtes (ou contours) doivent être éliminés car la fonction DoG y prend des valeurs élevées, ce qui peut donner naissance à des extremums locaux instables, très sensibles au bruit : si l'image devait subir un changement numérique même imperceptible, de tels points-clés peuvent se retrouver déplacés ailleurs sur la même arête, ou même simplement disparaître[26].
Un point candidat à éliminer, si l'on considère les deux directions principales à sa position, est caractérisé par le fait que sa courbure principale le long du contour sur lequel il est positionné est très élevée par rapport à sa courbure dans la direction orthogonale[26]. La courbure principale est représentée par les valeurs propres de la matrice hessienne :
Les dérivées doivent être évaluées aux coordonnées du point d'intérêt dans l'espace des échelles. Les valeurs propres de sont proportionnelles aux courbures principales de , dont seul le rapport est intéressant. La trace de représente la somme de ces valeurs, le déterminant son produit. Par conséquent, en adoptant un seuil sur le ratio des courbures ( dans la méthode originale de Lowe[2]), un point-clé candidat va être retenu, selon le critère adopté par Lowe, si[26] :
La vérification de ce critère est rapide, ne nécessitant qu'une dizaine d'opérations flottantes seulement. Lorsque ce critère n'est pas vérifié, le point est considéré comme localisé le long d'une arête et il est par conséquent rejeté.
Cette étape est inspirée de la technique de détection de points d'intérêt par l'opérateur de Harris ; pour le seuillage, une matrice hessienne est utilisée au lieu de la matrice des moments d'ordre 2 (tenseur)[26].
Assignation d’orientation
L'étape d'assignation d’orientation consiste à attribuer à chaque point-clé une ou plusieurs orientations déterminées localement sur l'image à partir de la direction des gradients dans un voisinage autour du point. Dans la mesure où les descripteurs sont calculés relativement à ces orientations, cette étape est essentielle pour garantir l'invariance de ceux-ci à la rotation : les mêmes descripteurs doivent pouvoir être obtenus à partir d'une même image, quelle qu'en soit l'orientation[14].
Pour un point-clé donné , le calcul s'effectue sur , à savoir le gradient de la pyramide dont le paramètre est le plus proche du facteur d'échelle du point. De cette façon, le calcul est également invariant à l'échelle. À chaque position dans un voisinage du point-clé, on estime le gradient par différences finies symétriques, puis son amplitude (c.-à-d. sa norme) , et son orientation [14] :
- .
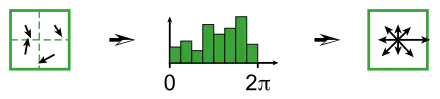
Un histogramme des orientations sur le voisinage est réalisé avec 36 intervalles, couvrant chacun 10 degrés d'angle. Chaque voisin est doublement pondéré dans le calcul de l'histogramme : d'une part, par son amplitude ; d'autre part, par une fenêtre circulaire gaussienne de paramètre égal à 1,5 fois le facteur d'échelle du point-clé. Les pics dans cet histogramme correspondent aux orientations dominantes. Toutes les orientations permettant d'atteindre au moins 80 % de la valeur maximale sont prises en considération, ce qui provoque si nécessaire la création de points-clés supplémentaires ne différant que par leur orientation principale[14].
À l'issue de cette étape, un point-clé est donc défini par quatre paramètres . Il est à noter qu'il est parfaitement possible qu'il y ait sur une même image plusieurs points-clés qui ne différent que par un seul de ces quatre paramètres (le facteur d'échelle ou l'orientation, par exemple).
Descripteur de point-clé
Une fois les points-clés, associés à des facteurs d'échelles et à des orientations, détectés et leur invariance aux changements d'échelles et aux rotations assurée, arrive l'étape de calcul des vecteurs descripteurs, traduisant numériquement chacun de ces points-clés. À cette occasion, des traitements supplémentaires vont permettre d'assurer un surcroît de pouvoir discriminant en rendant les descripteurs invariants à d'autres transformations telles que la luminosité, le changement de point de vue 3D, etc. Cette étape est réalisée sur l'image lissée avec le paramètre de facteur d'échelle le plus proche de celui du point-clé considéré[27].
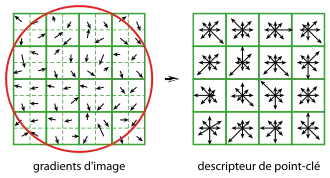
Autour de ce point, on commence par modifier le système de coordonnées local pour garantir l'invariance à la rotation, en utilisant une rotation d'angle égale à l'orientation du point-clé, mais de sens opposé. On considère ensuite, toujours autour du point-clé, une région de 16 × 16 pixels, subdivisée en 4 × 4 zones de 4 × 4 pixels chacune. Sur chaque zone est calculé un histogramme des orientations comportant 8 intervalles. En chaque point de la zone, l'orientation et l'amplitude du gradient sont calculés comme précédemment. L'orientation détermine l'intervalle à incrémenter dans l'histogramme, ce qui se fait avec une double pondération – par l'amplitude et par une fenêtre gaussienne centrée sur le point clé, de paramètre égal à 1,5 fois le facteur d'échelle du point-clé[28].
Ensuite, les 16 histogrammes à 8 intervalles chacun sont concaténés et normalisés. Dans le but de diminuer la sensibilité du descripteur aux changements de luminosité, les valeurs sont plafonnées à 0,2 et l'histogramme est de nouveau normalisé, pour finalement fournir le descripteur SIFT du point-clé, de dimension 128[29].
Cette dimension peut paraître bien élevée, mais la plupart des descripteurs de dimension inférieure proposés dans la littérature présentent de moins bonnes performances dans les tâches de mise en correspondance[29] pour un gain en coût de calculs bien modéré, en particulier quand la technique Best-Bin-First (BBF) est utilisée pour trouver le plus proche voisin. Par ailleurs, des descripteurs de plus grande dimension permettraient probablement d'améliorer les résultats, mais les gains escomptés seraient dans les faits assez limités, alors qu'à l'inverse augmenterait sensiblement le risque de sensibilité à la distorsion ou à l'occultation. Il a également été démontré que la précision de recherche de correspondance de points dépasse 50 % dans les cas de changement de point de vue supérieur à 50 degrés, ce qui permet d'affirmer que les descripteurs SIFT sont invariants aux transformations affines modérées. Le pouvoir discriminant des descripteurs SIFT a pour sa part été évalué sur différentes tailles de bases de données de points-clés ; il en ressort que la précision de mise en correspondance est très marginalement affectée par l'augmentation de la taille de la base de données, ce qui constitue une bonne confirmation du pouvoir discriminant des descripteurs SIFT[30].
Utilisation pour la recherche d'objets dans des images
La problématique de base pour laquelle la méthode SIFT a été conçue est la suivante : peut-on trouver dans une image donnée (dite image question ou image suspecte), des objets déjà présents dans une collection d'images de référence préétablie ?
Dans la méthode originale de David Lowe[1] - [2], les points-clés et les descripteurs SIFT sont tout d'abord extraits des images de référence et stockés dans une sorte de base de données. Un objet est identifié dans l'image question en effectuant une comparaison de ses descripteurs à ceux des images de référence disponibles en base de données, fondée simplement sur la distance euclidienne. Parmi toutes les correspondances ainsi établies, des sous-ensembles (clusters) sont identifiés, au sein desquels la mise en correspondance est cohérente du point de vue des positions des points, des facteurs d'échelle et des orientations. Les clusters contenant au moins trois correspondances ponctuelles sont conservés. Dans chacun d'eux, on modélise la transformation permettant de passer de l'image question à l'image de référence, et on élimine les correspondances aberrantes par simple vérification de ce modèle. Enfin, Lowe applique un modèle probabiliste pour confirmer que la détection d'une correspondance d'objets entre l'image question et l'une des images de référence n'est pas due au hasard, basé sur l'idée que si de nombreux points n'ont pas pu être mis en correspondance c'est que l'on a peut-être affaire à un faux positif[31].
À chacune de ces étapes, Lowe[2] propose une approche efficace présentée succinctement dans le tableau ci-dessous et dont les principes sont détaillés dans les paragraphes suivants.
| Étape | Techniques utilisées | Avantages |
|---|---|---|
| Extraction des points-clés (des images de référence et de l'image question) | Pyramide de gradients, différence de gaussiens, assignation d’orientation | Précision, stabilité, invariance aux modifications d’échelle et à la rotation |
| Calcul des descripteurs (des images de référence et de l'image question) | Échantillonnage et lissage des plans locaux d’orientation de l’image | Stabilité relative aux transformations affines et à la luminosité |
| Indexation des descripteurs des images de référence | Arbre kd | Efficacité |
| Recherche des correspondances avec les descripteurs de l'image question | Plus proche voisin approximatif (Best Bin First) | Rapidité |
| Identification de clusters | Transformée de Hough et table de hachage | Modèle de transformation fiable |
| Vérification du modèle | Moindres carrés linéaires | Élimination des fausses correspondances |
| Validation de l'hypothèse | Inférence bayésienne | Fiabilité |
Indexation des descripteurs et recherche de correspondances
L’indexation est l’opération de stockage des descripteurs SIFT des images de référence, d'une manière qui facilite l’identification des descripteurs correspondants de l'image question. Lowe utilise un arbre kd pour indexer les descripteurs puis une méthode de recherche dans cet arbre modifiée par rapport à l'approche classique, appelée Best bin first[32]. Cette dernière est capable de trouver les plus proches voisins d'un descripteur question avec une bonne probabilité de façon très économe en temps de calcul. Cet algorithme se fonde sur deux astuces. Tout d'abord, le nombre de boîtes (feuilles de l'arbre kd) à explorer pour trouver le plus proche voisin d'un descripteur question donné est limité à une valeur maximale fixée, par exemple à 200. Ensuite, les nœuds de l'arbre kd sont explorés dans l'ordre de leur distance au descripteur question, grâce à l'utilisation d'une file de priorité basée sur un tas binaire. Par distance d'un nœud à un descripteur, on entend distance euclidienne de la boîte englobante des feuilles sous-jacentes à ce descripteur. Dans la plupart des cas, ce procédé fournit la meilleure correspondance, et, dans les cas restants, un descripteur très proche de celle-ci[33].
De façon à déconsidérer les descripteurs faiblement discriminants (parce qu'ils sont trop souvent présents dans la base de référence, comme par exemple ceux qui sont extraits de motifs d'arrière-plan souvent répétés dans les images), Lowe recherche à la fois le plus proche voisin et le second plus proche voisin de chaque descripteur question. Lorsque le rapport des distances est supérieur à 0,8, la correspondance est éliminée, car considérée comme ambiguës (« bruit »). Par ce critère, Lowe parvient à éliminer 90 % des fausses correspondances en perdant moins de 5 % de correspondances correctes[34].
Identification de clusters par la transformée de Hough
On appelle pose d'un objet le point de vue sous lequel il est photographié, c'est-à-dire sa position dans l'espace par rapport à un repère absolu. En général, la base des images de référence contient différentes poses d'objets identiques. Chaque correspondance individuelle entre points-clés obtenue à l'étape précédente constitue une hypothèse quant à la pose de l'objet sur l'image question par rapport à l'image de référence concernée. Il s'agit donc maintenant de grouper les hypothèses cohérentes entre elles de façon à mettre en correspondance les objets des images et non plus seulement des points isolés. La transformée de Hough est utilisée pour cela. Elle identifie des groupes de correspondances, que l'on appelle clusters, par un système de vote[34].
Alors qu'un objet rigide possède en général six degrés de liberté dans l'espace (trois rotations, trois translations), une correspondance de points-clés entre deux images ne permet de relier que quatre paramètres (deux paramètres de position, l'angle et l'échelle) et constitue donc une approximation parmi toutes les poses possibles. Le sous-espace des poses ainsi paramétré est segmenté en boîtes de façon assez grossière : Lowe utilise des intervalles de 30 degrés pour l’orientation, un facteur de 2 pour l’échelle et 0,25 fois la dimension maximale de l’image de référence concernée (compte tenu du rapport d'échelles) pour la position[2]. Chaque correspondance vote pour la boîte associée. Les correspondances concernant les facteurs d'échelles les plus élevés, considérées comme plus pertinentes, se voient attribuer un poids double de celles concernant les facteurs les plus bas. En outre, pour éviter les effets de bord lors de l’assignation des boîtes, chaque correspondance vote pour les 2 plus proches intervalles dans chaque dimension, c'est-à-dire qu'elle vote 16 fois[34].
Lors de l'implémentation, Lowe recommande l'utilisation d'une table de hachage pour éviter de représenter toutes les boîtes possibles en mémoire dont seulement un petit nombre risque d'être non vide[34].
Lorsque plusieurs correspondances votent pour une même boîte, c'est-à-dire pour la même pose d’un objet, la probabilité que la correspondance soit correcte est largement supérieure à ce que pourrait donner une correspondance isolée. Ainsi, les boîtes contenant au moins trois entrées sont considérées comme des clusters fiables, et retenus pour la suite de l'analyse[34].
Vérification du modèle par la méthode des moindres carrés
Les clusters obtenus sont soumis à une procédure de vérification par l’application de la méthode des moindres carrés aux paramètres de la transformation affine reliant le modèle (image de référence) à l’image question[35]. La transformation affine d’un point modèle en un point image peut s’écrire ainsi :
- ,
où est la translation du modèle, et où les paramètres , , et modélisent la transformation vectorielle (qui peut être une rotation à l'origine, une similitude, une distorsion, etc.) Pour obtenir les paramètres de la transformation, l’équation ci-dessus est réécrite de manière à regrouper les inconnues dans un vecteur-colonne :
Cette équation représente une seule correspondance. Pour obtenir les autres correspondances, il suffit de rajouter pour chacune d’elles deux lignes à la matrice et deux coefficients au second membre. Trois correspondances au minimum sont requises pour espérer une solution. Le système linéaire complet s’écrit alors :
où est une matrice connue (vérifiant généralement ), un vecteur inconnu de paramètres de dimension et enfin un vecteur connu de mesures de dimension .
Ce système n'a en général pas de solution exacte puisqu'il est sur-dimensionné ; mais ce qui nous intéresse est qu'il est possible d'en trouver une pseudo-solution au sens des moindres carrés, c'est-à-dire un vecteur qui minimise l'erreur , et qui est aussi solution de l’« équation normale » :
La solution du système d’équations linéaires, qui s'exprime grâce à la matrice , dite pseudo-inverse de Moore-Penrose de , est donnée par :
Elle minimise la somme des carrés des distances entre les positions des points-clés calculées à partir de la transformée des positions du modèle, et les positions correspondantes sur l'image cible[35].
Les données aberrantes peuvent ensuite être écartées en vérifiant la concordance de chaque correspondance avec la solution des moindres carrés. Sont éliminées les correspondances qui se situent au-delà de la moitié de l’intervalle d’erreur utilisé pour la discrétisation de l'espace des poses dans la transformée de Hough. Une nouvelle solution par la méthode des moindres carrés est calculée à partir des points restants, et le processus est itéré plusieurs fois. Il est également possible grâce à la transformation estimée par la méthode des moindres carrés de récupérer des correspondances qui avaient été manquées précédemment. À la fin du processus, s’il reste moins de 3 points après suppression des points aberrants, alors la correspondance est dite infructueuse et rejetée[36].
Validation finale par inférence bayésienne
La décision finale d’admission ou de rejet d’une mise en correspondance d'objets (hypothèse) se fait sur la base d’un modèle probabiliste[37]. Cette méthode détermine en premier lieu le nombre attendu de fausses correspondances, connaissant la taille estimée du modèle, le nombre de points-clés dans la région et la précision de la correspondance. Une analyse par inférence bayésienne donne ensuite la probabilité que l’objet trouvé sur l'image de référence soit effectivement présent dans l'image question à partir du nombre de vraies correspondances trouvées. Une hypothèse est acceptée si cette probabilité est supérieure à 0,98. À l'exception d'images présentant de grands écarts de luminosité ou des objets ayant subi des transformations sévères ou non rigides, la détection d’objet au moyen de la méthode SIFT parvient ainsi à d'excellents résultats[36].
Comparaison des descripteurs SIFT aux autres descripteurs locaux
Plusieurs études d’évaluation des performances de différents descripteurs locaux (notamment le descripteur SIFT) ont été menées, dont les principales conclusions sont[38] :
- les caractéristiques SIFT et apparentées (en particulier GLOH) donnent les meilleurs taux de rappel pour des transformations affines de moins de 50 degrés ; au-delà de cette limite, les résultats deviennent incertains ;
- le caractère discriminant des descripteurs est mesuré en sommant leurs valeurs propres, obtenues par analyse en composantes principales appliquée à ces descripteurs normalisés par leur variance ; cela traduit dans les faits la quantité de variance « capturée » par les différents descripteurs et, partant, leur pouvoir discriminant ; les caractéristiques PCA-SIFT, GLOH et SIFT donnent les meilleurs résultats ;
- les descripteurs à base de SIFT dépassent en performance les autres types de descripteurs locaux en présence de scènes texturées ou, dans une moindre mesure, de scènes structurées ;
- les descripteurs à base de SIFT dépassent en performance les autres descripteurs dans le cas d'images texturées ou structurées ayant subi un changement d'échelle d'un ratio compris entre 2 et 2,5 ou une rotation comprise entre 30 et 45 degrés ;
- les performances de tous les descripteurs, et notamment ceux basé sur l'analyse des contours, tel que shape context, se dégradent en présence d'images ayant subi un floutage substantiel (du fait de l'estompage des contours) ; en tout état de cause, les descripteurs GLOH, PCA-SIFT et SIFT sont ceux qui présentent les meilleures performances de tous les descripteurs étudiés. Il en est de même dans les situations de modifications d'illumination.
Il ressort de ces études que les descripteurs à base de SIFT, du fait de leur plus grande robustesse et de leur meilleur pouvoir discriminant, sont particulièrement adaptés à la recherche de correspondances.
Des descripteurs plus récents, tel que SURF, n'ont cependant pas été pris en compte dans ces études, quoiqu'une étude ultérieure ait montré que ce dernier avait des performances similaires à celles de SIFT tout en étant sensiblement plus rapide[39].
Une nouvelle variante du descripteur SIFT, basée sur un histogramme irrégulier, a récemment été proposée[40], apportant une nette amélioration des performances. Au lieu d'utiliser des grilles de boîtes d'histogrammes de 4 × 4, toutes les boîtes sont ramenées au centre de la caractéristique, d'où une amélioration significative de la robustesse aux changements d'échelle.
Enfin, comparée au descripteur SIFT standard, la technique SIFT-Rank s'est révélée avoir de meilleures performances[41]. Un descripteur SIFT-Rank est généré à partir d'un descripteur SIFT standard, en fixant chaque boîte d'histogramme à son rang dans un tableau de boîtes. La distance euclidienne entre les descripteurs SIFT-Rank est invariante aux modifications monotones arbitraires dans les valeurs des boîtes d'histogramme, et elle est liée à la corrélation de Spearman[41].
Applications des descripteurs SIFT
Outre la reconnaissance d'objet, les avantageuses propriétés des descripteurs SIFT (caractère discriminant, invariance à la translation, à la rotation et au changement d'échelle et robustesse aux transformations affines en général (distorsions), aux changements de points de vue 3D ainsi qu'aux changements de luminosité) en font un excellent choix pour d'autres applications dont quelques-unes sont énumérées ici.
Localisation de robot en environnement inconnu
Le but de cette application est de fournir une solution robuste et fiable au problème de localisation de robots en environnement inconnu[42]. Un système de stéréoscopie trinoculaire est utilisé pour estimer les positions 3D des points-clés déterminés. Un point-clé n'est pris en compte que s'il apparaît simultanément sur les trois images du système trinoculaire, et à condition que les disparités entre ces images ne soient pas handicapantes, afin de générer le moins possible de données aberrantes[43]. En mouvement, le robot se localise en comparant les caractéristiques vues avec celles de la carte 3D qu'il a en mémoire ; il enrichit au fur et à mesure cette carte de nouvelles caractéristiques et met à contribution un filtre de Kalman pour mettre à jour leurs positions tridimensionnelles[43].
L’assemblage de panoramas
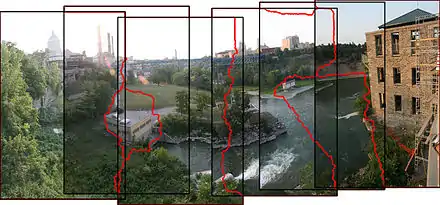
La mise en correspondance de points d'intérêt par la méthode SIFT peut être utilisée comme première étape d'un processus d'assemblage de photos entièrement automatisé. Cette application consiste à construire une image panoramique unique à partir de prises de vues successives d'un même sujet (souvent un paysage) décalées les unes des autres par un déplacement dans l'espace. La technique proposée par Brown et Lowe en 2003[44] a l'avantage de fonctionner sur une collection d'images, sans qu'aucune connaissance a priori ne soit nécessaire sur l'endroit précis de la prise de vue de chacune de ces images, ni même leur ordre ; elle peut aussi exclure de l'assemblage des images qui n'auraient rien à voir avec un panorama donné et même reconstituer en même temps plusieurs panoramas indépendants.
L'idée de l'application est la suivante[44]. Les descripteurs SIFT sont extraits de chacune des images à étudier et mis en correspondance les uns avec les autres (recherche des plus proches voisins comme dans la méthode SIFT générale). On construit ensuite un graphe dont les sommets sont les différentes images et l'on ajoute des arêtes entre les images qui ont le plus de points-clés en correspondance. Cela signifie qu'elles ont potentiellement des éléments du décor en commun. Pour en être sûr, on essaie de déterminer la transformation géométrique permettant de passer de l'une à l'autre, ou homographie, en utilisant un RANSAC entre les points. En cas de succès, la paire d'images est soumise à une vérification supplémentaire basée sur un modèle probabiliste et destinée à s'assurer que les correspondances ne sont pas dues au hasard. Seules sont conservées dans le graphe les arêtes qui passent le test. Les composantes connexes correspondent alors à autant de panoramas indépendants, qui sont assemblés séparément. Pour cela, une technique dite d'« ajustement de faisceaux » (bundle adjustment) est utilisée pour déterminer les paramètres objectifs de la caméra lors de la prise de vue de chaque image, par rapport au panorama global. Une fois que cet ajustement est fait, il est théoriquement possible d'obtenir la valeur de chacun des pixels du panorama global à partir des images de départ. Pour la construction finale, on applique une pondération et un lissage liés à la nécessité d'harmoniser l'exposition des images de départ, de telle sorte que les grandes étendues uniformes (cieux, etc.) ne présentent pas trop de variations dans leur luminosité tout en s'assurant que les détails ne seront pas perdus. Cette technique sophistiquée s'appelle assemblage multi-bande (multi band blending).
La technique a donné naissance au logiciel Autostitch[45].
Modélisation, reconnaissance et suivi d'objets 3D
Cette problématique consiste à déterminer la position exacte d'une caméra à partir des images qu'elle acquiert, simplement en analysant l'orientation et la position d'un objet précis apparaissant dans son champ de vision. Les applications en sont diverses ; la plus populaire étant sans doute la réalité augmentée, qui consiste à intégrer de nouveaux objets au sein d'une scène filmée, par exemple une bouteille sur une table dès que ladite table apparaît dans le champ de la caméra, et cela si possible en temps réel.
Une façon de traiter cette application a été proposée par Gordon et Lowe en 2006[46]. Elle comprend une phase d'apprentissage qui permet d'établir une modélisation 3D de l'objet témoin à partir de l'analyse de différentes prises de vues 2D de celui-ci. Les descripteurs SIFT sont utilisés pour mettre en relation les points-clés entre différentes images et construire un modèle 3D de l'objet (mise en correspondance dite « 2D-to-3D »). Une fois cette phase effectuée, on extrait de chaque image filmée les descripteurs SIFT et on les met en correspondance avec ceux des images de référence, de manière à obtenir les correspondances « 2D-to-3D » de l'image filmée. La position de la caméra est alors déterminée par une technique de RANSAC améliorée (Levenberg-Marquardt) qui minimise l'erreur de projection.
Descripteurs SIFT 3D pour la reconnaissance de mouvements humains
Des extensions au descripteur SIFT aux données spatio-temporelles de dimension 2+1, dans le contexte de reconnaissance de mouvements humains dans des séquences vidéo, ont été proposées dans la littérature scientifique[47] - [48] - [49]. Le calcul d'histogrammes dépendants de positions locales est étendu, dans l'algorithme SIFT, de 2 à 3 dimensions pour adapter les caractéristiques SIFT au domaine spatio-temporel. Pour réaliser une reconnaissance de mouvements humains dans une séquence vidéo, un échantillonnage de vidéos d'apprentissage est effectué soit à des points d'intérêt spatio-temporel, soit à des positions, instants et échelles aléatoirement choisis. Les régions spatio-temporelles autour de ces points d'intérêt sont décrites au moyen du descripteur SIFT 3D. Ces descripteurs sont enfin rangés en clusters formant un modèle de sac de mots spatio-temporel. Les descripteurs SIFT 3D extraits des vidéos de test sont enfin comparés à ces « mots ».
Les auteurs confirment l'obtention de meilleurs résultats grâce à cette approche à base de descripteur 3D que par les autres approches utilisant de simples descripteurs SIFT 2D ou les magnitudes de gradients[50].
Analyse du cerveau humain au moyen d’images RMN 3D
La morphométrie basée sur des descripteurs d'image (FBM, feature based morphometry), est une technique d'analyse et de classification d'images 3D du cerveau humain obtenus par résonance magnétique[51]. Grâce à la technique SIFT, l'image est vue comme un assemblage géométrique de structures indépendantes (zones d'intérêt). En utilisant un modèle probabiliste assez fin et en se basant sur l'observation de différentes classes de sujets dûment étiquetés, par exemple des sujets sains d'un côté et des sujets atteints de la maladie d'Alzheimer de l'autre, la technique FBM parvient à regrouper les structures similaires d'une image à l'autre et à les classifier selon l’étiquetage. Un système ainsi entraîné devient capable d'étiqueter automatiquement une image étrangère : sur un ensemble de test constitué d'environ 200 images IRM du cerveau humain, la détection des cas sains et des cas atteints de la maladie d'Alzheimer est correcte dans 80 % des cas, précisent les auteurs.
Variantes et extensions
- RIFT
- RIFT[52] est une variante de SIFT adaptée aux images texturées sur lesquelles la notion d'orientation principale n'a pas vraiment de sens, tout en étant invariante aux rotations. Le descripteur est construit en utilisant des patches circulaires normalisés divisés en anneaux également circulaires et d’égale largeur ; un histogramme d’orientation de gradient est calculé à partir de chacun de ces anneaux. Pour garantir l’invariance à la rotation, l'orientation est mesurée pour chaque point du centre vers l’extérieur.
- G-RIF
- G-RIF[53] (ou Generalized robust invariant feature) est un descripteur de contexte regroupant les orientations des contours, les densités des contours et les informations de teintes dans une forme unifiée, combinant information perceptive et codage spatial. Une nouvelle méthode de classification est utilisée, basée sur un modèle probabiliste utilisant les votes des descripteurs locaux dans un voisinage.
- SURF
- Présenté comme une solution de hautes performances capable de d’approcher et même de dépasser les schémas précédents du point de vue répétitivité, distinctivité et robustesse, SURF[54] (ou Speeded Up Robust Features) est un détecteur de points d’intérêts invariant aux changements d’échelle et aux rotations. Afin de réduire les temps de traitement, il fait usage d'images intégrales pour le calcul de la convolution, et reprend les points forts des meilleurs détecteurs et descripteurs l’ayant précédé, en utilisant des mesures à base de matrices hessiennes rapides pour le détecteur et un descripteur basé sur les distributions. Il décrit une distribution de réponses d’ondelettes de Haar dans le voisinage du point d’intérêt. Seulement 64 dimensions sont utilisées, ce qui permet de réduire le temps de calcul des caractéristiques et de recherche des correspondances. L’étape d’indexation est basée sur le signe du Laplacien, d’où l'accélération de la recherche de correspondances et l’amélioration de la robustesse du descripteur.
- PCA-SIFT et GLOH
- PCA-SIFT[55] et GLOH[56] sont des variantes de SIFT. Le descripteur PCA-SIFT est un vecteur de gradients d’image dans les directions et calculé à l’intérieur de la région de support. La région du gradient est échantillonnée en 39 × 39 positions, générant un vecteur de dimension 3042. Cette dimension est réduite à 20 par la méthode d’analyse en composantes principales[57]. GLOH (pour Gradient location-orientation histogram) est une extension du descripteur SIFT dont la robustesse et le caractère distinctif ont été améliorés. Comparé à SIFT, le descripteur GLOH est calculé à partir d’une grille de positions log-polaires avec trois boîtes en direction radiale (de rayons 6, 11 et 15) et huit en direction angulaire, soit 17 boîtes de position. La boîte centrale n’est pas divisée dans les directions angulaires. Les orientations des gradients sont quantifiées en 16 boîtes, d’où 272 histogrammes de boîtes. Ici aussi la taille du descripteur est réduite au moyen de l’analyse en composantes principales. La matrice de variance-covariance de l’ACP est estimée sur les patches d’image collectés de différentes images. Les 128 plus importants vecteurs propres sont utilisés pour la description.
- Autres méthodes
- Une équipe formée autour de Wagner a développé deux algorithmes de détection d’objet spécialement pensés pour tenir compte des limitations techniques des photophones[58], mettant en œuvre le détecteur de coins FAST pour la détection de caractéristiques. Les deux algorithmes distinguent deux phases : une phase de préparation hors-ligne, au cours de laquelle les caractéristiques sont calculées pour différents niveaux d’échelles, et une phase de traitement en ligne, au cours de laquelle seules les caractéristiques du niveau d’échelle fixé de la photographie issue du photophone sont calculées. De plus, des caractéristiques sont obtenues à partir d’une imagette d’une taille fixe de 15 × 15 pixels, formant un descripteur SIFT réduit à 36 dimensions[59]. Cette approche a été ensuite améliorée par l’intégration d’un arbre de vocabulaire évolutif dans le pipeline de détection[60]. Il s’ensuit une meilleure reconnaissance des objets sur les photophones. Le principal inconvénient de cette approche est son important besoin de mémoire vive[61].
Notes et références
Notes
- Ici comme dans la littérature scientifique en général, le facteur d'échelle – paramètre du filtre gaussien – est assimilé à une distance en pixels sur l'image, que l'on pourrait appeler rayon associé . En fait, ils sont proportionnels (), avec un facteur qui varie généralement entre 3 et 4 selon les auteurs. Il est tout simplement lié au nombre de coefficients au-delà duquel les valeurs de la gaussienne deviennent négligeables.
- Il est à noter que dans la méthodologie originale de Lowe, le point-clé candidat est éliminé si la valeur de est inférieure à 0,03 (en valeur absolue).
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Scale-invariant feature transform » (voir la liste des auteurs).
- (en) David G. Lowe, « Object recognition from local scale-invariant features », dans Proceedings of the International Conference on Computer Vision, vol. 2, (lire en ligne), p. 1150–1157.
- (en) David G. Lowe, « Distinctive image features from scale-invariant keypoints », International Journal of Computer Vision, vol. 60, no 2, , p. 91–110 (lire en ligne).
- (en) Om K. Gupta et Ray A. Jarvis, « Using a Virtual World to Design a Simulation Platform for Vision and Robotic Systems », dans Proceedings of the 5th International Symposium on Advances in Visual Computing, Springer Verlag, (ISBN 978-3-642-10330-8, lire en ligne), p. 241.
- (en) Brevet U.S. 6,711,293, « Method and apparatus for identifying scale invariant features in an image and use of same for locating an object in an image ».
- Lowe (2004), p. 93.
- (en) Hans P. Moravec, « Rover Visual Obstacle Avoidance », dans Proceedings of the seventh International Joint Conference on Artificial Intelligence, Vancouver, Colombie Britannique, (lire en ligne), p. 785-790.
- (en) Chris Harris et Mike Stephens, « A combined corner and edge detector », dans Proceedings of the fourth Alvey Vision Conference, Manchester, (lire en ligne), p. 147–151.
- (en) W. E. L. Grimson et Thomas Lozano-Pérez, « Localizing overlapping parts by searching the interpretation tree », IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-9, no 4, , p. 469–482.
- (en) David G. Lowe, « Three-dimensional object recognition from single two-dimensional images », Artificial Intelligence, vol. 31, no 3, , p. 355–395 (lire en ligne).
- (en) Randal C. Nelson et Andrea Selinger, « Large-scale tests of a keyed, appearance-based 3-D object recognition system », Vision Research, vol. 38, no 15, , p. 2469–2488 (lire en ligne).
- (en) Ronen Basri et David. W. Jacobs, « Recognition using region correspondences », International Journal of Computer Vision, vol. 25, no 2, , p. 141–162 (lire en ligne).
- C. Harris, « Geometry from visual motion », dans A. Blake and A. Yuille, Active Vision, MIT Press, , p. 263-284.
- (en) C. Schmid et R. Mohr, « Local grayvalue invariants for image retrieval », IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 19, no 5, , p. 530-534 (lire en ligne).
- Lowe (2004), p. 103.
- Lowe (2004), p. 91.
- (en) Marco Treiber, An introduction to object recognition : selected algorithms for a wide variety of application, Springer, , 202 p. (ISBN 978-1-84996-234-6, lire en ligne), p. 147.
- (en) T. Serre, M. Kouh, C. Cadieu, U. Knoblich, G. Kreiman et T. Poggio, « A Theory of Object Recognition: Computations and Circuits in the Feedforward Path of the Ventral Stream in Primate Visual Cortex », Computer Science and Artificial Intelligence Laboratory Technical Report, no MIT-CSAIL-TR-2005-082, (lire en ligne).
- Lowe (2004), p. 92.
- Lowe (2004), p. 95.
- Lowe (2004), p. 97.
- (en) Tony Lindeberg, « Feature detection with automatic scale selection », International Journal of Computer Vision, vol. 30, no 2, , p. 79–116 (lire en ligne).
- Lowe (2004), p. 96.
- Lowe (2004), p. 100.
- Lowe (2004), p. 101.
- (en) Tony Lindeberg et Lars Bretzner, « Real-time scale selection in hybrid multi-scale representations », dans Proceedings of the 4th international conference on Scale space methods in computer vision, vol. 2695, Berlin, Springer-Verlag, (ISBN 3-540-40368-X, lire en ligne), p. 148–163.
- Lowe (2004), p. 102.
- Lowe (2004), p. 104.
- Lowe (2004), p. 105.
- Lowe (2004), p. 106.
- Lowe (2004), p. 107.
- Lowe (2004), p. 109.
- (en) Jeffrey S. Beis et David G. Lowe, « Shape indexing using approximate nearest-neighbour search in high-dimensional spaces », dans Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, Porto-Rico, (lire en ligne), p. 1000 - 1006.
- Lowe (2004), p. 110.
- Lowe (2004), p. 111.
- Lowe (2004), p. 112.
- Lowe (2004), p. 113.
- D.G. Lowe, « Local feature view clustering for 3D object recognition », IEEE Conference on Computer Vision and Pattern Recognition, Kauai, Hawaii, 2001, pp. 682-688.
- (en) K. Mikolajczyk et C. Schmid, « A performance evaluation of local descriptors », IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 27, no 10, , p. 1615–1630 (lire en ligne)
- (en) Johannes Bauer, Niko Sünderhauf et Peter Protzel, « Comparing several implementations of two recently published feature detectors », dans Proceedings of the International Conference on Intelligent and Autonomous Systems, Toulouse, (lire en ligne), p. 3.
- (en) Yan Cui, Nils Hasler, Thorsten Thormählen et Hans-Peter Seidel, « Scale invariant feature transform with irregular orientation histogram binning », dans Proceedings of the International Conference on Image Analysis and Recognition, Halifax (Canada), Springer, (lire en ligne).
- (en) Matthew Toews et William M. Wells III, « SIFT-Rank: ordinal descriptors for invariant feature correspondence », dans IEEE International Conference on Computer Vision and Pattern Recognition, (lire en ligne), p. 172–177.
- (en) Stephen Se, David Lowe et Jim Little, « Vision-based mobile robot localization and mapping using scale-invariant features », dans Proceedings of the IEEE International Conference on Robotics and Automation, vol. 2, (lire en ligne), p. 2051.
- (en) Stephen Se, David Lowe et Jim Little, « Vision-based mobile robot localization and mapping using scale-invariant features », dans Proceedings of the IEEE International Conference on Robotics and Automation, vol. 2, (lire en ligne), p. 2053.
- (en) M. Brown et David G. Lowe, « Recognising panoramas », dans Proceedings of the ninth IEEE International Conference on Computer Vision, vol. 2, (lire en ligne), p. 1218–1225.
- (en) Matthew Brown et David Lowe, « Automatic Panoramic Image Stitching using Invariant Features », International Journal of Computer Vision, vol. 74, no 1, , p. 59-73 (lire en ligne).
- (en) Iryna Gordon et David G. Lowe, « What and where: 3D object recognition with accurate pose », dans Toward Category-Level Object Recognition, Springer-Verlag, (lire en ligne), p. 67-82.
- (en) Ivan Laptev et Tony Lindeberg, « Local descriptors for spatio-temporal recognition », dans ECCV'04 Workshop on Spatial Coherence for Visual Motion Analysis, vol. 3667, Springer, (lire en ligne), p. 91–103.
- (en) Ivan Laptev, Barbara Caputo, Christian Schuldt et Tony Lindeberg, « Local velocity-adapted motion events for spatio-temporal recognition », Computer Vision and Image Understanding, vol. 108, , p. 207–229 (lire en ligne).
- (en) Paul Scovanner, Saad Ali et Mubarak Shah, « A 3-dimensional SIFT descriptor and its application to action recognition », dans Proceedings of the 15th International Conference on Multimedia, (ISBN 978-1-59593-702-5, lire en ligne), p. 357–360.
- (en) Juan Carlos Niebles, Hongcheng Wang et Li Fei-Fei1, « Unsupervised learning of human action categories using spatial-temporal words », dans Proceedings of the British Machine Vision Conference, Edinburgh, (lire en ligne).
- (en) Matthew Toews, William M. Wells III, D. Louis Collins et Tal Arbel, « Feature-based morphometry: discovering group-related anatomical patterns », NeuroImage, vol. 49, no 3, , p. 2318-2327 (lire en ligne).
- (en) Svetlana Lazebnik, Cordelia Schmid et Jean Ponce, « Semi-local affine parts for object recognition », dans Proceedings of the British Machine Vision Conference, (lire en ligne), p. 959-968.
- (en) Sungho Kim, Kuk-Jin Yoon et In So Kweon, « Object recognition using a generalized robust invariant feature and Gestalt’s law of proximity and similarity », dans Conference on Computer Vision and Pattern Recognition Workshop, New York, (ISBN 0-7695-2646-2, lire en ligne), p. 726-741.
- (en) Herbert Bay, Tinne Tuytelaars et Luc Van Gool, « SURF: Speeded Up Robust Features », dans Proceedings of the European Conference on Computer Vision (lire en ligne), p. 404-417.
- (en) Yan Ke et R. Sukthankar, « PCA-SIFT: A More Distinctive Representation for Local Image Descriptors », dans Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, vol. 2, (lire en ligne), p. 506-513.
- (en) Krystian Mikolajczyk et Cordelia Schmid, « A performance evaluation of local descriptors », IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 27, no 10, , p. 1615-1630 (lire en ligne).
- (en) Yan Ke et R. Sukthankar, « PCA-SIFT: A More Distinctive Representation for Local Image Descriptors », dans Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, vol. 2, (lire en ligne), p. 508.
- (en) Daniel Wagner, Gerhard Reitmayr, Alessandro Mulloni, Tom Drummond et Dieter Schmalstieg, « Pose tracking from natural features on mobile phones », dans 7th IEEE/ACM International Symposium on Mixed and Augmented Reality, (lire en ligne), p. 125-134.
- Wagner et al. (2008), p. 128.
- (en) Niels Henze, Torben Schinke et Susanne Boll, « What is That? Object Recognition from Natural Features on a Mobile Phone », dans Proceedings of the Workshop on Mobile Interaction with the Real World, (lire en ligne).
- Wagner et al. (2008), p. 133-134.
Annexes
Articles connexes
Publications
- (en) YuanBin Wang, Zhang Bin et Yu Ge, « The Invariant Relations of 3D to 2D Projection of Point Sets », Journal of Pattern Recognition Research, vol. 3, no 1, , p. 14-23 (lire en ligne)
- (en) David G. Lowe, « Distinctive Image Features from Scale-Invariant Keypoints », International Journal of Computer Vision, vol. 60, no 2, , p. 91-110 (lire en ligne)
- (en) Krystian Mikolajczyk et Cordelia Schmid, « A performance evaluation of local descriptors », IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 27, no 10, , p. 1615-1630 (lire en ligne)
- (en) Svetlana Lazebnik, Cordelia Schmid et Jean Ponce, « Semi-Local Affine Parts for Object Recognition », Proceedings of the British Machine Vision Conference, vol. 2, , p. 959-968 (lire en ligne)
Implémentations de SIFT
- (en) Rob Hess, « SIFT Library », (consulté le ).
- (en) David G. Lowe, « Demo Software: SIFT Keypoint Detector », (consulté le ).
- (en) Yan Ke et Rahul Sukthankar, « PCA-SIFT: A More Distinctive Representation for Local Image Descriptors », (consulté le ).
- (en) Jean-Michel Morel et Guoshen Yu, « ASIFT: A New Framework for Fully Affine Invariant Comparison », (ISSN 2105-1232, consulté le ).
- (en) Andrea Vedaldi et Brian Fulkerson, « VLFeat.org », (consulté le ).
- (en) Wan-Lei Zhao, « Lip-vireo », (consulté le ).
- Depuis sa version 2.2 (), OpenCV intègre une implémentation de SIFT.







































![[x y]^{\rm T}](https://img.franco.wiki/i/1950ddf2ef30ababa5ce15b67823889b047c9bbd.svg)
![[u v]^{\rm T}](https://img.franco.wiki/i/8358c238fe01f7c18bcafa2b75f7cdac868e9f51.svg)

![[t_x t_y]^{\rm T}](https://img.franco.wiki/i/445da26c424927b4adc97072ad6afe59f58ed0c9.svg)




















