RANSAC

Un exemple simple est l'ajustement d'une ligne située dans un plan (2D) à une série d'observations. On suppose que cet ensemble contient à la fois des points pertinents (inliers), c'est-à-dire, les points qui peuvent être approximativement ajustés à une ligne, et des points aberrants (outliers), les points qui sont éloignés de ce modèle de ligne. Un simple traitement par une méthode des moindres carrés donnera une ligne qui est mal ajustée aux points pertinents. En effet, la droite s'ajustera de manière optimale à tous les points, y compris les points aberrants[2]. La méthode RANSAC, par contre, peut générer un modèle qui ne tiendra compte que des points pertinents, à condition que la probabilité, lorsqu'on tire des points au hasard, de ne sélectionner que des points pertinents, soit suffisamment élevée. Cependant, il n'y a aucune garantie d'obtenir cette situation, et il existe un certain nombre de paramètres de l'algorithme qui doivent être soigneusement choisis pour maintenir ce niveau de probabilité suffisamment élevé.

• 
  Un jeu de données avec de nombreuses valeurs aberrantes pour lesquelles une ligne doit être ajustée.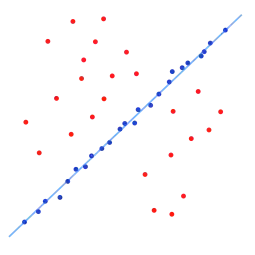
• 
  Ligne ajustée avec la méthode RANSAC, les valeurs aberrantes n'ont aucune influence sur le résultat.

Les données d'entrée de l'algorithme RANSAC sont un ensemble de valeurs des données observées, un modèle paramétré qui peut expliquer ou être ajusté aux observations, et des paramètres d'intervalle de confiance.

RANSAC atteint son objectif en sélectionnant itérativement un sous-ensemble aléatoire des données d'origine. Ces données sont d'hypothétiques données pertinentes et cette hypothèse est ensuite testée comme suit :

1. Un modèle est ajusté aux données pertinentes hypothétiques, c'est-à-dire que tous les paramètres libres du modèle sont estimés à partir de ce sous-ensemble de données ;
2. Toutes les autres données sont ensuite testées sur le modèle précédemment estimé. Si un point correspond bien au modèle estimé, alors il est considéré comme une donnée pertinente candidate ;
3. Le modèle estimé est considéré comme correct si suffisamment de points ont été classés comme données pertinentes candidates ;
4. Le modèle est ré-estimé à partir de ce sous-ensemble des données pertinentes candidates ;
5. Finalement, le modèle est évalué par une estimation de l'erreur des données pertinentes par rapport au modèle.

Cette procédure est répétée un nombre fixe de fois, chaque fois produisant soit un modèle qui est rejeté parce que trop peu de points sont classés comme données pertinentes, soit un modèle réajusté et une mesure d'erreur correspondante. Dans ce dernier cas, on conserve le modèle réévalué si son erreur est plus faible que le modèle précédent.

L'algorithme RANSAC générique, en pseudocode, fonctionne comme suit :

entrées :
    data - un ensemble d'observations
    modele - un modèle qui peut être ajusté à des données
    n - le nombre minimum de données nécessaires pour ajuster le modèle
    k - le nombre maximal d'itérations de l'algorithme
    t - une valeur seuil pour déterminer si une donnée correspond à un modèle
    d - le nombre de données proches des valeurs nécessaires pour faire valoir que le modèle correspond bien aux données

sorties :
    meilleur_modèle - les paramètres du modèle qui correspondent le mieux aux données (ou zéro si aucun bon modèle n'a été trouvé)
    meilleur_ensemble_points - données à partir desquelles ce modèle a été estimé
    meilleure_erreur - l'erreur de ce modèle par rapport aux données
itérateur := 0
meilleur_modèle := aucun
meilleur_ensemble_points := aucun
meilleure_erreur := infini
tant que itérateur < k
    points_aléatoires := n valeurs choisies au hasard à partir des données
    modèle_possible := paramètres du modèle correspondant aux points_aléatoires
    ensemble_points := points_aléatoires
    Pour chaque point des données pas dans points_aléatoires
        si le point s'ajuste au modèle_possible avec une erreur inférieure à t
            Ajouter un point à ensemble_points
    si le nombre d'éléments dans ensemble_points est > d
        (ce qui implique que nous avons peut-être trouvé un bon modèle,
        on teste maintenant dans quelle mesure il est correct)
        modèle_possible := paramètres du modèle réajusté à tous les points de ensemble_points
        erreur := une mesure de la manière dont ces points correspondent au modèle_possible
        si erreur < meilleure_erreur
            (nous avons trouvé un modèle qui est mieux que tous les précédents,
            le garder jusqu'à ce qu'un meilleur soit trouvé)
            meilleur_modèle := modèle_possible
            meilleur_ensemble_points := ensemble_points
            meilleure_erreur := erreur
    incrémentation de l’itérateur
retourne meilleur_modèle, meilleur_ensemble_points, meilleure_erreur

Variantes possibles de l'algorithme RANSAC :

• arrêter la boucle principale si un modèle assez bon a été trouvé, c'est-à-dire avec une erreur suffisamment petite ; cette solution peut épargner du temps de calcul, au détriment d'un paramètre supplémentaire ;
• calculer erreur directement à partir de modèle_possible, sans ré-estimation du modèle à partir de ensemble_points ; cette solution peut faire gagner du temps au détriment de la comparaison des erreurs liées à des modèles qui sont estimés à partir d'un petit nombre de points et donc plus sensibles au bruit.

Les valeurs des paramètres t et d doivent être fixées conformément aux exigences spécifiques liées à l'application et à l'ensemble de données. qui peuvent être éventuellement fondées sur l'évaluation expérimentale. Le paramètre k (le nombre d'itérations), cependant, peut être déterminé à partir d'un résultat théorique. Soit p la probabilité que l'algorithme RANSAC pendant une itération sélectionne uniquement des données pertinentes dans l'ensemble des données d'entrées, lorsqu'il choisit les n points à partir desquels les paramètres du modèle seront estimés. Lorsque cela se produit, le modèle qui en résulte est susceptible d'être pertinent, donc p donne la probabilité que l'algorithme produise un résultat correct. Soit w, la probabilité de choisir un point pertinent à chaque fois qu'un seul point est sélectionné, c'est-à-dire

w = nombre de points pertinents dans les données / nombre de points dans les données

Il est fréquent que w ne soit pas connu à l'avance, mais que l'on puisse en estimer une valeur approximative. En supposant que les n points nécessaires pour l'estimation d'un modèle sont sélectionnées de manière indépendante, wⁿ est la probabilité que l'ensemble des n points correspond à des points pertinents et 1 - wⁿ est la probabilité qu'au moins un des n points soit un cas aberrant, un cas qui implique qu'un mauvais modèle sera estimé à partir de cet ensemble de points. Cette probabilité à la puissance de k est la probabilité que l'algorithme ne choisisse jamais un ensemble de n points qui seraient tous pertinents et cela doit être égale à 1 - p. Par conséquent,

${\displaystyle 1-p=(1-w^{n})^{k}}$

qui, en prenant le logarithme des deux côtés, conduit à

${\displaystyle k={\frac {\log(1-p)}{\log(1-w^{n})}}}$

Il convient de noter que ce résultat suppose que les n points de données sont sélectionnés de façon indépendante, c'est-à-dire, qu'un point qui a été sélectionné une fois est remis et peut être sélectionné à nouveau dans la même itération. Cela n'est pas souvent une approche pertinente et la valeur calculée pour k devrait être prise comme une limite supérieure dans le cas où les points sont choisis sans remise. Par exemple, dans le cas de la recherche d'une ligne qui s'ajuste à la série de données illustrée sur la figure ci-dessus, l'algorithme RANSAC choisit généralement deux points à chaque itération et calcule le modèle_possible comme la ligne qui relie ces deux points et il est alors important que les deux points soient distincts.

Pour gagner en qualité, l'écart type ou des multiples de celui-ci peuvent être ajouté à ${\displaystyle k}$. L'écart type de ${\displaystyle k}$ est défini comme

${\displaystyle \mathrm {SD} (k)={\frac {\sqrt {1-w^{n}}}{w^{n}}}}$

Un avantage de RANSAC est sa capacité à calculer de manière robuste les paramètres du modèle, c'est-à-dire qu'il peut estimer les paramètres avec un degré élevé de précision, même si une quantité importante de valeurs aberrantes (outliers) est présente dans les données. Un inconvénient de RANSAC est qu'il n'y a pas de limite supérieure sur le temps de calcul de ces paramètres. Lorsqu'une limite est utilisée (un nombre maximal d'itérations), la solution obtenue peut ne pas être la solution optimale. Un autre inconvénient de RANSAC est qu'elle suppose de fixer des seuils spécifiques au problème traité.

RANSAC ne peut estimer qu'un seul modèle à un ensemble de données particulier. Comme pour toute approche à modèle unique, lorsque deux (ou plusieurs) modèles coexistent, RANSAC peut ne parvenir à trouver ni l'un ni l'autre.

L'algorithme RANSAC est souvent utilisé dans le domaine de la vision par ordinateur, par exemple, pour résoudre simultanément les problèmes de mise en correspondance et d'estimer la matrice fondamentale liée à une paire stéréo de caméras.

• (en) David A. Forsyth and Jean Ponce, Computer Vision, a modern approach, Upper Saddle River NJ, Prentice Hall, 2003, 693 p., poche (ISBN 978-0-13-085198-7, LCCN 2002726601)
• (en) Richard Hartley et Andrew Zisserman, Multiple View Geometry in Computer Vision, Cambridge University Press, 2003, 2^e éd.
• (en) P.H.S. Torr, and D.W. Murray, « The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix », International Journal of Computer Vision, vol. 24,‎ 1997, p. 271–300 (DOI 10.1023/A:1007927408552)
• (en) Ondrej Chum, « Two-View Geometry Estimation by Random Sample and Consensus », PhD Thesis,‎ 2005 (lire en ligne)

• (en) RANSAC Toolbox for MATLAB. Boite à outil MATLAB.
• (en) [PDF] « RANSAC for Dummies » (version du 3 avril 2015 sur Internet Archive) : un tutoriel utilisant la boite à outil RANSAC pour MATLAB.
• (en) ransac.py Implémentation en Python.
• (en) Scikit-image et Scikit-learn contiennent une implémentation en Python.
• (en) [PDF] 25 Years of RANSAC Workshop