Résistance thermique

La résistance thermique $R_{\mathrm {th} }$ quantifie l'opposition à un flux thermique entre deux isothermes entre lesquels s'effectue un transfert thermique de sorte que :

R_{\mathrm {th} }={\frac {\Delta T}{\Phi }}

où $\Phi$ est le flux thermique en watts (W) et $\Delta T$ est la différence de température en kelvins (K). La résistance thermique s'exprime en kelvins par watt (K/W). La résistance thermique surfacique $r_{\mathrm {th} }$ (en mètres carrés-kelvins par watt, K·m²·W^-1, est son équivalent rapporté à la densité de flux thermique $\varphi$ (en watts par mètre carré, W/m²) :

r_{\mathrm {th} }={\frac {\Delta T}{\varphi }}={\frac {\Delta T\,S}{\Phi }}=R_{\mathrm {th} }\,S

Cette dernière est davantage utilisée dans le cas des surfaces planes notamment dans le domaine de la thermique du bâtiment.

L'inverse de la résistance thermique $1/R_{\mathrm {th} }$ est la conductance thermique ou coefficient de transmission thermique. L'inverse de la résistance thermique surfacique $1/r_{\mathrm {th} }$ est le coefficient de transmission thermique surfacique (en watts par mètre carré-kelvin, W·m^-2·K^-1).

Selon le mode de transfert thermique, on distingue :

la résistance thermique de conduction, pour un flux thermique par conduction ;
la résistance thermique de convection, pour un flux thermique par convection.

Résistance thermique de conduction

Surface plane

Les isothermes sont des surfaces planes et parallèles, c'est par exemple le cas d'un mur d'un bâtiment. La résistance thermique de conduction $R_{\mathrm {th\,cond} }$ d’un élément d’épaisseur $e$ en mètres (m), de surface $S$ en mètres carrés (m²), et de conductivité thermique $\lambda$ [alpha 1] en watts par mètre-kelvin[1] (W m^-1 K^-1) s'exprime[2] :

R_{\mathrm {pla} }={\frac {e}{\lambda \ S}}\,

Cette formule néglige les effets de bord en supposant que les dimensions (longueur, largeur) de l’élément sont très grandes devant son épaisseur ( $L\gg e$ et $l\gg e$ ). On suppose aussi que les matériaux constituant l’élément sont isotropes, c’est-à-dire que leur comportement thermique est le même quelle que soit la direction. L’élément peut être constitué de différents matériaux isotropes (ou considérés comme tels), par exemple un mur en brique recouvert d’un enduit à l’extérieur et d’un isolant à l’intérieur. On trouve aussi la relation de résistance thermique surfacique[3] :

r_{\mathrm {pla} }={\frac {e}{\lambda }}\,

Démonstration

En partant de l'équation de la chaleur, bilan de puissance local : $\rho \,c_{p}{\frac {\partial T}{\partial t}}=-\mathrm {div} \,{\overrightarrow {\varphi }}+{\dot {E}}_{\mathrm {prod} }$ .

En régime permanent ${\frac {\partial T}{\partial t}}=0$ .
En l'absence de source interne de chaleur : ${\dot {E}}_{\mathrm {prod} }=0$ .
En supposant que $\lambda$ est constante sur toute l'épaisseur de la paroi.
En considérant que le transfert thermique ne s'effectue que par conduction.
En considérant que les dimensions de la surface sont grandes devant l'épaisseur, l'étude peut se faire en monodimensionnel. La densité de flux est constante dans le sens de l'épaisseur, sens qui oriente l'axe des $x$ . Le flux dans les directions de $y$ et de $z$ sont nuls.

L'équation de la chaleur devient : $\mathrm {div} {\overrightarrow {\varphi }}={\frac {\mathrm {d} \varphi _{x}}{\mathrm {d} x}}=0\Leftrightarrow \varphi _{x}=-\lambda {\frac {\mathrm {d} T}{\mathrm {d} x}}=\mathrm {cte}$ .

La température évolue linéairement : $T(x)=-{\frac {\varphi _{x}}{\lambda }}x+K$ .

Alors $\Delta T={\frac {\varphi _{x}}{\lambda }}e\Leftrightarrow r_{\mathrm {th} }={\frac {\Delta T}{\varphi _{x}}}={\frac {e}{\lambda }}$ .

Surface cylindrique

Les isothermes sont des cylindres concentriques, c'est par exemple le cas d’un tuyau, d’une canalisation, etc. La résistance thermique de conduction $R$ d’un élément cylindrique de longueur $L$ en mètres (m), de rayon interne $r_{1}$ et externe $r_{2}$ en mètres (m) vaut[2] :

R_{cyl}={\frac {\ln({r_{2}/r_{1}})}{2\pi \lambda L}}

Démonstration

Si on reprend la démonstration précédente, seule la géométrie change : on effectue l'étude en coordonnées cylindriques. Les flux dans les directions ${\overrightarrow {e_{z}}}$ et ${\overrightarrow {e_{\theta }}}$ sont nuls. L'équation de la chaleur devient : $\mathrm {div} {\overrightarrow {\varphi }}={\frac {1}{r}}{\frac {\mathrm {d} \left(r\,\varphi _{r}\right)}{\mathrm {d} r}}=0$ .

La loi Fourier donne : ${\overrightarrow {\varphi }}_{r}=-\lambda \ {\overrightarrow {\mathrm {grad} }}\,T=-\lambda {\frac {\mathrm {d} T}{\mathrm {d} r}}{\overrightarrow {e_{r}}}$ .

On en déduit que : ${\frac {\mathrm {d} }{\mathrm {d} r}}\left(r\,{\frac {\mathrm {d} T}{\mathrm {d} r}}\right)=0\Leftrightarrow r\,{\frac {\mathrm {d} T}{\mathrm {d} r}}=K\Leftrightarrow \mathrm {d} T=K{\frac {\mathrm {d} r}{r}}$ .

D'où : $T(r)=K\ln r+K'$ .

Ce qui permet d'écrire que : $\Delta T=T_{1}-T_{2}=K\ln {\frac {r_{1}}{r_{2}}}$ .

L'expression du flux élémentaire est : $\mathrm {d} \Phi =-\lambda \ {\overrightarrow {\mathrm {grad} }}\,T\cdot {\overrightarrow {\mathrm {dS} }}=-\lambda {\frac {\mathrm {d} T}{\mathrm {d} r}}r\,\mathrm {d} \theta \,\mathrm {d} z$ .

Le flux thermique pour un longueur de tube $L$ et pour une section de rayon $r$ est : $\Phi =-\lambda \,K\,2\pi \,L=-{\frac {\lambda \,2\pi \,L}{\ln {\frac {r_{1}}{r_{2}}}}}\Delta T={\frac {\Delta T}{R_{\mathrm {th} }}}$ .

Alors $R_{cyl}={\frac {\ln({r_{2}/r_{1}})}{2\pi \lambda L}}$ .

Surface sphérique

Si les isothermes sont des sphères concentriques, de rayon interne $r_{1}$ et externe $r_{2}$ [2] en mètres (m), la résistance thermique s'exprime :

R_{sph}={\frac {1}{4\pi \lambda }}\left({\frac {1}{r_{1}}}-{\frac {1}{r_{2}}}\right)

Démonstration

Si on reprend la démonstration précédente, seule la géométrie change : on effectue l'étude en coordonnées sphériques. Les flux dans les directions ${\overrightarrow {e_{\phi }}}$ et ${\overrightarrow {e_{\theta }}}$ sont nuls. L'équation de la chaleur devient : $\mathrm {div} {\overrightarrow {\varphi }}={\frac {1}{r^{2}}}{\frac {\mathrm {d} \left(r^{2}\,\varphi _{r}\right)}{\mathrm {d} r}}=0$ .

La loi Fourier donne : ${\overrightarrow {\varphi }}_{r}=-\lambda \ {\overrightarrow {\mathrm {grad} }}\,T=-\lambda {\frac {\mathrm {d} T}{\mathrm {d} r}}{\overrightarrow {e_{r}}}$ .

On en déduit que : ${\frac {\mathrm {d} }{\mathrm {d} r}}\left(r^{2}\,{\frac {\mathrm {d} T}{\mathrm {d} r}}\right)=0\Leftrightarrow r^{2}\,{\frac {\mathrm {d} T}{\mathrm {d} r}}=K\Leftrightarrow \mathrm {d} T=K{\frac {\mathrm {d} r}{r^{2}}}$ .

D'où : $T(r)=-{\frac {K}{r}}+K'$ .

Ce qui permet d'écrire que : $\Delta T=T_{1}-T_{2}=K\left({\frac {1}{r_{2}}}-{\frac {1}{r_{1}}}\right)$ .

Le flux thermique sur la sphère ( $\theta \in [0,\pi ]$ et $\phi \in [0,2\pi ]$ ) est : $\Phi =-\lambda \,K\,4\pi =-{\frac {\lambda \,4\pi }{{\frac {1}{r_{2}}}-{\frac {1}{r_{1}}}}}\Delta T={\frac {\Delta T}{R_{\mathrm {th} }}}$ .

Alors $R_{\mathrm {sph} }={\frac {1}{4\pi \lambda }}\left({\frac {1}{r_{1}}}-{\frac {1}{r_{2}}}\right)$ .

Résistance thermique de convection

La résistance thermique de convection entre une paroi et le fluide à grande distance de la paroi, pour une surface d'échange ${S}$ en mètres carrés (m²) s'exprime :

R_{\mathrm {cv} }={\frac {1}{h\ S}}

La résistance thermique surfacique est simplement l'inverse du coefficient de convection thermique ${h}$ en watts par mètre carré-kelvin (W m^-2 K^-1) :

r_{\mathrm {cv} }={\frac {1}{h}}

Contrairement à la résistance thermique de conduction, celle-ci ne dépend pas de l’épaisseur de la paroi considérée.

La résistance thermique de convection dépend, tout comme le coefficient de convection, de la surface (géométrie, rugosité, orientation), des propriétés du fluide (masse volumique, capacité thermique massique, viscosité, conductivité thermique) et du régime d'écoulement (laminaire, turbulent ou mixte).

Associations de résistances thermiques

Résistances thermiques en série

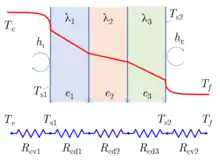
Cas d'une paroi constituée de trois couches différentes.

Généralement, une paroi est entourée de fluides de part et d'autre. Des phénomènes de convection se produisent sur chacune de ses faces et un phénomène de conduction est responsable du transfert thermique à travers la paroi. Cette dernière peut être constituées de plusieurs couches comme sur l'illustration ci-contre. Chacun de ses phénomènes donne lieu à une résistance thermique qui peut être mise en série, par analogie avec les résistances électriques[4]. Les différentes résistances thermiques sont dans ce cas en séries, la résistance thermique totale est la somme des résistances thermiques. On suppose que ces températures et les coefficient de convection thermique $h_{i}$ et $h_{e}$ afférents aux fluides sont constants et uniforme par rapport aux surfaces de contact[5].

R_{\mathrm {th} }={\frac {1}{h_{i}S}}+{\frac {e_{1}}{\lambda _{1}S}}+{\frac {e_{2}}{\lambda _{2}S}}+{\frac {e_{3}}{\lambda _{3}S}}+{\frac {1}{h_{e}S}}

{\Phi }={\frac {T_{c}-T_{f}}{R_{\mathrm {th} }}}

Résistances thermiques en parallèle

Résistances thermiques en parallèle

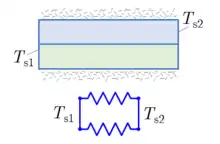
Dans le cas d'une paroi composite constituée de plusieurs matériaux dont les températures de surfaces sont les mêmes, on peut considérer, toujours par analogie avec les résistances électriques, une association de résistances en parallèle[6]. $R_{\mathrm {th1} }$ et $R_{\mathrm {th2} }$ étant les résistances de chacune des parois individuellement, la résistance de l'ensemble vaut :

R_{\mathrm {th} }={\frac {R_{\mathrm {th1} }\,R_{\mathrm {th2} }}{R_{\mathrm {th1} }+R_{\mathrm {th2} }}}

Applications

En électronique

Les éléments semi-conducteurs de puissance sont généralement montés sur des dissipateurs thermiques (ou refroidisseurs) destinés à favoriser l’évacuation de l’énergie produite au niveau des jonctions anode-cathode pour les diodes, les thyristors, les triacs, et les GTO ou collecteur-émetteur pour les transistors bipolaires et les IGBT, ou drain-source pour les MOSFET. Dans ce cas, la résistance thermique entre la jonction et l'air ambiant est une somme de trois résistances thermiques :

Résistance thermique jonction-boîtier

Elle est donnée dans les feuilles de caractéristiques du constructeur. Voici quelques ordres de grandeur de résistances thermiques selon les types de boîtiers courants :

petits boîtiers cylindriques, plastiques ou métalliques (TO-39 / TO-5, TO-92, TO-18) : entre 20 et 175 K/W[7] - [8] - [9] - [10] ;
boîtiers intermédiaires plats, plastiques (TO-220[11], TO-126/SOT-32[12]) : entre 0,6 et 6 K/W ;
boîtiers moyens de composants de puissance, plastiques ou métalliques (ISOTOP[13], TO-247[14], TOP-3, TO-3[15]) : de 0,2 à 2 K/W ;
boîtiers de composants modulaires de puissance : de 0,01 à 0,5 K/W[16] - [17] - [18] - [19] - [20] - [21].

Le transfert thermique entre la jonction et le boîtier se fait essentiellement par conduction.

Résistance thermique boîtier-dissipateur thermique

Elle dépend de la surface de contact entre l'élément et le dissipateur et de la présence ou non d'un isolant électrique. Le transfert thermique entre le boîtier et le dissipateur se fait essentiellement par conduction. Par exemple pour un boîtier TO-3 : sans isolant, à sec : 0,25 K/W[22] ; sans isolant, avec graisse au silicone : 0,15 K/W[22] ; avec isolant mica 50 µm et graisse au silicone : 0,35 K/W[23].

Résistance thermique dissipateur thermique-ambiance

Le transfert thermique entre le dissipateur et l'air ambiant se fait essentiellement par convection : l'air ambiant vient lécher le dissipateur ; l'air chauffé à son contact s'élève, il est remplacé par de l'air plus froid et ainsi de suite. La résistance thermique dépend de la surface du dissipateur, de son type (plat, à ailettes, etc.), de son orientation (les parties verticales dissipent mieux les calories que les parties horizontales), de sa couleur (le noir rayonne plus que le brillant). Elle peut être diminuée en forçant une circulation d'air (comme dans les ordinateurs personnels) ou en faisant circuler de l'eau dans des tuyaux prévus à cet effet. La résistance thermique est donnée par le constructeur.

Dans le bâtiment

Dans le cas d'un transfert thermique à travers un mur les valeurs $R_{cv}$ de convection ne prennent pas en compte les apports de chaleurs par rayonnement. Les textes officiels donnent des valeurs de résistance thermique d'échange superficielle interne et externe ( $R_{si}$ et $R_{se}$ ) qui tiennent compte des phénomènes de convection et de rayonnement[24].

La résistance thermique des matériaux est parfois utilisée dans les règlementations thermiques, telles que la RT 2005 et RT 2020 en France. Cependant cette grandeur est petit à petit abandonnée au profit du coefficient de transfert thermique U, qui prend aussi en compte la mise en œuvre du produit.

Notes et références

La conductivité thermique est parfois notée k (communauté anglophone).

Michel Dubesset, Le manuel du Système International d'unités - Lexique et conversions, éd. Technip, 2000, 169 p. (ISBN 2710807629 et 978-2710807629), p. 124 [lire en ligne (page consultée le 16 décembre 2012)].
[PDF] Frédéric Doumenc, Éléments de thermodynamique et thermique – II, Thermique, université Pierre et Marie Curie, année 2009/2010, sur le site fast.u-psud.fr, consulté le 16 juin 2012, p. 20-21.
Michel Dubesset, Le manuel du Système International d'unités - Lexique et conversions, éd. Technip, 2000, 169 p. (ISBN 2710807629 et 978-2710807629), p. 108 [lire en ligne (page consultée le 16 décembre 2012)].
Jean-Luc Battaglia, Andrzej Kusiak et Jean-Rodolphe Puiggali 2010, p. 56
Ana-Maria Bianchi, Yves Fautrelle, Jacqueline Etay. Transferts thermiques. PPUR presses polytechniques, 2004. Consulter en ligne
Theodore L. Bergman et al. 2011, p. 120
(en) [PDF] STMicroelectronics, 2N3439 – 2N3440, « Silicon NPN Transistors », 2000, p. 2/4
(en) [PDF] Diodes Incorporated/Zetex Semiconductors, ZTX851, « NPN Silicon planar Medium Power Hight Current Transistor », Issue-2, août 1994, p. 3-295
(en) [PDF] On Semiconductor, MPSA92, MPSA93, « Hight Voltage Transistor, PNP Silicon », octobre 2005, p. 1
(en) [PDF] Philips Semiconductors, « 2N2222; 2N2222A, NPN switching transistor », 29 mai 1997
(en) [PDF] International Rectifier, « Automotive Mosfet, IRFZ 1405Z », 22 juillet 2005, p. 1,
(en) [PDF] STMicroelectronics, « MJE340 – MJE350, Complementary Silicon Power Transistors », 2003, p. 2/5
(en) [PDF] STMicroelectronics, « STE70NM60 », mars 2003, p. 2/8
(en) [PDF] International Rectifier, « Insulated Gate Bipolar Transistor, IRG4PC40S », 30 décembre 2000, p. 1
(en) [PDF] STMicroelectronics, « 2N3055 – MJ2955, Complementary Silicon Power Transistors », août 1999, p. 2/4
(en) [PDF] ABB, « ABB HiPack, IGBT Module 5SNA 1600N170100 », octobre 2006, p. 3/9
(en) (de) [PDF] Infineon/Eupec, « IGBT Module, FD 400 R65 KF1-K » « Copie archivée » (version du 8 novembre 2018 sur Internet Archive)
(en) [PDF] Fuji electric, « 2-Pack IGBT, 2MBI 600NT-060 »
(en) [PDF] Mitsubishi Electric, « Mutsubishi IGBT Modules, CM200DU-12H »
(en) [PDF] Ixys, « IGBT Module, MII/MID/MDI400-12E4 », 2007
(en) [PDF] Fairchild Semiconductor, « IGBT, FMG2G50US60 », septembre 2001
Transistors de puissance, Thomson CSF - Sescosem, 1975, p. 77
Transistors de puissance, op. cit., p. 81
Résistance thermique d’échange superficiel et La résistance thermique d'échange superficiel (Rsi et Rse) sur le site energieplus-lesite.be de Architecture et Climat de l'UCL

Bibliographie

Jean-François Sacadura, Initiation aux transferts thermiques, Lavoisier, Paris, 1993 (ISBN 2-85206-618-1)

Jean-Luc Battaglia, Andrzej Kusiak et Jean-Rodolphe Puiggali, Introduction aux transferts thermiques : Cours et exercices corrigés, Paris, Dunod, 2010 (ISBN 978-2-10-054828-6)

(en) Theodore L. Bergman, Adrienne S. Lavine, Franck P. Incropera et David P. Dewitt, Fundamentals of heat and Mass transfer, John Wiley & Sons, 2011, 7^e éd. (ISBN 978-0470-50197-9)

Voir aussi

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.