Réseau de tri
En Informatique, un réseau de tri est un algorithme de tri qui trie un nombre fixe de valeurs en utilisant une suite fixe de comparateurs. On peut voir un réseau de tri comme un réseau composé de fils et de comparateurs. Les valeurs, prises dans un ensemble ordonné, circulent le long des fils. Chaque comparateur connecte deux fils, compare les données qui entrent par les fils et les trie, sortant la plus petite donnée sur l'un des fils, la plus grande sur l’autre.
Les réseaux de tri diffèrent des algorithmes de tri par comparaison dans le sens où ils ne sont pas capables de traiter un nombre arbitraire d'entrées ; de plus, leur séquence de comparaisons est définie à l'avance, et indépendante du résultat des comparaisons précédentes. L'indépendance des séquences de comparaison est utile pour l'exécution en parallèle et pour la réalisation en hardware. Elle peut aussi être vue comme une protection contre un logiciel malveillant qui chercherait à examiner la nature des séquences triées.
Introduction
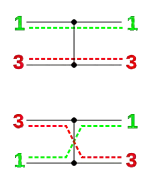
Un réseau de tri est constitué de deux types d'objets : les fils et les comparateurs. Les fils transportent des données de gauche à droite, les valeurs transportées, une par fil, traversent le réseau toutes en même temps et de façon synchrone. Chaque comparateur relie deux fils. Quand une paire de valeurs, transportée par une paire de fils, rencontre un comparateur, le comparateur échange les valeurs si et seulement si la valeur sur le fil supérieur est plus grande que la valeur sur le fil inférieur ; de la sorte, à la sortie c'est toujours la plus petite valeur qui se trouve sur le fil supérieur et la plus grande sur le fil inférieur. Voir le mode opératoire sur la figure ci-contre.
Formellement, si le fil supérieur contient x et le fil inférieur y, alors après avoir touché un comparateur les fils portent et respectivement, de sorte que la paire de valeur est triée[1]:p. 682. Un réseau composé de fils et de comparateurs est un réseau de comparateurs. Un réseau de comparateurs qui trie correctement toutes les entrées possibles dans l'ordre croissant est appelé un réseau de tri.
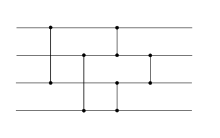
Le schéma ci-dessous montre un réseau de comparateurs. Il est facile de voir pourquoi ce réseau trie correctement les entrées : les quatre premiers comparateurs font descendre la plus grande valeur vers le fil du bas et font remonter la plus petite valeur vers le fil du haut. Le comparateur final trie simplement les valeurs des deux fils du milieu. C'est donc un réseau de tri.

Profondeur et taille
L'efficacité d'un réseau de tri peut être mesurée par sa taille totale, c'est-à-dire le nombre de comparateurs utilisés, ou par sa profondeur , définie comme étant le plus grand nombre de comparateurs qu'une valeur d'entrée peut rencontrer sur son chemin à travers le réseau. Le réseau peut effectuer certaines comparaisons en parallèle, représentées dans la notation graphique par des comparateurs qui se trouvent sur la même ligne verticale. En supposant que toutes les comparaisons prennent la même unité de temps, la profondeur du réseau est égale au nombre d'unités de temps requis pour l'exécuter en parallèle[1]:p. 683-684 - [2].
Réseaux de tri par insertion et par sélection
On construit facilement un réseau de tri de taille arbitraire récursivement en utilisant le principe à la base du tri par insertion ou celui du tri par sélection. En supposant l'existence d'un réseau de tri de la taille n , on construit un réseau de taille n + 1 par « insertion » d'une donnée supplémentaire dans le sous-réseau déjà trié en utilisant le principe du tri par insertion. Pour cela, on ajoute au réseau une suite de comparateurs qui insère cette dernière valeur à sa place. On peut également opérer en utilisant le principe du tri à bulles : on débute par la « sélection » de la valeur la plus grande parmi les entrées, à l'aide d'une suite de comparateurs qui descend la plus grande valeur vers le bas, puis on continue par le tri récursif des valeurs restantes.
 Un réseau de tri qui trie d'abord les n premières valeurs, puis insère la valeur restante (tri par insertion). |
 Un réseau de tri qui descend d'abord la plus grande valeur vers le bas, puis trie les autres valeurs (tri à bulles). |
Ces deux réseaux de tri, même s'ils sont construits selon des principes algorithmiques différent, ont des structures similaires en tant que réseaux. Lorsqu'on aligne les comparateurs qui peuvent opérer en parallèle, on s'aperçoit qu'en fait ils sont identiques[3].
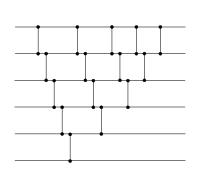 tri à bulles. |
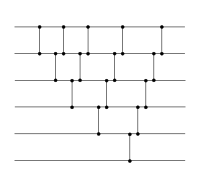 tri par insertion. |
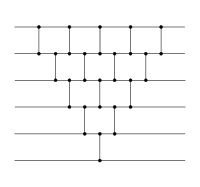 En alignant les comparateurs parallèles, les deux réseaux sont identiques. |
Ces réseaux de tri - par insertion ou par sélection - ont une profondeur 2n - 3[3], ce qui les rend trop longs en pratique. Il existe de meilleures constructions, présentées plus loin, dont la profondeur est logarithmique en n.
Principe du zéro-un
Le principe du zéro-un est une propriété utile pour démontrer qu'un réseau trie correctement les données. Alors qu'il est facile de prouver la validité de réseaux de tri dans certains cas particuliers, comme les réseaux par insertion ou par bulles, la preuve n'est pas toujours aussi facile. Il y a n! permutations de nombres dans un réseau à n fils, et tester tous les cas prend un temps considérable dès que n est grand Le nombre de cas à tester peut être réduit de manière significative, à 2n, en utilisant ce qu'on appelle le principe du zéro-un. Même s'il est toujours exponentiel, 2n est plus petit que n! pour n≥ 4, et la différence croît rapidement avec n.
Le principe du zéro-un stipule que si un réseau de tri trie correctement les 2n suites composées uniquement de zéros et de uns, alors il trie correctement toute suite d'entrées.
Ce principe non seulement réduit de façon drastique le nombre de test nécessaires pour garantir la validité d'un réseau; il est également d'une grande utilité pour la construction de réseaux de tri.
Démonstration. On constate d'abord le fait suivant sur les comparateurs : si une fonction monotone croissante est appliquée aux entrées, c'est-à-dire si et sont remplacés par et , alors le comparateur produit et . En raisonnant par récurrence sur la profondeur du réseau, ce résultat est étendu en un lemme stipulant que si un réseau transforme une suite en , alors il transforme en .
Supposons maintenant, en raisonnant par l’absurde, que le réseau trie les séquences formées de zéros et de uns, mais qu’il existe une séquence de nombres que le réseau ne trie pas correctement. Alors il existe des entrées avec que le réseau échange à la sortie. On définit une fonction monotone croissante particulière par
Puisque le réseau place avant , le lemme dit qu'il place avant dans la séquence de sortie pour l'entrée . Mais comme et , le réseau ne trie pas correctement la séquence zéro-un , en contradiction avec l'hypothèse de départ[1]:p. 686–688. Ceci prouve le principe du zéro-un.
Construction de réseaux de tri
Malgré leur simplicité, la théorie des réseaux de tri est étonnamment profonde et complexe. Les réseaux de tri ont été étudiés pour la première fois vers 1954 par Armstrong, Nelson et O'Connor[3] qui ensuite ont déposé un brevet pour ce concept[4].
Les réseaux de tri peuvent être employés soit en matériel soit en logiciel. Donald Knuth décrit la réalisation d'un comparateur d'entiers binaires par un dispositif électronique simple à trois états[3]. En 1968, Ken Batcher suggère leur emploi pour la construction de réseaux de commutation pour un ordinateur qui remplacerait à la fois les bus informatiques et les interrupteurs plus rapides mais plus coûteux[5]. Depuis les années 2000, les réseaux de tri, et particulièrement le tri par fusion bitonique, sont utilisés par la communauté GPGPU pour la construction d'algorithmes de tri qui tournent dans le processeur graphique[6].
Il existe plusieurs algorithmes pour construire des réseaux de tri simples et efficaces de profondeur O(log2 n) et de taille O(n log2 n). Parmi eux, il y a notamment[2]
- le réseau de tri de fusion pair-impair de Batcher (en),
- le tri bitonique,
- le tri de Shell et
- le réseau de tri par paires (en).
Ces réseaux sont souvent utilisés en pratique. D'autres, comme le réseau de tri pair-impair par transposition, sont plus simples à réaliser mais moins efficaces.
On peut aussi construire, au moins en théorie, des réseaux de taille arbitraire de profondeur logarithmique, en utilisant une méthode appelée réseau AKS, d'après ses inventeurs Ajtai, János Komlós, et Szemerédi[7]. Alors qu'il s'agit d'une découverte importante en théorie, le réseau AKS n'a que peu ou pas d'applications pratiques en raison de la constante de proportionnalité cachée dans la notation O, et qui s'élève à plusieurs milliers[1]:669. Pour toutes les valeurs « pratiques » de n, un réseau de profondeur O(log2 n) est plus efficace. La constante cachée est due en partie à la construction d'un graphe d'expansion employé dans la méthode. Une version simplifiée du réseau AKS a été décrite par Michael S. Paterson, qui note toutefois lui aussi que « la constante pour la borne de la profondeur rend toujours la construction impraticable »[8]. Une autre construction de réseaux de tri de taille O(n log n) a été découverte par Michael T. Goodrich (en)[9]. Même si sa constante est bien plus petite que celle du réseau AKS, sa profondeur, en O(n log n), la rend inefficace pour une implémentation en parallèle.
Réseaux de tri optimaux
Pour un nombre petit et fixé d'entrées, on peut construire des réseaux de tri optimaux, soit qu'ils sont de profondeur minimale (utile pour une exécution en parallèle), soit qu'ils comportent un nombre minimal de comparateurs (ils sont alors de taille minimale). Ces réseaux peuvent être employés dans une optique de construction récursive, comme briques qui améliorent les performances de réseaux plus grands. On peut ainsi arrêter plus tôt la construction récursive dans les réseaux de Batcher par exemple[10]. La table suivante donne les résultats d'optimalité connus :
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Profondeur[11] | 0 | 1 | 3 | 3 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 8 | 9 | 9 | 9 | 9 |
| Taille, majorant[12] | 0 | 1 | 3 | 5 | 9 | 12 | 16 | 19 | 25 | 29 | 35 | 39 | 45 | 51 | 56 | 60 |
| Taille, minorant (si différent)[12] | 33 | 37 | 41 | 45 | 49 | 53 |
Les seize premiers réseaux optimaux en profondeurs sont listés dans la section 5.3.4: « Networks for Sorting » du livre Art of Computer Programming de Knuth[3] et étaient déjà présents dans la première édition de 1973 ; l'optimalité des huit premières valeurs a été prouvée par Robert Floyd et Knuth dans les années 1960, alors que la preuve pour les six dernières valeurs date seulement de 2014[11]. Dans leur article, ils expriment le problème, après une réduction astucieuse, par des formules de logique propositionnelle, puis utilisent un logiciel de test de satisfiabilité. Les cas neuf et dix ont été résolus plus tôt, en 1991, par Parberry[10]. Une autre technique pour trouver des réseaux optimaux est décrite dans une page de Jason D. Hugues[13].
Des réseaux optimaux en taille sont connus pour un nombre d'entrées compris entre un et dix ; pour des valeurs plus élevées, des minorants de la taille S(n) peuvent être déduit inductivement d'un lemme dû à Van Voorhis : . Les dix réseaux optimaux sont connus depuis 1969, dont les huit premiers sont connus de Floyd et Knuth, mais l'optimalité des cas n = 9 et n = 10 n'a été prouvée qu'en 2014[12]. De nouveaux résultats (en 2017)[14] donnent une réponse sur l'optimalité en profondeur.
Notes et références
- Chapitre 27 : « Réseaux de tri », p. 681-700, dans Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction à l'algorithmique, Dunod, [détail de l’édition]

- (en) H. W. Lang, « Sorting Networks », Algorithmen - Sortieren - Networks, FH Flensburg, Allemagne, (consulté le ).
- Section 5.3.4: Networks for Sorting, pages 219–247, dans (en) Donald E. Knuth, The Art of Computer Programming, vol. 3 : Sorting and Searching, , 2e éd. [détail de l’édition].
- Brevet US 3029413 "Sorting system with n-line sorting switch", enregistré le 21 février 1957, publié le 10 avril 1962, déposé par Daniel G. O'Connor et Raymond J. Nelson
- K. E. Batcher, « Sorting networks and their applications » () (lire en ligne)
—Proc. AFIPS Spring Joint Computer Conference - J.D. Owens, M. Houston, D. Luebke, S. Green, J.E. Stone et J.C. Phillips, « GPU Computing », Proceedings of the IEEE, vol. 96, no 5, , p. 879 - 899 (DOI 10.1109/JPROC.2008.917757).
- Miklós Ajtai, János Komlós et Endre Szemerédi, « Sorting in c log n parallel steps », Combinatorica, vol. 3, no 1, , p. 1-19 (DOI 10.1007/BF02579338).
- Michael S. Paterson, « Improved sorting networks with O(log N) depth », Algorithmica, vol. 5, nos 1-4, , p. 75-92 (DOI 10.1007/BF01840378).
- (en) Michael T. Goodrich, « Zig-zag Sort: A Simple Deterministic Data-Oblivious Sorting Algorithm Running in O(n log n) Time », .
- Ian Parberry, « A Computer Assisted Optimal Depth Lower Bound for Nine-Input Sorting Networks », Mathematical Systems Theory, vol. 24, , p. 101–116 (lire en ligne)
- Daniel Bundala et Jakub Závodný, « Optimal Sorting Networks », Language and Automata Theory and Applications, , p. 236-247 (ISBN 978-3-319-04920-5, DOI 10.1007/978-3-319-04921-2_19, arXiv 1310.6271)
- La preuve est annoncée dans (en) Michael Codish, Luís Cruz-Filipe, Michael Frank et Peter Schneider-Kamp, « Twenty-Five Comparators is Optimal when Sorting Nine Inputs (and Twenty-Nine for Ten) », .. L'article en revue paraît en 2016 : Michael Codish, Luís Cruz-Filipe, Michael Frank et Peter Schneider-Kamp, « Sorting nine inputs requires twenty-five comparisons », Journal of Computer and System Sciences, Elsevier BV, vol. 82, no 3, , p. 551-563 (ISSN 0022-0000, DOI 10.13039/501100003977).
- (en) Jason D. Hugues, « Sorting networks and the END algorithm », Rabb School of Continuing Studies, Brandeis University (consulté le ).
- (en) Daniel Bundala, Michael Codish, Luís Cruz-Filipe, Peter Schneider-Kamp et Jakub Závodný, « Optimal-depth sorting networks », Journal of Computer and System Sciences, vol. 84, , p. 185–204 (DOI 10.1016/j.jcss.2016.09.004).
-
Ian Parberry « On the Computational Complexity of Optimal Sorting Network Verification » ()
— « (ibid.) », Proc. PARLE '91: Parallel Architectures and Languages Europe, Volume I: Parallel Architectures and Algorithms, Eindhoven, The Netherlands, , p. 252–269. - Ian Parberry, « On the Computational Complexity of Optimal Sorting Network Verification », dans PARLE '91: Parallel Architectures and Languages Europe, vol. I. Parallel Architectures and Algorithms, Springer, coll. « Lecture Notes in Computer Science » (no 505), , 252–269 p..
Lien externe
- Richard J. Lipton et Ken Regan, « Galactic Sorting Networks », sur Gödel’s Lost Letter and P=NP,






















