Réseau de diffraction
Un réseau de diffraction est un dispositif optique composé d'une série de fentes parallèles (réseau en transmission), ou de rayures réfléchissantes (réseau en réflexion). Ces traits sont espacés de manière régulière, et l'espacement est appelé le « pas » du réseau. Si la distance entre plusieurs traits est de l'ordre de grandeur de la longueur de cohérence spatiale de la lumière incidente, le réseau permet d'obtenir des figures de diffraction particulières influencées par la répétition. Il s'agit donc d'un effet de diffraction lié à la répétition d'une structure optique, distinct de l'effet issu de la diffraction par une structure de taille comparable à la longueur d'onde, comme une fente de Young.
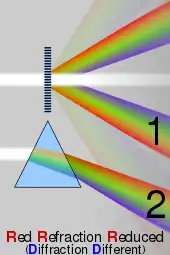

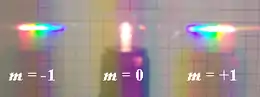
Lorsque la lumière blanche est incidente sur un réseau, celui-ci décompose la lumière sous différents angles, selon ses longueurs d'onde (ou couleurs) constitutives. Ce phénomène se produit de manière similaire à un prisme (voir image). Les réseaux sont donc utilisés dans de nombreuses applications, notamment les spectromètres et les monochromateurs. Si la lumière incidente est monochromatique (composée d'une seule longueur d'onde), le réseau réfléchit plusieurs taches ; la direction de réflexion des taches dépend de la distance entre les traits et de la longueur d'onde. La déviation est d'autant plus grande que la longueur d'onde est grande ou que le pas est petit.
Puisque les disques compacts ont une structure répétée de l'ordre de grandeur de la longueur d'onde de la lumière visible, on peut observer la diffraction de la lumière sur ceux-ci à l'œil nu. La lumière est diffractée par les pistes[note 1] constituées des bits et qui jouent le rôle des traits du réseau.
Histoire

En 1786, l'astronome américain, David Rittenhouse, réalisa un réseau de diffraction en transmission en tendant des cheveux entre deux pas de vis très fins (une cinquantaine de cheveux sur des filets de 116 puis 190 pas par pouce). Fraunhofer utilisa la même technique avec des fils métalliques en 1821[1]. Les réseaux furent ensuite gravés mécaniquement puis par photogravure.
Formules d'optique
Le principe des réseaux de diffraction repose sur une même formule pouvant être démontrée soit par l'optique physique, soit par la théorie électromagnétique de Maxwell. Il se base sur le principe de Huygens-Fresnel.
Le calcul sur un réseau est très similaire au calcul fait sur les fentes de Young (voir cet article) : la différence de marche entre deux traits (donc le déphasage des rayons diffusés par deux traits voisins) se calcule de la même manière. La différence est qu'au lieu d'avoir la somme de deux fonctions d'onde, on a la somme d'une série « infinie » (le nombre de traits étant très grand) :
en reprenant les notations des fentes de Young :
- x est l'abscisse du point sur l'écran de visualisation, sur un axe perpendiculaire aux traits du réseau ;
- E(x, t) est l'amplitude de l'onde à l'abscisse x et à l'instant t ;
- E0·sin(ωt ) est l'amplitude de l'onde incidente arrivant sur le trait 0, ω étant la pulsation ;
- est le déphasage entre deux traits voisins, avec
- V le pas du réseau ;
- D la distance entre le réseau et l'écran de visualisation de la figure de diffraction (écran parallèle au plan du réseau).
Si l'on est en condition de diffraction entre deux traits (cas des fentes de Young), on l'est également entre tous les traits : le déphasage est partout un multiple de 2π. On va donc avoir des maxima d'intensité en
ou bien, si l'écran est « à l'infini » (c'est-à-dire à plusieurs mètres ou bien dans le plan focal image d'une lentille convergente), on considère l'angle de déviation α donnant un maximum d'intensité :
Largeur des raies et taille du réseau
La différence entre un réseau et des fentes de Young est que, pour un réseau infini, l'intensité va s'annuler dès que l'on s'écarte des conditions de diffraction. Au lieu d'avoir un pic dont la forme est en cos2, on a un pic très fin : si l'on se place en xk + δx, alors
un trait i sera en opposition de phase avec le trait 0 s'il existe un entier j vérifiant
soit :
Dans le cas des fentes de Young, il n'y a annulation que lorsque λD/(2Vδx ) est entier ; ici, il suffit de prendre j suffisamment grand pour que la fraction devienne entière. En théorie (nombre infini de traits éclairés), l'intensité est donc nulle hors condition de diffraction (l'ensemble des réels est l'adhérence de l'ensemble des rationnels).
Dans la pratique, le réseau a un nombre fini de traits, et seule une portion du réseau est éclairée. Si l'on appelle N le nombre de traits éclairés, alors l'intensité s'annule pour la première fois lorsque
si N est impair, ou en
s'il est pair. La largeur du pic est donc divisée par N (ou N - 1) par rapport aux fentes de Young.
Le cas de la diffraction à l'infini peut se traiter dans l'espace réciproque.
Formule des réseaux
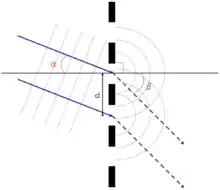
Lorsque la lumière est incidente sur un réseau de transmission, elle n'est réfléchie ou transmise qu'en certains points, les traits du réseau. Chaque trait diffuse la lumière dans toutes les directions, et ces ondes interfèrent (voir image). Comme les traits sont disposés de manière régulière, on a une alternance interférence constructive/interférence destructive selon l'angle de diffusion. On peut ainsi calculer, pour une longueur d'onde λ donnée, les angles θm pour lesquels on aura une interférence constructive[2] - [3].
- Réseau en réflexion
- Soit n1 l'indice du milieu de propagation de l'onde incidente (de longueur d'onde λ). Soit θi l'angle d'incidence et θm l'angle de réflexion pour lequel on a une interférence constructive. Soit d le pas du réseau et m un nombre entier. Comme on peut le déduire en regardant le schéma du réseau réflectif, il y a des interférences constructives si
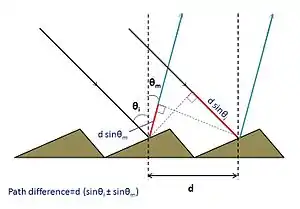
- Réseau en transmission
- Soit n1 l'indice du milieu de propagation de l'onde incidente (de longueur d'onde λ), et n2 l'indice du milieu transparent dans la fente du réseau (on peut avoir n1 = n2 si le réseau est une simple série de fentes vides). Soit θi l'angle d'incidence et θm l'angle de réfraction pour lequel on a une interférence constructrive. Soit d le pas du réseau et m un nombre entier. On a des interférences constructives si
Dans ces deux formules, les angles sont décrits par une valeur algébrique.
Le nombre m se nomme le « mode », ou encore « ordre de diffraction ». Dans chaque cas étudié, le nombre de modes se déduit des équations précédentes en notant que
- -1 ≤ sin θm ≤ 1
chaque longueur d'onde est donc diffractée dans plusieurs directions. En fait il existe plus de modes mais ceux-ci restent en surface du réseau.
Vocabulaire
- Dispersion angulaire
- On appelle dispersion angulaire la dérivée
- .
- Efficacité
- Soit Am l'amplitude de l'onde réfléchie à l'ordre m.
- L'efficacité ressemble en tous points au coefficient de réflexion d'une onde. On la définit, à l'ordre m, par :
- Intervalle spectral libre (ISL)
- Il est défini par le rapport
- .
- Il correspond à l'intervalle maximal de longueur d'onde pour qu'il n'y ait pas recouvrement d'ordre.
- Résolution
- La résolution est limitée car le réseau a une dimension finie (convolution par fonction porte d'un signal échantillonné, donc problème de recouvrement spectral). Elle est donnée par
- .
Applications
Les applications sont diverses en spectroscopie car l'angle de sortie dépend de la longueur d'onde étudiée. Ainsi, les réseaux sont utilisés dans les spectroscopes de type Littrow ou dans le montage de Czerny-Turner (voir l'article Analyse dispersive en longueur d'onde).
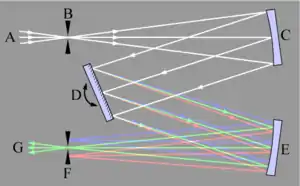
Les réseaux peuvent être utilisés comme monochromateurs : en choisissant une direction, on peut sélectionner une seule longueur d'onde. Il est donc possible de les utiliser dans les lasers accordables. On peut aussi graver un réseau dans une fibre optique (FBG, fiber Bragg grating )[4], et donc avoir une fibre qui sélectionne les longueurs d'onde transmise en fonction de son élongation ; cela permet de réaliser des capteurs de déformation ou de température (par le phénomène de dilatation).
De plus, lorsqu'un réseau se déplace d'une longueur , il introduit un déphasage de , donc grâce aux interférences entre les modes 1 et -1 on peut remonter au déplacement du réseau. On peut donc ainsi réaliser un capteur de déplacement de haute résolution.
Les réseaux sont également très utiles dans l'enseignement car ils permettent de comprendre les propriétés de la lumière ; ils sont souvent utilisés en travaux pratiques.
Il existe également des réseaux bidimensionnels, composé de lignes non parallèles ou de points. À la base, l'holographie consiste à créer un réseau bidimensionnel en impressionnant une pellicule photographique. La restitution de l'image est en fait la figure de diffraction sur ce réseau. Un autre exemple est la diffraction de la lumière sur un disque compact, les bits étant autant de points.
Il existe enfin des réseaux tridimensionnels : les cristaux. La structure cristalline est un objet périodique dont chaque atome est un site de diffusion. C'est la base de la diffraction de rayons X, de la figure de diffraction en microscopie électronique en transmission, des pseudo-lignes de Kikuchi (en) utilisée en EBSD (microscopie électronique à balayage), et de la diffraction de neutrons. Voir les articles Loi de Bragg et Théorie de la diffraction sur un cristal.
Nous avons vu ci-dessus que moins un réseau à une dimension a de traits, plus les pics de diffraction sont large. De même, moins un cristallite a d'atomes (plus il est petit), plus les pics sont larges. Cela permet d'estimer la taille de cristallite par diffraction de rayons X, voir l'article Formule de Scherrer.
Notes
- Les informations sont constituées d'éléments de longueur variables disposés sur une très longue spirale à pas régulier. C'est l'accumulation de ces pistes voisines qui crée l'effet de réseau. L'effet diffractant est perpendiculaire aux pistes, c'est-à-dire radial sur un disque.
- Les conventions de signe ne sont pas uniformes dans la littérature.
Références
- (en) Thomas S. Cope, The Rittenhouse diffraction gratting dans The scientific writings of David Rittenhouse (p.101) sur Google Livres, 1980, (ISBN 978-0-4051-2568-3)
- Christopher Palmer, Diffraction Grating Handbook, Richardson Gratings, , 7e éd. (lire en ligne), p. 27
- (en) B.E.A. Saleh, M.C. Teich, Fundamentals of Photonics, Hoboken, New Jersey, John Wiley & Sons, , 2e éd., p. 56
- Thierry Lucas, « Matériaux. Une boîte noire dans l'hélice », L'Usine nouvelle, Groupe industrie service info, no 3301, , p. 56 (ISSN 0042-126X)
















