Théorie de la diffraction

La théorie de la diffraction, dans sa forme élémentaire, repose sur le principe de Huygens-Fresnel. Selon ce principe, chaque point atteint par une onde se comporte comme une source secondaire. La figure de diffraction observée résulte de l'interférence des ondes émises par l'ensemble des sources secondaires. Bien que cette théorie ne fasse pas intervenir la nature de l'onde (sonore, lumineuse...), le vocabulaire et les illustrations de cet article seront empruntés au domaine de l'optique.

Le principe de Huygens-Fresnel est une approximation de la solution rigoureuse au problème de diffraction donnée par la résolution de l'équation d'onde. Il est valable dans le cadre de l'approximation paraxiale : c’est-à-dire quand la distance entre l'objet et la figure de diffraction est grande devant à la fois la taille de l'objet et la taille de la figure de diffraction.

Principe de Huygens-Fresnel

Énoncé

Soit une onde monochromatique incidente sur une ouverture. D'après le principe de Huygens-Fresnel, tout élément de surface de l'ouverture peut être considéré comme une source secondaire, se propageant de proche en proche (Huygens) et l'amplitude de l'onde émise par cette source secondaire est proportionnelle à la somme de chacun des éléments de surface de l'onde incidente (Fresnel). Les ondes émises par ces différentes sources interfèrent entre elles pour donner l'onde diffractée.

On trouve parfois une expression corrigée qui tient compte du fait qu'en toute rigueur la source ponctuelle n'est pas isotrope. Comme elle émet dans une direction privilégiée, on ajoute parfois un « facteur d'obliquité ». L'origine de ce facteur d'obliquité est à chercher dans la démonstration du principe de Huygens-Fresnel à partir de l'équation d'onde.

Expression mathématique

On considère une ouverture $\Sigma$ contenue dans le plan $z=0$ . Soit $E(P)=E(X,Y)$ l'amplitude de l'onde incidente en un point P quelconque de l'ouverture, de coordonnées $(X,Y)$ . L'amplitude de l'onde émise par la source secondaire de surface $\mathrm {d} \Sigma$ autour de $P$ est de la forme $K\cdot E(P)\cdot \mathrm {d} \Sigma$ où $K$ est une constante qu'il n'est pas utile de chercher à déterminer ici.

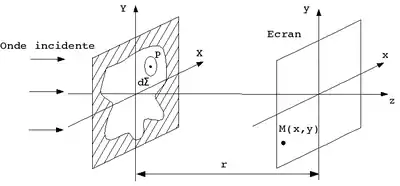
Lorsqu'elle arrive au point d'observation M, de coordonnées $(x,y)$ dans le plan $z=r$ , cette onde a pour amplitude, en notation complexe :

\mathrm {d} E(M)={\frac {1}{PM}}\cdot K\cdot E(P)\cdot \mathrm {d} \Sigma \cdot e^{i\varphi _{PM}}={\frac {1}{PM}}\cdot K\cdot E(P)\cdot \mathrm {d} \Sigma \cdot e^{i{\frac {2\pi PM}{\lambda }}}.

Le facteur 1/PM rend compte de l'atténuation de l'onde sphérique émise en P et $\varphi _{PM}$ représente le déphasage de l'onde entre P et M.

L'amplitude totale en M s'obtient en sommant les contributions de tous les points de l'ouverture, soit :

E(M)=K\iint _{\Sigma }{\frac {E(P)}{PM}}\cdot e^{i{\frac {2\pi PM}{\lambda }}}\cdot \mathrm {d} \Sigma .

Facteur de transmission

Les objets diffractants ne sont pas forcément des ouvertures laissant passer 100 % de l'onde au niveau de l'ouverture et rien à côté. Il peut s'agir d'objets atténuant l'onde de façon différente suivant le point considéré (diapositive par exemple, pour la lumière) et/ou d'objets introduisant un déphasage dépendant là aussi du point considéré.

Pour prendre en compte ces différentes possibilités, on introduit le facteur de transmission, ou transmission, t(P)=t(X, Y), d'un objet qui est le rapport entre l'amplitude de l'onde juste après l'objet avec celle de l'onde juste avant l'objet.

En notant E₀(P) l'amplitude de l'onde juste avant l'objet diffractant, l'amplitude de l'onde diffractée s'écrit alors :

E(M)=K\iint {\frac {E_{0}(P)}{PM}}t(P)e^{i{\frac {2\pi PM}{\lambda }}}d\Sigma

La transmission étant définie pour tout point P appartenant au plan de l'objet diffractant, les intégrales sont calculées de -∞ à +∞

Ce formalisme sera utilisé pour la diffraction de Fraunhofer.

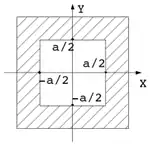
Exemples:

Ouverture carrée de côté a laissant passer 90 % de l'onde.

t(X,Y)=0,9\;\mathrm {si} \;|X|<a/2\;\mathrm {et} \;|Y|<a/2

t(X,Y)=0\;\mathrm {sinon}

Prisme carré de côté a, d'indice n et d'angle au sommet α (petit).

Un rayon lumineux incident à une distance y du sommet du prisme subit un déphasage φ=2πα y(n-1)/λ où λ est la longueur d'onde.

En supposant le prisme parfaitement transparent, la transmission s'écrit:

t(X,Y)=\exp(j\phi )\;\mathrm {si} \;|X|<a/2\;\mathrm {et} \;0<Y<a

t(X,Y)=0\;\mathrm {sinon}

Diffraction de Fresnel

La validité de cette théorie a été établie de façon spectaculaire par Arago avec l'expérience de la tache de Fresnel (1818).

Dans les conditions usuelles d'observation, les tailles de l'ouverture et du phénomène de diffraction observé sont petites devant la distance r d'observation. On a :

PM={\sqrt {r^{2}+(x-X)^{2}+(y-Y)^{2}}}

On peut donc utiliser un développement limité pour écrire:

PM\simeq r\left[1+{\frac {1}{2}}\left({\frac {x-X}{r}}\right)^{2}+{\frac {1}{2}}\left({\frac {y-Y}{r}}\right)^{2}\right]

En remplaçant PM par cette expression dans l'exponentielle complexe et 1/PM par 1/r (cette approximation est ici suffisante car 1/PM n'est pas une fonction périodique), on obtient alors :

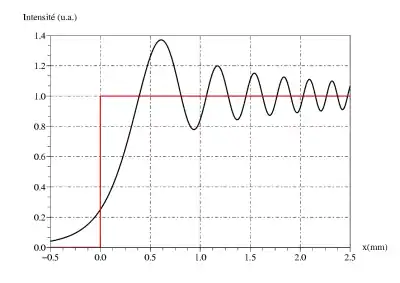
E(M)=K'\iint _{\Sigma }E(P)\exp \left[{\frac {j\pi }{\lambda r}}\left[(x-X)^{2}+(y-Y)^{2}\right]\right]dXdY

où $K'={\frac {K}{r}}e^{j{\frac {2\pi r}{\lambda }}}$ . Cette intégrale est appelée transformation de Fresnel et permet de déterminer la figure de diffraction observée à distance finie de l'ouverture diffractante. Ce genre de diffraction peut par exemple s'observer sur les bords de l'ombre géométrique d'un écran, comme illustré ci-dessous.

Courbe donnant l'intensité de la lumière diffractée par un bord d'écran observée à une distance r=1 mètre. La longueur d'onde est λ=0,5 micromètre. On observe que la largeur de la première oscillation est de l'ordre de √(λr), les autres oscillations sont plus rapides et moins marquées. L'intensité que l'on aurait en l'absence de diffraction est représentée en rouge.

Diffraction de Fraunhofer

La diffraction de Fraunhofer ou diffraction à l'infini est un cas particulier très important où le plan d'observation est situé loin de l'objet diffractant, celui-ci étant éclairé par une onde plane (source ponctuelle à l'infini) et défini par son facteur de transmission t(X, Y).

C'est ce phénomène qui fixe la limite ultime de résolution que l'on peut espérer d'un instrument d'optique.

Expression de l'onde diffractée

On supposera ici que la source est située sur l'axe du système et donc que E(P) est constant dans le plan diffractant. On peut alors écrire:

\exp \left[j{\frac {\pi }{\lambda r}}(x-X)^{2}\right]\simeq \exp \left[j{\frac {\pi }{\lambda r}}x^{2}\right]\exp \left[-j{\frac {2\pi }{\lambda r}}xX\right]

si ${\frac {X^{2}}{\lambda r}}\ll 1$ quel que soit X correspondant à un point de l'ouverture.

Donc, si d est une dimension caractéristique de l'ouverture (ex: diamètre pour une ouverture circulaire), on se trouve dans les conditions de la diffraction de Fraunhofer si

{\frac {d^{2}}{\lambda r}}\ll 1

d²/λr est parfois appelé nombre de Fresnel.

Le même raisonnement étant bien entendu valable aussi pour le terme (y-Y)², l'amplitude de l'onde diffractée dans les conditions de Fraunhofer s'écrit donc :

E(M)=K''\iint t(X,Y)\exp \left[-{\frac {2j\pi }{\lambda r}}(xX+yY)\right]dXdY

où le terme de phase constant lors de l'intégration, $\exp \left[j{\frac {\pi }{\lambda r}}(x^{2}+y^{2})\right]$ , et l'amplitude constante E₀(P) sont contenues dans la nouvelle constante K".

On remarque que l'amplitude diffractée est proportionnelle à la transformée de Fourier de la transmission t(X, Y). Plus précisément, si on note t la transformée de Fourier de t, E(M) est proportionnel à t(x*k/r, y*k/r) avec k le nombre d'onde égal à $2\pi /\lambda$ .

Physiquement, on constate que l'amplitude de l'onde diffractée ne dépend que de la direction d'observation (définie par les angles x/r et y/r), ce qui justifie le nom de diffraction à l'infini.

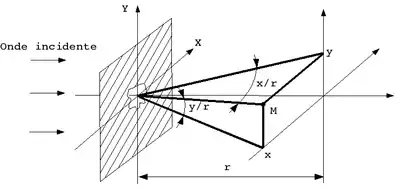
En pratique, observer à l'infini signifie être assez loin de l'objet diffractant pour que le nombre de Fresnel soit très inférieur à 1 ou, dans le cas de l'optique, se placer au foyer image d'une lentille. Dans ce dernier cas, la distance r doit être remplacée par la distance focale de la lentille, f, dans les formules précédentes.

Exemples de figures de diffraction

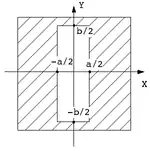
Diffraction par une ouverture rectangulaire

Une ouverture rectangulaire de côtés a et b correspond à une transmission t(X, Y) définie par :

t(X,Y) = 1 si |X|<a/2 et |Y|<b/2

t(X,Y) = 0 sinon

Le calcul de l'intensité diffractée par une telle ouverture, c’est-à-dire du carré du module de l'amplitude E(M), donne :

I(x,y)=|E(x,y)|^{2}=I_{0}\ \mathrm {sinc} ^{2}\left({\frac {\pi xa}{\lambda r}}\right)\mathrm {sinc} ^{2}\left({\frac {\pi yb}{\lambda r}}\right)

Dans cette expression, I₀ correspond à l'intensité maximale sur l'écran (au centre) et « sinc » est la fonction sinus cardinal définie par sinc(x)=sin(x)/x.

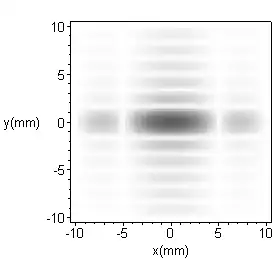
La figure ci-contre est une simulation de la figure de diffraction de Fraunhofer obtenue avec une ouverture rectangulaire de côtés a=0,1 mm et b=0,3 mm. On a pris λ=0,5 μm et on s'est placé au foyer image d'une lentille de distance focale f=1 m.

L'intensité des maxima secondaires a été artificiellement rehaussée afin de les rendre visibles.

En l'absence de diffraction, la figure obtenue aurait simplement été un point brillant au centre de l'écran correspondant à la focalisation par la lentille des rayons incidents parallèles à l'axe.

On remarque que le côté le plus petit correspond au plus grand étalement de la lumière. En effet, les dimensions de la tache centrale sont :

Δx=2λf/a=10 mm

Δy=2λf/b=3,3 mm

Diffraction par un rideau

C'est une application de l'exemple précédent. Lorsqu'une source de lumière quasiment ponctuelle est observée à travers un rideau ou un voilage, on peut voir des figures de diffraction telles celles-ci :

Voilages de cuisine classiques
Zoom vers une lumière extérieure allumée de jour
Zoom vers la même lumière extérieure mais de nuit
Idem, avec une luminosité permettant de mieux distinguer les lobes secondaires

Elles résultent de la diffraction de la lumière par le rideau, dont le tissu constitue tout un ensemble d'ouvertures carrées. La mesure de l'angle entre la tache centrale et sa voisine permet d'obtenir le pas du rideau.

Les irisations des taches proviennent du fait que chaque longueur d'onde construit sa propre figure de diffraction, légèrement différente de celle d'une longueur d'onde voisine. Les endroits où les figures coïncident sont blancs (en particulier la tache centrale), les autres sont colorés. On constate que la répartition des couleurs est logique car les maxima du sinus cardinal sont obtenus régulièrement (tous les $\Pi /2$ et x, distance d'un point au centre de la tâche, est proportionnel à $\lambda$

Diffraction par une ouverture circulaire

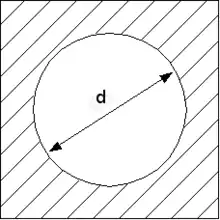
Ouverture circulaire de diamètre d.

Il est ici plus commode d'utiliser les coordonnées polaires $(R,\theta )$ plutôt que les coordonnées cartésiennes $(X,Y)$ . Une ouverture circulaire de diamètre d correspond alors à une transmission $t(R,\theta )$ définie par :

t(R,\Phi )=1

|R|<d/2

t(R,\Phi )=0

sinon.

Le calcul de l'intensité diffractée par une telle ouverture donne :

I(\rho )=|E(\rho )|^{2}=4I_{0}\left({\frac {J_{1}(\eta )}{\eta }}\right)^{2}

où $\eta ={\frac {\pi \rho d}{\lambda r}}$ et $\rho ={\sqrt {x^{2}+y^{2}}}$ .

La répartition d'intensité présente la même symétrie de révolution que la pupille. La figure obtenue est appelée tache d′Airy. Dans cette expression, $I_{0}$ correspond à l'intensité maximale sur l'écran (au centre) et $J_{1}(\eta )$ désigne la fonction de Bessel d'ordre 1.

Démonstration

On reprend la relation trouvée après avoir effectué l'approximation de Fraunhofer :

E(M)=K''\iint t(X,Y)\exp \left[-{\frac {2j\pi }{\lambda r}}(xX+yY)\right]\mathrm {d} X\mathrm {d} Y

On effectue un premier changement de variables afin d'utiliser les coordonnées cylindriques

{\begin{cases}X=R\,\cos \Phi \\Y=R\,\sin \Phi \end{cases}}

{\begin{cases}x=\rho \,\cos \theta \\y=\rho \,\sin \theta \end{cases}}

On obtient alors :

E(\rho ,\theta )=K''\int _{0}^{d/2}\int _{0}^{2\pi }\exp \left[-{\frac {2j\pi }{\lambda r}}R\,\rho \,\cos(\Phi -\theta )\right]\mathrm {d} \Phi \,R\,\mathrm {d} R

On simplifie l'expression en observant la complète symétrie axiale du problème. On se limite à chercher ce qu'il se passe pour $\theta =0$ :

E(\rho )=E(\rho ,0)=K''\int _{0}^{d/2}\int _{0}^{2\pi }\exp \left[-{\frac {2j\pi }{\lambda r}}R\,\rho \,\cos(\Phi )\right]\mathrm {d} \Phi \,R\,\mathrm {d} R

On introduit la fonction de Bessel :

J_{0}(u)={\frac {1}{2\pi }}\int _{0}^{2\pi }\mathrm {\exp } \left[\mathrm {j} .u.\sin \tau \right]\,\mathrm {d} \tau ={\frac {1}{2\pi }}\int _{0}^{2\pi }\mathrm {\exp } \left[\mathrm {j} .u.\cos \tau \right]\,\mathrm {d} \tau

L'expression prend alors la forme :

E(\rho )=K''\,2\pi \int _{0}^{d/2}J_{0}\left(-{\frac {2\pi }{\lambda r}}\,\rho \,R\right)\,R\,\mathrm {d} R

Pour exploiter la propriété des fonctions de Bessel selon laquelle $\int _{0}^{v}u\,J_{0}(u)\,\mathrm {d} u=v\,J_{1}(v)$ , on pose $u=-{\frac {2\pi }{\lambda r}}\,\rho \,R$ . On peut trouver $v=-{\frac {2\pi }{\lambda r}}\,\rho \,{\frac {d}{2}}=-\eta$ avec $\eta ={\frac {\pi \rho d}{\lambda r}}$ .

On peut en déduire que :

E(\rho )=K''\,2\pi \,\left({\frac {\lambda r}{2\pi \rho }}\right)^{2}\,(-\eta )\,J_{1}(-\eta )

ou encore :

E(\rho )=K''\,2\pi \,\left({\frac {d}{2\eta }}\right)^{2}\,\eta \,J_{1}(\eta )

Ce qui mène à :

E(\rho )=E(0)\,{\frac {2\,J_{1}(\eta )}{\eta }}

avec $E(0)=K''\,{\frac {\pi \,d^{2}}{4}}$ .

D'où, comme $I(\rho )=I(0)\,|E(\rho )/E(0)|^{2}$ ,

I(\rho )=4\,I(0)\,\left({\frac {J_{1}(\eta )}{\eta }}\right)^{2}

Simulation de la figure de diffraction obtenue.

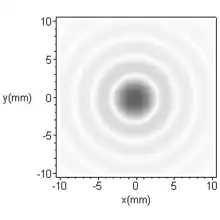
La figure ci-contre est une simulation de la figure de diffraction de Fraunhofer obtenue avec une ouverture circulaire de diamètre d = 0,2 mm. On a pris λ = 0,5 µm et on s'est placé au foyer image d'une lentille de distance focale r = f = 1 m. L'intensité des maxima secondaires a été artificiellement rehaussée afin de les rendre visibles.

Le rayon de la tache centrale vaut
$\Delta \rho =1,22\lambda \,f/d=3\ \mathrm {mm}$ .

Résolution d'un instrument d'optique

Le rôle de la plupart des instruments d'optique (microscope, objectif d'appareil photo, télescope…) est de former des images. Du point de vue de l'optique géométrique, un instrument « parfait », c'est-à-dire exempt d'aberrations, fait correspondre à un point objet un point image (voir aussi Stigmatisme).

En réalité, lors de leur cheminement à travers l'instrument, les faisceaux lumineux sont diaphragmés par les montures des lentilles et donc diffractés. L'image d'un point source par un instrument dépourvu d'aberrations n'est donc pas un point image mais une tache de diffraction. On peut montrer que la répartition d'intensité dans le plan de l'image est donnée par les formules de diffraction de Fraunhofer. Les montures des lentilles ou miroirs étant la plupart du temps circulaires, la figure de diffraction obtenue est une tache d'Airy décrite dans le paragraphe précédent.

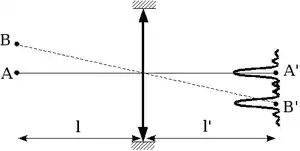
Ainsi, deux points objets rapprochés peuvent donner deux images trop proches pour être distinguées si la distance entre ces images est du même ordre de grandeur que la taille de la tache de diffraction. On appelle résolution l'écart minimal entre deux points objets pour qu'on puisse les distinguer avec l'instrument d'optique considéré.

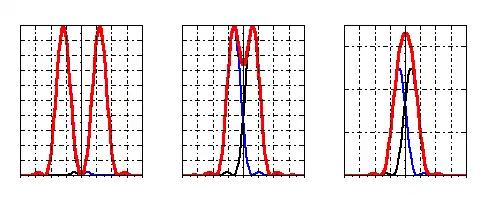
Quantitativement, pour déterminer la limite à partir de laquelle on ne peut plus distinguer les images A' et B' de deux objets A et B, on utilise le critère de Rayleigh : lorsque le sommet d'une des taches de diffraction correspond au premier minimum nul de l'autre, les pics sont trop proches pour qu'un observateur puisse les distinguer (voir illustration).

Les courbes bleues et noires montrent les intensités correspondant aux taches de diffraction de A' et B'. Les courbes rouges représentent l'intensité totale telle que perçue par un détecteur. Si A' et B' sont suffisamment éloignés (figure de gauche), les deux images sont nettement séparées. S'ils sont trop proches (figure de droite), on ne distingue qu'une seule tache. Le brouillage des deux images se produit approximativement lorsque le maximum d'une tache de diffraction correspond au premier minimum de l'autre. C'est le critère de Rayleigh.

Prenons le cas simple de la formation d'une image par une lentille mince de diamètre d. On note l la distance objet-lentille et l' la distance lentille-image. A' et B' sont séparés si

A'B'>1,22{\frac {\lambda }{d}}l'

Comme $AB=A'B'l/l'$ , la condition précédente devient:

AB>1,22{\frac {\lambda }{d}}l

En pratique, le rapport l/d est supérieur ou voisin de 1. La résolution est donc au mieux du même ordre de grandeur que la longueur d'onde de la lumière utilisée, entre 0,4 et 0,8 micromètre pour la lumière visible. Ce résultat est général.

Ceci explique par exemple pourquoi un microscope optique ne peut pas distinguer des détails inférieurs à quelques dixièmes de micromètre. Des résolutions bien meilleures peuvent par exemple être obtenues avec des microscopes électroniques.
D'autre part, la résolution s'améliore lorsque le diamètre augmente. C'est pourquoi les miroirs des télescopes font jusqu'à plusieurs mètres de diamètre.

Voir aussi

Liens externes

Théorie de la diffraction illustrée par des applets Java
(histoire des sciences) Premier mémoire de Fresnel sur la diffraction (1815), en ligne et commenté sur le site BibNum.

Bibliographie

José-Philippe Pérez, Optique : Fondements et applications [détail des éditions]
J.W. Goodman Introduction à l'optique de Fourier et à l'holographie, Édition Masson.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.