Réginald Outhier
Regnaud ou Renaud Outhier - pour l'état-civil - dit aussi l'abbé Outhier et qui signera certaines de ses œuvres Réginald Outhier, né à Lamarre-Jousserand le et mort à Bayeux le , est un ecclésiastique et un scientifique français du siècle des Lumières.

| Nom de naissance | Renaud Outhier, dit aussi Réginald Outhier ou l'abbé Outhier |
|---|---|
| Naissance |
Lamarre-Jousserand (Jura) |
| Décès |
(à 79 ans) Bayeux (Calvados) |
| Nationalité | Française |
| Domaines | Astronomie, géodésie |
|---|---|
| Institutions | Académie des sciences, arts et belles-lettres de Caen, Académie royale des sciences de Prusse, correspondant de l'Académie des sciences (France) |
| Renommé pour | ouvrage : Journal d'un voyage au Nord |
C'est un savant polymathe. Il s'intéresse à l'astronomie, à l'horlogerie et à la mécanique. Plus tard, il participe à des travaux géodésiques, réalise cartes et dessins et s'intéresse aux mathématiques. Il doit sa renommée à son ouvrage Journal d'un voyage au Nord qui relate, jour après jour, son implication et ce qu'il a vu dans l'expédition en Laponie de Maupertuis à laquelle il prend part.
Biographie

Réginald Outhier est né le à La Marre (-Jousserand), village du bailliage de Poligny anciennement en Franche-Comté. L’acte de naissance de Réginald Outhier n'a pas été retrouvé[N 1], l'identité de ses parents ainsi que la profession de son père ne sont donc pas certaines. D'après une enquête aux archives du Jura, Mario Morisi, écrivain jurassien, propose que Pierre Joseph, son géniteur, ait été « procureur d'office de Mirebel ». La famille Outhier était domiciliée au centre de La Marre, le quartier le plus important dit encore aujourd'hui « le quartier des Outhier », face à une croix très ancienne dédiée à « Sainte-Anne et Marie enfant » et à la chapelle Saint-Sauveur où priaient ses concitoyens[1] - [2] - [3].
Formation et début de carrière ecclésiastique
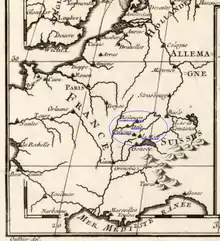
Les localités franc-comtoises les plus importantes dans la vie de Réginald Outhier ont été La Marre, Poligny, Dole et Besançon ; on le sait puisqu’il les a tracées lui-même sur sa carte d’une partie de l’Europe contenu dans son « Journal ». Il fait ses premières classes sans doute dans ce qui allait devenir le Collège de Poligny, puis à Dole, probablement chez les jésuites du Collège de l’Arc. Admis au séminaire de Besançon en 1714 à l'âge de vingt ans il y sera ordonné prêtre probablement avant la fin de 1717.
Après une période de trois années où on le voit apparaître en tant qu'« ecclésiastique » sur les registres de La Marre, où il aide le curé en charge, il est nommé vicaire à Montain, une paroisse éloignée d’une vingtaine de kilomètres de La Marre, comprenant, outre Montain, les villages de Lavigny, du Pin et du Louverot. Dans les anciens registres paroissiaux déposés aux archives départementales, c’est le qu’un acte porte pour la première fois la signature du vicaire Outhier. Le , il rédige et signe seul un de ces actes, et le 20 du même mois, l’acte de décès de son curé, le père Claude Chevillard (en office entre 1700 et 1730). C’est à cette date qu’il devient administrateur de fait de la paroisse. Le dernier acte signé de sa main est en date du ; le suivant, daté du , l’est par le nouveau curé Jacquemet seul, et à partir d’ apparaît le nom d’un nouveau vicaire[4] - [5].
J. Richard, dans son mémoire de 1926, écrira[6] : « Sa signature est très lisible, d’une écriture nette et régulière, sans autres ornements qu’un trait séparé, vigoureusement tracé, la prolongeant ou la soulignant ; si l’on en croit la graphologie elle dénoterait un esprit réfléchi, méthodique, très pondéré, bien que non dépourvu d’imagination, et aussi un caractère prudent et loyal. »
Une lettre d’Outhier signée à La Marre le est également connue (collection privée)[7].
Premières années scientifiques, 1726-1736
C’est en assumant sa charge de prêtre de campagne qu’Outhier entame ses importants travaux en astronomie et en horlogerie, discipline qui, depuis la fin du XVIe siècle, est une des fiertés de cette portion de la Franche-Comté.
Remarqué dans ses écrits par Jacques Cassini, membre de l’Académie royale des Sciences[8], il en deviendra un de ses correspondants scientifiques quelques années plus tard[9].
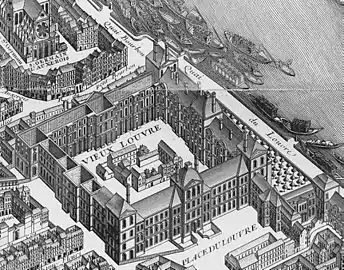
En 1726, il imagine un « globe mouvant » où les mouvements du Soleil et de la Lune se trouvaient figurés, permettant de visualiser ainsi les moments où pouvaient avoir lieu des éclipses. Le globe, exécuté par son ami horloger Jean-Baptiste Cattin, est présenté par son concepteur à l’Académie royale des Sciences en 1727 et 1731 (version perfectionnée)[10]. L’objet est alors reçu avec l’éloge suivante : « Quoiqu’il y ait déjà plusieurs ouvrages dans ce goût-là, on a trouvé que celui-ci était très ingénieusement imaginé, que quelques dispositions nouvelles, celle, par exemple qui regarde les phases de la lune et ses latitudes, le rendaient simple, et donnaient une idée avantageuse de l’intelligence et de l’habilité de l’inventeur. » ; Monnier[11] ajoute l’anecdote suivante : « L’abbé Outhier ayant porté ce globe à Paris, fut admis en 1732 à le présenter au Prince qui lui témoigna le désir de l’acquérir, et qui le pressa de lui dire quel prix il y mettait. Notre abbé qui ne savait pas que l’on ne vend rien au Roi, au lieu de lui faire hommage de son travail, eut la maladresse d’en fixer la valeur à quelques louis. La somme lui fut comptée ; et, par cette vente irréfléchie, le mérite de l’inventeur disparut sous le salaire de l’artisan. »
Le [N 2], Régnaud ou Renaud Outhier est invité à l’Académie des Sciences. Ce jour-là, il devient correspondant scientifique[12] de Jacques Cassini et on essaye de le retenir en le chargeant de réaliser calculs et plans de triangulation géodésique pour la future Grande Carte de France, mais il se soustraira assez vite à cette tâche fastidieuse.
À partir de 1732, sur les conseils de Cassini, il devient secrétaire [scientifique] près du jeune évêque de Bayeux, Mgr Paul d’Albert de Luynes nommé à ce poste en 1729 à l'âge de 26 ans et astronome et physicien éminent. Leur entente est si bonne qu'il résidera à l'évéché.
- Personnalités influentes
 Jacques Cassini pensionnaire de l'Académie.
Jacques Cassini pensionnaire de l'Académie. Paul d'Albert de Luynes, évêque de Bayeux.
Paul d'Albert de Luynes, évêque de Bayeux.
En 1733, il contribue, en tant que géomètre, au calcul de la perpendiculaire[N 3] - [13] à la méridienne de Paris pour la partie comprise entre Caen et Saint-Malo. C'est là qu'il approfondira ses connaissances pratiques en géodésie et cartographie. Cette expérience sera une sérieuse référence dans le choix de sa personne pour participer au « Voyage au Nord », dans les années suivantes.
Au service de Paul d'Albert de Luynes, une de ses tâches essentielles sera la réalisation de la carte du diocèse parue en 1736[14].
Le Voyage au Nord, 1736-1737

En 1736–1737, sur la demande du comte de Maurepas, alors secrétaire d'état à la marine, et avec le consentement de son évêque, Outhier s'engage à participer à l’expédition de Maupertuis en Laponie, « quoique prévenu contre le climat des pays du Nord ».
Cette expédition géodésique, qui consiste à mesurer un degré de latitude au Nord, a pour finalité de savoir si la Terre est sphérique, aplatie aux pôles ou à l'équateur. Les principaux membres de cette mission sont quatre titulaires de l'Académie royale des sciences de Paris, à savoir : le géomètre et chef de l'expédition Maupertuis, le géomètre Clairaut, le mécanicien Camus, l'astronome Le Monnier ainsi qu'Outhier, correspondant de Cassini (accessoirement aumônier du groupe). Celsius, alors professeur d'astronomie à Uppsala, agrée par le roi et aujourd'hui célèbre savant suédois[N 4], fera partie de l'équipe et jouera le rôle de facilitateur dans le pays.
Il est à remarquer qu'Outhier est le seul membre de la mission ayant une connaissance approfondie de la géodésie de terrain[N 5].
« C’est dans cette circonstance que la personnalité d’Outhier s’affirme avec éclat. Observateur précis et rigoureux, il travaille aux côtés de Maupertuis dans des conditions parfois extrêmes et il fait preuve de qualités physiques remarquables. Supportant avec la même sérénité la chaleur de l’été et le froid polaire, il contribue très largement à la réussite de l’expédition.[15] »
Au retour en France, le Roi gratifie plusieurs membres de l’expédition, y compris Celsius, d’une pension ; Maupertuis s’indigne en entendant qu’Outhier est dépourvu de cette faveur. « Il alla trouver le cardinal Fleuri [alors Premier ministre de Louis XV] : lui témoigna sa surprise de ce qu'on n'avait point donné de pension à M. Outhier qui avait travaillé plus que les autres dans ce voyage ; excellent observateur, très industrieux pour les instruments et pour leur graduation : déclara qu'il aimait mieux renoncer à sa pension que de voir M. Outhier sans récompense. Le cardinal fit donner à M. Outhier une pension de 1 200 livres sur une abbaye dont l'abbé lui écrivit très honnêtement, avec promesse de lui faire remettre la somme tous les ans exactement, et sans frais[16]. »
Au retour du Voyage au Nord, 1738-1748
De retour du Voyage au Nord, Outhier reprend ses fonctions de secrétaire scientifique auprès de Paul d'Albert de Luynes. Personnellement ou avec son évêque, il mène à bien différents travaux scientifiques cités simplement ici et développés plus loin.
Il trace à Bayeux et à Caen différentes méridiennes ébauchées par l'équipe de Jacques Cassini lors de leur passage en 1733. À cette époque les méridiennes sont fort utiles pour connaitre l'heure « exacte », notamment en astronomie.
Dans le domaine astronomique donc, il effectue différentes observations avec son protecteur, dans l'évêché de Bayeux, ou à Sommervieu, la résidence d'été située à quelques kilomètres de Bayeux.
- Lieux des observations d'Outhier et de Luynes
 Cour de l'ancien palais épiscopal.
Cour de l'ancien palais épiscopal. L'ancienne résidence d'été des évêques.
L'ancienne résidence d'été des évêques.
Sur commande, fort de son expérience en cartographie, il réalise plusieurs cartes topographiques où sont soulignés les repérages géodésiques de l'Académie, dont les siens propres et, pour faciliter la mesure des distances sur le terrain, il met au point un odomètre assez original.
Dans le domaine de la géodésie pure, pour le compte de Cassini de Thury et pour la carte de France, il reprend du service et effectue la triangulation entre Saint-Malo et Nantes.
Accessoirement, il s'essaiera, en mathématique, à résoudre à sa façon la quadrature du cercle ; il produira aussi quelques almanachs pour le méridien de Bayeux.
Mais sa renommée viendra surtout de son ouvrage Journal d'un voyage au Nord qu'il publiera en 1744[17] en France et en 1746 à Amsterdam.
Outhier et les académies
Au début des années 1730, comme vu précédemment, Outhier devient correspondant de Jacques Cassini, membre de l'Académie royale des sciences de Paris. En tant que tel, il participe à divers travaux géodésiques et présente différentes études parues dans les Mémoires de l'Académie (voir infra).
Le , l’abbé Outhier est candidat, en même temps que Le Monnier, au poste d’adjoint géomètre de l’Académie. C’est par une lettre de Maurepas, le Secrétaire d’État à la Marine et à la Maison du Roi, datée du que l’Académie apprend que le roi a choisi Le Monnier, premier sur la liste. Après cet échec, Outhier ne se représente plus[18].
- Extraits des PV de l'Académie du 21 et
 Proposition de nomination de Lemonnier et Outhier.
Proposition de nomination de Lemonnier et Outhier. Choix du roi d'après une lettre de Maurepas transmise à l'Académie.
Choix du roi d'après une lettre de Maurepas transmise à l'Académie.
En 1756, à la mort de Jacques Cassini, son fils César François dit Cassini de Thury le reconduit dans cette fonction en raison des travaux effectués pour les levés de la carte de France[12] - [19]. Dans ses remerciements à ses collaborateurs sur le terrain, Cassini de Thury citera en premier Outhier, soulignant par là sa reconnaissance et le respect pour son engagement, son sérieux et l'exactitude de ses relevés[20].
En 1733, Outhier est élu membre de l’Académie royale des Belles-Lettres de Caen (fondée par Moisant de Brieux en 1652).
Un des objectifs de Paul d'Albert de Luynes, en arrivant dans son évêché, était de réveiller cette vieille assemblée qui somnolait depuis plusieurs décennies ; il l'installe alors dans son palais épiscopal de Caen et y présente Outhier - qui était attaché à sa personne. Le fait que ce dernier soit correspondant de l'Académie des sciences, ainsi que ses travaux du moment ont assurément joué en faveur de son élection. En 1754, âgé alors de soixante ans, il donne sa démission et est nommé académicien vétéran.
En 1746, invité par Maupertuis à le rejoindre à l'Académie de Berlin - ce qui montre l'estime que ce dernier lui portait -, Outhier, après de probables hésitations[N 6], en deviendra membre en 1747 au même titre que Diderot, Lalande, Voltaire et quelques autres Français, mais il ne se rendra jamais à Berlin[21].
Il a été associé de quelque manière aux travaux de l’ Académie des Sciences, Belles-Lettres et Arts de Besançon (fondée en 1752) mais rien n’indique une nomination formelle. C’est par la relation de l’abbé Outhier que le marquis de Montrichard, de l’Académie de Besançon, prend connaissance de l’orge de Laponie qui est très résistant au froid[22].
À noter qu’Outhier est jusqu’à la fin identifié comme « prêtre du diocèse de Besançon » et qu'il a maintenu des liens intellectuels avec cette ville puisqu’il offre un exemplaire de son Journal à la bibliothèque du Grand séminaire de Besançon avec le dédicace « Seminarii bisuntini dono autoris »[23].
 Le palais épiscopal de Caen.
Le palais épiscopal de Caen. L'entrée de l'Académie à Berlin.
L'entrée de l'Académie à Berlin. L'entrée du grand séminaire de Besançon.
L'entrée du grand séminaire de Besançon.
Une fin de vie paisible et studieuse, 1748-1774

En 1748, il devient chanoine ; il reçoit de son évêque « collation du canonicat et de la prébende du Locheur en sa cathédrale de Bayeux… L'abbé Outhier est porté présent à toutes les réunions, de février 1749 inclus à juillet 1764 inclus [24]».
En 1753, Paul d'Albert de Luynes est nommé à l’archevêché de Sens. Outhier ne le suivra pas et restera sur Bayeux : le successeur de l'évêque de Bayeux, Pierre-Jules-César de Rochechouart s'étonne, lors de son installation, de la résidence de l'abbé dans les locaux de l'évêché. Ce dernier est prié de quitter les lieux et se cherchera une habitation à proximité.
Le , l’abbé Outhier « infirme de corps à cause de son âge avancé et toutefois sain d’esprit et d’entendement[25] » avait donné procuration pour résigner « entre les mains de Notre Saint Père le Pape, Mgr le Chancelier ou tout autre » ses canonicat et prébende en faveur du Sieur René d’Etreham, sous la réserve d’une pension et rente viagère de 700 livres, à prendre sur le plus clair des revenus du bénéfice. Or, Rome n’accepta pas cet arrangement car il manquait au dossier un certificat de bonne vie et mœurs, saine doctrine, et d’idonéité et capacité à posséder les bénéfices ecclésiastiques. Un litige tortueux qui opposa Outhier et d’Etreham s’ensuivit ; c’est seulement le que le transfert eut définitivement lieu[26]».
L’abbé Outhier « se retira dans une petite maison qu’il avait acquise près du couvent de la Charité »[27]. Il y partagea son temps « entre l’étude et la prière » pendant dix ans et s’éteignit le à l’âge de 79 ans dans un ancien manoir[28] encore visible aujourd'hui, situé au 13 rue Montfiquet[29] et appelé le « Manoir Guérin de la Houssaye ». Comme membre de la paroisse Saint-Patrice, l'abbé est inhumé le lendemain[30] dans la chapelle de l’Immaculée Conception de la Sainte Vierge de l’ église de ladite paroisse. Aucun portrait d'Outhier ne nous est connu.
- Église Saint-Patrice, sépulture d'Outhier
 Une vue de l'église Saint-Patrice.
Une vue de l'église Saint-Patrice. Le chœur ; à droite vers la chapelle de la Vierge.
Le chœur ; à droite vers la chapelle de la Vierge.
Travaux publiés
Les domaines présentés suivent à peu près l'ordre chronologique des travaux de l'abbé ; son ouvrage Journal d’un voyage au Nord fait l'objet d'une section particulière.
Globe mouvant
Le globe mouvant inventé par l'abbé Outhier se conjugue suivant deux versions très proches dans leur conception.
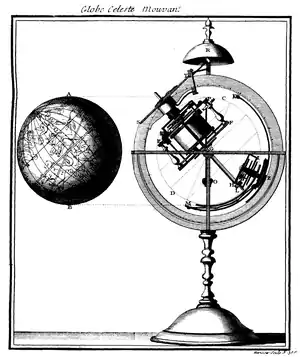
Cette première « invention » est un globe céleste « qui, quoiqu'il y ait déjà plusieurs ouvrages dans ce goût là, donne une idée avantageuse de l'intelligence et de l'habileté de l'inventeur[31]. »
Description[32] :
Monté sur un pied comme une sphère armillaire, avec son horizon et son méridien, il comprend essentiellement :
- le globe céleste mouvant, en cuivre [ou laiton], dont l'axe des pôles est incliné sur l'horizon de 49°, sensiblement la latitude de Paris. Il tourne autour de son axe en un jour sidéral, soit 23 h 56 min 04 s. « Sur ce globe sont gravées la plupart des étoiles fixes avec les constellations et tous les cercles de la sphère. » La Terre est supposée être au centre du globe ;
- au pôle nord, on trouve un cadran horaire muni d'une seule aiguille, celle des heures ;
- au zénith, un timbre sonne les heures en passant ;
- vers le pôle sud, du pôle méridional de l'écliptique partent deux bras portant respectivement le Soleil et la Lune ;
- le Soleil, noté en K sur la figure, est animé de son mouvement diurne (autour du globe) et de son mouvement annuel (par déplacement sur l'écliptique) ;
- la Lune, elle notée en M, est animée de son mouvement journalier et de son déplacement angulaire mensuel par rapport à l'écliptique. Un dispositif ingénieux permet de visualiser ses différents phases.
Parmi les fonctions de ce globe, on peut souligner la visualisation du lever, passage au méridien et coucher des deux astres. La fonction la plus intéressante est sans conteste d'indiquer une possibilité d'éclipse lorsque Soleil et Lune sont en conjonction (éclipse de Soleil) ou opposition (éclipse de Lune).
Mécanisme :
La figure montre la division interne initiale du mécanisme. Dans la partie supérieure, vers le pôle arctique, se trouvent les rouages horaires : un mouvement classique avec échappement et pendule et la complication pour donner la rotation au globe suivant le jour sidéral ; un rouage pour la sonnerie complète ce mécanisme.
Dans la partie basse, vers le pôle septentrional H et le pôle de l'écliptique Z, se trouvent les mécanismes assurant les mouvements diurnes des deux astres et le mouvement mensuel pour la Lune et annuel pour le Soleil.
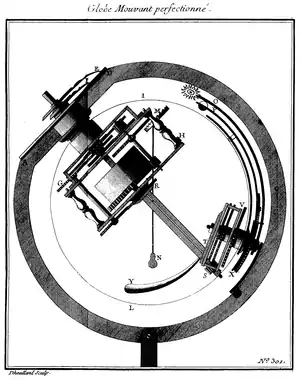
Dans cette version[33], l'abbé Outhier, sur le conseil de plusieurs personnes de l'Académie, va supprimer la sonnerie et adjoindre au cadran horaire une aiguille des minutes.
L'inventeur propose aussi un moyen pour agir sur la longueur du pendule sans entrer dans le mécanisme qui se trouve à l'intérieur du globe ; ce réglage permet d'ajuster l'avance ou le retard de temps affiché sur le cadran en fonction des variations de la température ambiante.
La présentation à l'Académie de la première version du globe a lieu le samedi devant l'Assemblée où on trouve, entre autres : Pajot d'Ons-en-Bray, membre honoraire ; Jacques Cassini, Maraldi, Chevallier, pensionnaires ; Maupertuis, Duffay, associés. Ces personnalités se retrouveront à plusieurs reprises dans la description des travaux de l'abbé.
Ce jour, « M. Outhier, curé en Franche-Comté a fait voir une machine qui représente les mouvements du Soleil et de la Lune, pour laquelle on a nommé Messieurs Cassini et Duffay[34]. »
Le , Cassini et Duffay, après avoir examiné le globe céleste d'Outhier, le présentent devant l'Assemblée ; Fontenelle, le secrétaire perpétuel en fera le compte-rendu[35].
Il subsiste quelques exemplaires du globe mouvant de l'abbé Outhier :
- le premier identique à la première version, avec une sphère en métal doré, a été mis en vente chez Jonathan Snellenburg en 2001-2008 (le site « Jonathan Snellenburg » est résilié.) ;
- deux autres globes identiques à la seconde version se trouvent au musée maritime national de Greenwich[36] ; d'autre part, Jonathan Snellenburg en mis un autre à la vente en 2001-2008 ;
- un dernier, du même type, fait partie des collections du Musée des Arts et métiers. Seul le mécanisme subsiste[37]. Il provient des cabinets de Pajot d'Ons-en-Bray pour qui Outhier réalisera une carte de son comté d' Ons-en-Bray.
 Le mécanisme de la seconde version, Musée des Arts et métiers.
Le mécanisme de la seconde version, Musée des Arts et métiers.
Mémoire sur la régulation des pendules à ressort
Le , « M. Outhier est entré [dans la salle de l'Académie] et a lu un mémoire sur la manière de perfectionner le mouvement des pendules à ressort[38]. ».
Ce mémoire, très technique, comprend six page de description accompagnées d'une illustration faite de quatre figures[39].
 Mécanisme.
Mécanisme.
Il ne semble pas que ce perfectionnement soit passé à la postérité ; il ne sera pas décrit ici.
Géodésie, triangulation
Formé à la triangulation théorique par Jacques Cassini dès 1731, secrétaire scientifique de Paul d'Albert de Luynes en 1732, l'abbé Outhier va s'investir dans des relevés géodésiques en Bretagne et en Normandie, que ce soit pour l'Académie et la future Carte de France ou pour son évêque qui lui réclame une carte topographique de son diocèse levée géométriquement.
De Caen à Saint-Malo
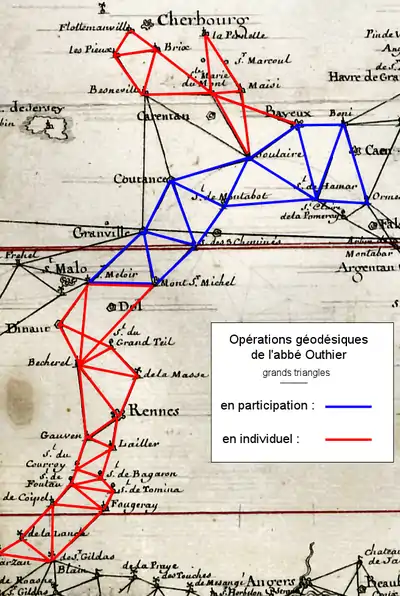
En 1733, « M. l'abbé Outhier travaille avec nous [l'équipe de Cassini] à la description de la perpendiculaire à la méridienne de Paris, depuis Caen jusqu'à Saint-Malo »[40].
Sur le terrain, il va côtoyer les principaux membres de l'équipe : Maraldi II, Jacques Cassini et ses fils, et d'autres géographes : Jean Delagrive et François Chevallier[41].
À leur contact, il approfondit ses connaissances pratiques. D'une part dans l'établissement des triangles (mesures sur le terrain à l'aide d'un quart de cercle mobile), dans la détermination d'une base près de Granville et le tracé d'une méridienne à Caen et à Bayeux - toutes ces notions étant nécessaires pour réaliser une bonne triangulation. D'autre part, au contact de Delagrive et de Chevallier, il s'initie à la cartographie. Ses compétences le rendent alors autonome et il pourra mener seul d'autres triangulations et réaliser aussi quelques cartes particulières, de diocèses notamment.
Sur la côte normande
En 1736, Outhier va publier « une carte topographique du diocèse de Bayeux levée géométriquement et assujettie aux observations de Messieurs de l'Académie[N 7] » ; sur cette carte sont soulignés tous les points objets de triangulation.
À l'origine, en 1733, l'équipe de Cassini s'arrête à Bayeux, chez l'évêque. Ils tracent au sol dans la bibliothèque de l'évêché une méridienne et « observent sur la tour de la cathédrale les angles entre divers objets aux environs pour déterminer leur situation par rapport à ceux qui étaient déjà connus[42] » ; c'est à partir de ces points que l'abbé va trianguler le diocèse et ébaucher le contour des côtes jusqu'à Cherbourg.
Comme instrument il emploie un quart-de-cercle un peu déréglé, mais qu'il saura compenser. Ses observations, d'après Cassini de Thury sont très exactes. Dans ses investigations, il repère une plage assez grande qui sera utilisée pour l'établissement de l'une des dix-huit bases géodésiques du canevas de la carte de France, la base dite de l'île « Saint-Marcou »[43] (plus 11 km).
Après 1739, « il achève ce qui reste des côtes de la Normandie du côté de Cherbourg »[N 8] - [44].
De Saint-Malo à Nantes
En 1737[45], Cassini de Thury confie à l'abbé Outhier, au retour du Voyage au Nord, la triangulation pour joindre Saint-Malo à Nantes en suivant la direction du méridien de Rennes.
Cette triangulation comporte 16 triangles dont le premier côté du premier triangle, au nord, joint Saint-Meloir au mont Saint-Michel et dont l'extrémité sud est à Marzan, au-dessus de Guérande, près de la base de Savenay qui servira de vérification[46]. Les triangles sont présentés dans le détail dans l'ouvrage de Cassini de Thury.
Ce travail, mené avec une précision extrême, sera vérifié par Cassini lui-même et revérifié par Méchain quelque quarante ans plus tard : les résultats « ont donné confirmation de l'exactitude des opérations de M. Outhier »[47].
Autres triangulations
L'abbé Outhier, dans les cartes qu'il publie, souligne toujours les points déterminés géométriquement. Ce sera le cas, outre la carte du diocèse de Bayeux déjà évoquée, des cartes du comté d'Ons-en-Bray et de l'archevêché de Sens (voir infra).
La triangulation effectuée en Laponie par l'équipe de Maupertuis sera reprise dans l'ouvrage de l'abbé ; elle sera présentée dans la section correspondante.
Cartographie
« Les méthodes géométriques mises au point par l'Académie des sciences et les travaux qu'elle exécute ont une influence sur la cartographie non officielle dès la fin du XVIIe siècle et principalement dans la première partie du XVIIIe siècle ».
Les cartes de diocèses en sont le plus bel exemple et les deux principales cartes de l'abbé Réginald Outhier (Bayeux et Sens) s'inscrivent dans cette catégorie. On peut y ajouter sa carte du comté d'Ons-en-Bray qui suit les mêmes exigences : ces cartes très ornées comme le veut l'époque se doivent d'être contrôlées par les membres de l'Académie et notamment par Cassini de Thury[48].
Carte du diocèse de Bayeux, 1736
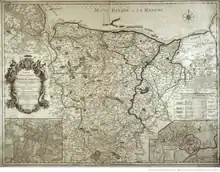
Cette carte topographique[50] est dédiée à Paul d'Albert de Luynes, évêque de Bayeux qui est le protecteur d'Outhier. Gravée au 1 : 130 000, « elle est levée géométriquement, selon ses ordres, par Monsieur Outhier, prêtre ; assujettie aux observations de Messieurs de l'Académie et aux opérations de Monsieur de Cassini… »
Elle comporte la carte proprement dite où sont soulignés les points déterminés de façon géométrique - plus de 100 points, en y incluant les signaux de M. Cassini - ; sur son pourtour on y voit son cartouche orné, la division du diocèse en paroisses, et un renvoi (légende) avec son échelle, plus de quarante signes distinctifs, et même les jours de marché.
Dans les coins inférieurs sont placés les plans de Bayeux et de Caen avec leurs remarques (légende), leur échelle et leur localisation suivant le méridien et le parallèle du lieu.
 Plan de Bayeux.
Plan de Bayeux. Plan de Caen.
Plan de Caen.
Carte du comté d'Ons-en-Bray, 1740
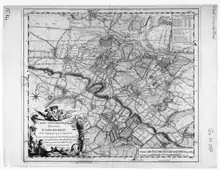
Pajot d'Ons-en-Bray et Outhier se connaissent depuis 1727, date à laquelle Outhier présente un globe mouvant à l'Académie ; au retour de Laponie, Louis-Léon Pajot commande à l'abbé une carte de son comté situé tout près de Thury-sous-Clermont où les Cassini ont demeure.
Cette carte[51] au 1 : 25 000, quoique plus simple que celle de Bayeux, est exécutée avec le même soin et avec les mêmes contraintes : elle est « levée géométriquement par M. l'abbé Outhier correspondant de l'Académie des sciences, assujettie aux observations de Messieurs de la dite académie et aux opérations de M. de Cassini ».
On y trouve, en plus d'un cartouche orné, un cadre où sont indiquées les distances des principaux endroits par rapport à la méridienne de Paris et à sa perpendiculaire ainsi que quelques latitudes et longitudes de lieux particuliers.
Carte du diocèse de Sens, 1741

Son commanditaire est Jean-Joseph Languet de Gergy archevêque de Sens et membre de l'Académie française ; nul doute que Joseph Languet et Paul d'Albert de Luynes se connaissent et se fréquentent, notamment à cause de leur présence à la Cour et à leurs positions respectives sur le jansénisme[N 9].
La carte topographique[52] au 1 : 180 000 est calquée dans ses grandes lignes sur celle de Bayeux.
Dans son cartouche orné, l'abbé se qualifie comme « prêtre du diocèse de Besançon, correspondant de l'Académie des sciences ».
Sur la carte proprement dite sont soulignés 131 points géodésiques dont 24 à 27 sont dus à M. Cassini.
Sur son pourtour on y voit son cartouche orné, la division du diocèse en archidiaconés et doyennés, un cadre où sont données les explications des renvois avec plus trente-huit signes distinctifs et, en bas l'échelle.
Dans le coin supérieur gauche est placé un plan de Sens et de ses faubourgs, avec son échelle et ses renvois ; dans le coin inférieur droit, suivant le même principe, on trouve un plan du château de Fontainebleau où sont repérés une vingtaine de lieux particuliers.
 Plan de Sens.
Plan de Sens. Plan du château de Fontainebleau
Plan du château de Fontainebleau
Carte de l'évêché de Meaux
Selon certaines publications biographiques du XIXe siècle, il aurait été publié une carte de l'évêché de Meaux, attribuée à Outhier, en 1717. Cette référence semble douteuse : à cette date, l'abbé n'a que 23 ans d'une part et, d'autre part, cette carte d'Outhier n'existe pas dans les archives nationales ni dans celles de l'évêché de Meaux qui ont été victimes d'incendie. D'après d'autres sources (Danville notamment), il faudrait plutôt attribuer cette carte à Chevallier qui l'aurait publiée dès 1698 ; une édition de 1717, dédiée à l'origine à Bossuet, existe bien à la BnF[53].
Mécanique
Fort de ses connaissances en horlogerie, l'abbé va perfectionner un instrument de mesure de distances dont il a fait usage dans la topographie de ses cartes : l'odomètre.
Odomètre
Sur le terrain, L'abbé Outhier emploie deux types d'instruments pour mesurer des distances nécessaires à sa cartographie :
- le premier est un quart de cercle mobile qui va lui permettre de mesurer des angles et par là de calculer de grandes distances par triangulation ;
- le second est un odomètre, instrument employé pour mesurer des distances secondaires liées au canevas des triangles définis géométriquement.
L'odomètre employé par l'abbé et fixé sur sa voiture, est à l'origine un instrument de M. Meynier, présenté à l'Académie en 1724[54]. À l'usage cet instrument s'est révélé présenter un défaut majeur : lors de reculs, parfois nécessaires dans les mesurages, l'aiguille de l'odomètre s'arrête et ne décompte pas ces phases de recul, faussant les résultats finaux attendus.
Ainsi, par exemple, soit à mesurer une distance de 120 unités : on mesure, depuis une origine, 100 u (affichage 100) puis on recule de 20 u (affichage 100) ; on est alors à 80 u de l'origine ; on repart jusqu'au but, la distance restant à parcourir est de 120 - 80 = 40. Est affiché finalement : 100 + 40 ; le résultat est faussé du recul non décompté.
L'abbé perfectionne cet instrument, supprime son défaut rédhibitoire et l'utilise dans ses levés cartographiques. Il le présente à l'Académie en 1742[55].
Son mécanisme est décrit dans le Recueil des machines approuvées par l'Académie, une illustration accompagne le propos[56].
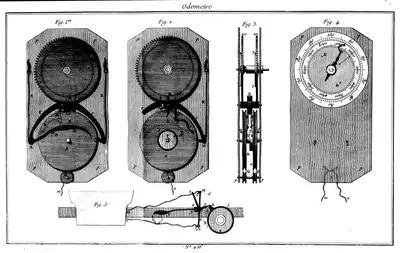
Dans ses conclusions, l'Académie recommande « d'en faire usage pour perfectionner la description topographique du royaume » ; dans celles du Recueil des machines, est évoqué un autre type d'odomètre dont M. d'Ons-en-Bray a discuté avec M. l'abbé Outhier. Plus tard, dans l' Encyclopédie méthodique de 1785, l'odomètre d'Outhier est cité : « dans l'odomètre de l'abbé l'aiguille recule quand le voyageur recule ; en sorte que l'odomètre décompte de lui-même tous les pas (sic) de trop que l'on a fait en arrière »[57].
Astronomie
L'abbé Outhier et son protecteur, Paul d'Albert de Luynes, ont observé le ciel conjointement au début des années 1740 puis, Luynes étant le plus souvent à Versailles, l'abbé observe seul jusqu'en 1762, date de sa dernière publication à l'Académie ; il a alors 68 ans. À cette époque, l'astronomie d'observation est surtout centrée sur les éclipses de Lune qui permettent la détermination des longitudes ; cette détermination implique la mesure du temps et nécessite l'usage de méridiennes qui soient les plus précises possible pour éviter les erreurs de localisation.
Méridiennes
1 - La méridienne de Caen
En 1733, dans sa marche vers Saint-Malo, Jacques Cassini va s'arrêter à Caen sur les terres de l’évêque qui y possède un « palais ». Ce dernier accueille toute l’équipe d’astronomes-géodésiens et, à l’ abbaye aux Dames où une des parentes de Luynes est abbesse, l’équipe de Cassini trace une méridienne horizontale – par besoin géodésique et aussi peut-être suivant les désirs de leur hôte. l'abbé Outhier affinera plus tard son tracé, en tant que secrétaire scientifique de l'évêque et, en tant que membre de l’Académie des sciences, arts et belles-lettres de Caen.
M. Outhier l’acheva.
De cette méridienne, il ne reste rien aujourd’hui, ni au sol, ni dans les archives.
2 - La méridienne de Bayeux
Toujours en 1733, au retour de St Malo, Cassini et son équipe passent par Bayeux, résidence principale de l’évêque qui les a probablement invités. Ils y restent quelques jours, effectuant des relevés géodésiques localisant la ville et déterminant la latitude astronomique du lieu. Pendant leur séjour, ils tracent une méridienne dans la bibliothèque de l’évêché, évènement relaté dans les Mémoires de l’Académie des Sciences par Jacques Cassini :
« Nous fîmes diverses observations de hauteur du Soleil, d’étoiles fixes, & principalement de l’Étoile polaire, dans le Palais épiscopal qui joint à la Cathédrale, & où M. l’Evêque de Bayeux a fait tracer dans sa bibliothèque une grande Méridienne, avec des lignes qui marquent les heures avant & après midi, de cinq en cinq minutes, par M. l’Abbé Outhier… » [59].
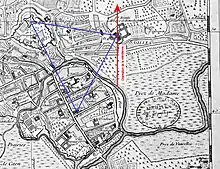
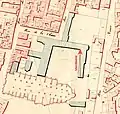 Localisation de la méridienne de Bayeux.
Localisation de la méridienne de Bayeux. Tracé théorique de la méridienne horizontale.
Tracé théorique de la méridienne horizontale.
Comme pour la méridienne de Caen, cette dernière, horizontale, a été mise en place pour besoins géodésiques. Elle a vraisemblablement servi par la suite à l’évêque et à Outhier pour leurs observations personnelles.
3 - La méridienne de Sommervieu
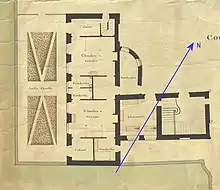
On rappelle que Sommervieu est la maison de campagne de l’évêque ; elle est située à 3 km au N-E de Bayeux.
Jacques Cassini rapporte, dans les Mémoires de l’Académie, des observations effectuées par l’évêque et Outhier d’une éclipse (occultation) de Jupiter par la Lune :
« Le , M. l’évêque avait réglé depuis longtemps sa pendule par le passage de plusieurs étoiles fixes dans la lunette d’un arc de cercle scellé très solidement dans le mur depuis trois ans, & vérifié souvent ; ainsi il en connaissait exactement la marche, & il a pris avant et après l’observation, le passage du Soleil par le méridien à une méridienne fort juste & fort solide qu’il avait vérifiée depuis quinze jours par des hauteurs correspondantes prises avec tout le soin possible[60]. »
La localisation de la méridienne et de l’arc de cercle à lunette utilisé pour régler la pendule n'est pas précisée : L’évêque entretient un laboratoire jouxtant sa chambre, ce lieu ne semble pas judicieux pour installer une méridienne, l’aile occidentale du bâtiment bouchant la vue du sud vers l’ouest. Le local serait plutôt à l’étage où l’horizon est plus dégagé[N 10] - [61].
Observations
Une dizaine d'observations sont inscrites dans les publications de l'Académie.
| Année | Observation | Lieu | Instrument |
|---|---|---|---|
| 1743 | Éclipse de Lune[62] | Bayeux | Lunette type ? |
| 1744 | Éclipse de Jupiter par la Lune[63] | Sommervieu | Lunette de 8 pieds (2,6 m) |
| 1748 | Éclipse de Soleil[64] | Bayeux | Lunette de 2 pieds (0,65 m) et de 13 pieds (4,2 m) |
| 1748 | Éclipse de Lune[65] | Bayeux | Lunette de 2 pieds (0,65 m) |
| 1749 | Éclipse de Lune[66] | Bayeux | d° |
| 1750 | Éclipse de Soleil[67] | Bayeux | d° |
| 1750 | Carte des Pléiades[68] | Bayeux ? | Lunette de 15 pieds (4,9 m) |
| 1761 | Éclipse de Lune[69] | Bayeux | Lunette de 34 pouces (0,92 m) |
| 1761 | Passage de Vénus sur le Soleil[70] | Bayeux | d° |
| 1762 | Éclipse de Lune[71] | Bayeux | d° |

On constate que cinq observations d'éclipses de Lune ont été publiées. Dans celle de 1749, Outhier donne un écart de 12 min 15 s entre ses observations et celles effectuées à Paris, ce qui revient à une différence de longitude de 3° 3′ 45″ entre Paris et Bayeux[N 11]. En comparant la longitude trouvée à celle d'aujourd'hui (3° 2′ 23″), on trouve une différence de 1 675 m.
Dans la carte des étoiles des Pléiades, établie en 1750 et publiée en 1755, Outhier donne un complément aux 35 étoiles observées par Le Monnier - Pierre Charles Lemonnier est d'origine normande par son père Pierre Lemonnier né à Saint-Sever (Calvados). Charles possède, à l'époque de l'observation des Pléiades entre 1744 et 1748, une résidence située à 5 km de Bayeux, à Hérils (commune de Maisons) où il mourra en 1799[72].
« La carte des Pléiades, [établie] par M. Outhier, dont trente-cinq des étoiles qui y sont contenues ont été déterminées par les observations de M Lemonnier ; M. l'abbé Outhier a placé les autres par estime et par des alignements pris avec tout le soin possible et plusieurs fois répétés avec les premières. Cet ouvrage est d'autant plus utile que dans de certaines situations des nœuds de la Lune et de ceux des autres planètes, ces étoiles sont souvent éclipsées ou traversées par les unes ou par les autres[73]. »
Mathématiques
En 1755, l'Académie publie un mémoire, en géométrie, sur la quadrature du cercle par approximation, par l'abbé Outhier. Dans la préface des Mémoires de mathématiques et de physique, t. II, on peut lire :
« Tous ceux qui ont la plus médiocre teinture de Géométrie savent qu'on peut toujours, en augmentant les rayons, rendre un secteur d'un moindre nombre de degrés égal à un secteur donné d'un cercle plus petit ; c'est par ce moyen que M. l'abbé Outhier réduit tout cercle et tout secteur donné à un autre secteur dans lequel l'arc peut être aussi petit que l'on voudra. Cette idée a paru simple et ingénieuse. »
Le sujet est développé sur une page avec une figure explicative[74].
Ce problème mathématique est celui qui a résisté le plus longtemps aux mathématiciens. Ils ont mis plus de trois millénaires à étudier le problème, reconnu insoluble par Ferdinand von Lindemann en 1882.
Météorologie et almanach
- En 1756, l'abbé Outhier, « suivant la mode de l'époque[N 12] » relève ses observations météorologiques faites à Bayeux. Elles ont été publiées en 1763[75].
- De 1749 à 1755, il publie, chez Gabriel Briard à Bayeux, un almanach calculé pour le méridien de Bayeux, augmenté de l'état présent de la ville et du diocèse. « Il y calcule l'heure du lever et du coucher du Soleil, du lever et du coucher de la Lune et des planètes, etc., etc. En s'en tenant à peu près aux phénomènes célestes, il n'a fait qu'un almanach aujourd'hui sans intérêt[76]. »
Le Journal d'un voyage au Nord

Lors de l’expédition de Maupertuis en Laponie, l'abbé Outhier, membre participant[N 13], va rédiger son journal qui relate, jour après jour, son implication et ce qu'il a vu de curieux dans ce monde aux confins du cercle polaire[17].
Dédicace et préface
Dans sa dédicace à Monseigneur d'Albert de Luynes, évêque de Bayeux, comme dans la préface de son Journal, Outhier indique qu'il n'a fait ce Journal que pour sa propre satisfaction.
Le style en est extrêmement sec et simple ; assujetti à l'ordre des évènements, Outhier les raconte tels qu'ils sont. « La vérité, la sincérité du récit, la nature des choses que je raconte et qui sont par elles-mêmes quelquefois intéressantes, pourront dédommager le public de ce qui manque à mon style. »
Ayant communiqué son manuscrit à quelques amis, ces derniers l'encouragent, malgré ses réticences et sa modestie, à le publier.
L'ouvrage sera présenté à l'Académie et examiné par Maupertuis et Clairaut. Le , la Compagnie, par la voix de Grandjean de Fouchy secrétaire perpétuel de l'académie royale des sciences, a jugé que l'ouvrage qui relate fidèlement le Voyage des académiciens au Nord était digne d'impression[77].
Vers la Laponie
En 1735, la décision royale de mesurer un arc de méridien vers l'équateur et vers le cercle polaire est prise. M. le comte de Maurepas, secrétaire d'état à la marine « apporte à l'Académie tout le soutien nécessaire pour faire des observations dont le résultat était important pour perfectionner les sciences et pour rendre la navigation encore plus sûre ». M. de Maupertuis s'offrit pour faire le voyage au Cercle Polaire et demanda, entre autres, à Outhier de l'accompagner.
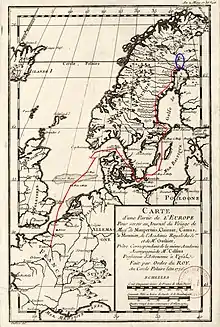
L'abbé se rend à Paris en pour participer à la préparation des instruments et pourvoir à tout le nécessaire pour l'expédition dont le départ est prévu en . Durant cette période, les académiciens du futur voyage, Maupertuis et Clairaut, peu formés aux mesures géodésiques, vont se familiariser avec les instruments et s'exercer à leur usage chez M. Cassini à Thury-sous-Clermont[78] ; peut-être l'abbé s'est-il joint à eux, étant le seul praticien géodésien expérimenté ?
Le départ de Paris a lieu le , direction Dunkerque où ils embarquent à bord d'un petit vaisseau, Le Prudent, le , pour rejoindre Stockholm. Le voyage par mer a lieu sans grandes difficultés - excepté le mal de mer. L'abbé, outre ses impressions personnelles de nouveau navigant et des relevés astronomiques de latitude de l'équipe, joint à son journal des extraits du journal du pilote. L'arrivée à Stockholm, saluée par des tirs de canons, a lieu le . Ils y restent quelques jours et l'abbé en profite pour décrire la ville et en dresser un plan qui sera joint à son ouvrage.
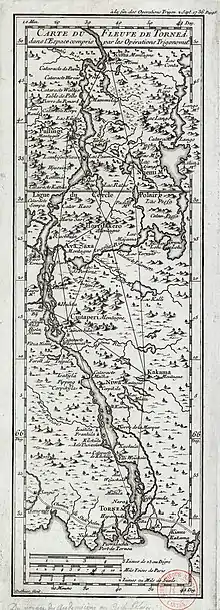
Ayant peu apprécié le voyage par mer, l'équipe poursuit son chemin vers le Nord, par terre, dans deux carrosses achetés pour l'occasion. L'itinéraire passant par différentes bourgades les mène jusqu'à Tornea par des chemins difficiles, tracés à travers la forêt, traversant de nombreux fleuves côtiers sur des bacs plus ou moins improvisés. Ils arrivent à destination le où ils auraient pu voir le soleil de minuit tangent à l'horizon, la ville n'étant qu'à dix-sept lieues environ du cercle polaire. Malheureusement le ciel était brumeux, ils ne virent rien de ce spectacle particulier.
La recherche du théâtre des opérations géodésiques s'avère difficile. Après exploration des environs, le choix se porte sur les « montagnes » entourant le fleuve de Tornea qui suit à peu près le méridien de la ville éponyme.
Le départ pour mener à bien la triangulation a lieu le ; la campagne de repérage et de mesure des triangles durera près de quatre mois.
Campagne d'été : triangulation
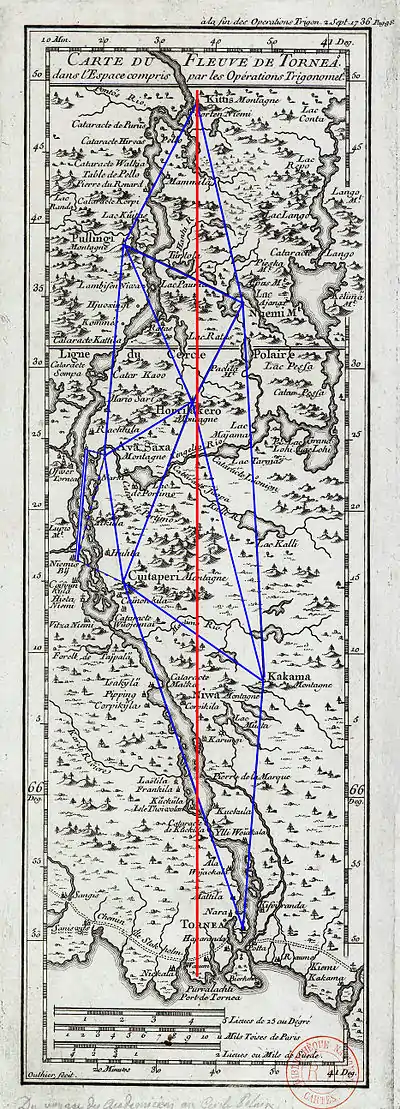
Au nord de Tornea la seule voie de communication est le fleuve. La mission comprenant en tout quinze personnes est accompagnée d'un détachement d'une vingtaine de soldats de l'armée suédoise ; ils embarquent tous, ainsi que le matériel sur sept bateaux à fond plat nécessaires pour passer les nombreux rapides ou cataractes qui jalonnent le parcours. L'accès aux sommets des « montagnes » allant servir de signaux géodésiques s'effectue à pieds, à travers l'enfer d'une forêt primaire et de multiples marais infestés de cousins (moustiques) et moucherons qui dévorent littéralement les voyageurs.
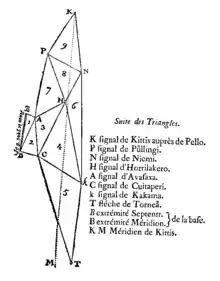
La triangulation va comporter finalement neuf triangles dont les signaux sont constitués de cônes constitués de troncs de sapins écorcés pour être visibles à dix ou douze lieues de leurs points d'élévation. La base, repérée sur le fleuve sera mesurée pendant la campagne d'hiver. La chaîne s'étend sur cent kilomètres environ du sud (Tornea) au nord (Kittis).
Les mesures angulaires sont effectuées à l'aide d'un quart de cercle de deux pieds muni d'un micromètre ; la direction de la méridienne est obtenue en usant d'un « petit instrument anglais » [une lunette méridienne] ; les premières observations stellaires sont réalisées au secteur de Graham sur le site septentrional de Kittis près de Pello. Le la triangulation est terminée, l'équipe, qui a déjà constaté le « gel à glace » le et subi les premières neiges, redescend par le fleuve vers Tornea où ils arriveront le .
Malgré les énormes difficultés sur le terrain pour effectuer les levés géométriques, l'abbé consacre une partie de son temps à noter ses observations sur la vie au Nord[N 14] ; il ébauche aussi dessins, cartes et plans des lieux visités qui agrémenteront plus tard son Journal.
- Quelques illustrations de l'abbé Outhier
 Montagne de Niemi et son signal.
Montagne de Niemi et son signal. Plan de la montagne de Kittis et de Pello.
Plan de la montagne de Kittis et de Pello. Détail des observatoires de Kittis.
Détail des observatoires de Kittis.
Campagne d'hiver : finalisation
Résidant chez l'habitant à Tornea, l'équipe va se consacrer à ses dernières tâches géodésiques. Elles vont s'étaler jusqu'au mois de mai de l'année 1737 et seront entrecoupées par de longs moments de repos compensatoires dus aux conditions climatiques. En effet, sur le terrain, la mission va être confrontée au froid polaire avec des températures extrêmes descendant jusqu'à -40 °C. Dès le début du mois de novembre, les dernières mesures astronomiques sont entreprises mettant en œuvre lunette méridienne (l'« instrument anglais ») et secteur. Ce dernier est mis en place près de l'église de Tornea dont la flèche est le point méridional de la triangulation. Il permet alors de déterminer rapidement la différence de latitude, entre Kittis et Tornea, nécessaire à la détermination d'un degré de latitude.
- Tornea, repère géodésique
 L'église de Tornea, repère géodésique méridional de la triangulation[N 15].
L'église de Tornea, repère géodésique méridional de la triangulation[N 15].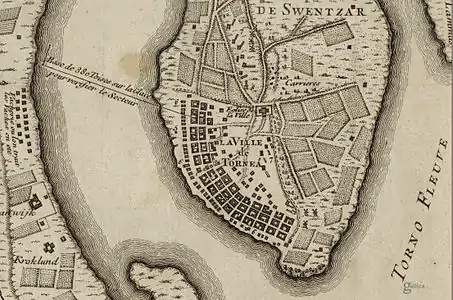 Extrait du plan de Tornea, avec l'église et une base de vérification du secteur.
Extrait du plan de Tornea, avec l'église et une base de vérification du secteur.
Ces travaux sont terminés mi-novembre dans un pays couvert d'une neige qui persistera jusqu'à fin mai et où le fleuve est pris en glace dès le . Les traineaux, le seul moyen de déplacement du moment, prennent alors possession du lit du cours d'eau. Des routes y sont tracées entre deux rangées de sapins plantés pour l'occasion et qui visualisent les voies de circulation sous l'uniformité du manteau neigeux.
Il reste alors à vérifier l'exactitude du secteur et à mesurer, sur le fleuve, la base reconnue au cours de la campagne d'été. Le début du mois de décembre est alors employé au contrôle du secteur et à la fabrication des perches nécessaires à la mesure de la base. Après hésitations et concertation sur les dates des futures opérations à réaliser sur le fleuve, le , la décision est prise d'agir immédiatement.
Le commence le mesurage de la base. Deux équipes travaillent en parallèle. Le froid est intense ; pour l'anecdote Lemonnier se colle la langue en buvant de l'eau-de-vie à un gobelet d'argent et le jour du , Maupertuis a des orteils gelés - sans plus de commentaires de la part d'Outhier. Le 28, les mesures sont terminées : la différence de longueur constatée entre les deux équipes est de quatre pouces sur une distance de 7 406 toises et 5 pieds, résultat donné par l'une des deux équipes.
En janvier les calculs des triangles sont entrepris par tous et de multiples tâches de vérification s'étaleront jusqu'à la mi-mai.
Parmi ces dernières on retiendra : un déplacement épique en traineau vers le signal d'Avasaxa[N 16] où on avait oublié d'effectuer une mesure secondaire, un retour à Pello et Kittis sur le fleuve gelé pour réitérer des observations stellaires au secteur, de multiples mesures concernant le pendule simple et encore d'autres vérifications sur le secteur et la direction de la méridienne.
Les résultats finaux concernant la mesure de l'arc de méridien ne sont pas évoqués, la primeur de ces informations revenant à Maupertuis qui entretiendra le suspens jusqu'après son retour en France où il dira devant l'Académie que « La terre est aplatie aux pôles ».
Entre ces différentes activités géodésiques hivernales, Outhier travaille à la mise au net de ses cartes et note ses observations du moment : description de Tornea et des environs avec ses habitations, ses cultures, ses arbres, ses fruits, ses plantes ; description aussi des mœurs des Lapons (traineaux, skis…) et de leurs lieux de vie ; étude des rennes, ressource fondamentale de la population, etc.
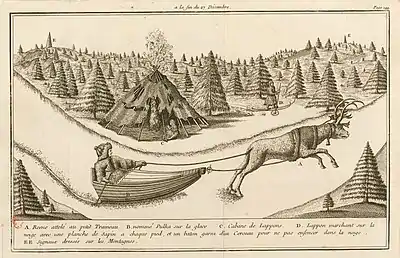
Il est à noter aussi qu'Outhier souligne l'interdiction qui lui a été signifiée par M. de Maurepas et M. l'ambassadeur de France de ne « point du tout dire la messe » pour éviter de choquer des habitants de religion luthérienne. Il décrit néanmoins leurs façons particulières de célébrer les fêtes religieuses, auxquelles il a parfois assisté et qui sont les mêmes que celles de la religion catholique.
Au milieu du mois de mai, le dégel s'annonce, les travaux sont terminés, l'équipe s'apprête alors au départ qui aura lieu le .
Retour en France
La mission française va se diviser en deux groupes. Le , une équipe comprenant Maupertuis et Clairaut accompagne le matériel - instruments et bagages - qui est embarqué sur un vaisseau à destination de Stockholm. L'autre équipe est composée de Camus, Celsius, Lemonnier et l'abbé Outhier ; répugnant à prendre la mer, ils partiront le lendemain en carrosse.
Le 13, après un début de voyage mouvementé à cause de mauvais chevaux, la deuxième équipe est surprise de rencontrer à terre Maupertuis et ses compagnons tout près de Pitea. Pris dans une tempête, ils ont fait naufrage et se sont échoués, heureusement sans dommages. Après réparations, tout le monde repart le .
Entre le et le , ils s'arrêtent vers Falun où ils visitent des mines de cuivre, une manufacture de laiton et des mines d'argent. Ils arrivent à Stockholm le . Ils y sont reçus par le roi qui les invite à une grande fête, donnée le 15, à l'occasion de la célébration de la sainte Ulrique patronne de la reine.
Le , Maupertuis et quelques personnes de l'équipe s'embarquent pour Amsterdam. Camus, Clairaut, Lemonnier et l'abbé continuent leur voyage en carrosse, laissant Celsius dans son pays. Ils passent le Sund et arrivent à Copenhague le 25 où ils restent cinq jours. Puis, après avoir traversé le grand Belt et le petit Belt, ils passent par Hambourg pour retrouver Maupertuis à Amsterdam.
 Plan de la ville de Pitea en 1736.
Plan de la ville de Pitea en 1736. Vue de la ville de Falun ou Coppenberg (1737).
Vue de la ville de Falun ou Coppenberg (1737). Tour astronomique de Copenhague en 1737.
Tour astronomique de Copenhague en 1737.
Ils prendront alors la direction de Paris en passant par Rotterdam, Anvers et Bruxelles.
Le lendemain de leur arrivée, ils sont reçus à Versailles par le comte de Maurepas. Il les présente au cardinal Fleury puis au Roi. Le premier ministre les félicitera « de la parfaite union qui avait régné entre eux pendant le voyage ».
Le , Maupertuis « rend compte à l'Académie des opérations trigonométriques et fait voir sur de grandes figures la suite de nos triangles ».
Le vendredi , après une absence de vingt-et-un mois, comme le dira modestement l'abbé, « il retourne auprès de Monseigneur l'Évêque de Bayeux reprendre son premier train de vie ».
Observations personnelles
L'abbé Outhier, à la suite de son Journal, joint ses observations propres, « avec un calcul très simple de ses triangles ».
On y trouve sommairement sur une trentaine de pages : l'observation des triangles, leurs calculs, les observations astronomiques effectuées à l'aide du secteur et pour finir la longueur du méridien au cercle polaire.
Notes et références
Notes
- Il a sans doute disparu avec le père Rousselot, le curé de La Marre décédé en 1710.
- Pour mémoire, on rappelle qu'entre le 16 juillet et le 7 août 1731, le nom du curé de Montain est changé dans les registres de la paroisse.
- Cette perpendiculaire, menée de Strasbourg à Saint-Malo est une chaîne de triangles géodésiques qui fera partie de l'ossature de la carte de Cassini.
- Celsius est aujourd'hui connu pour l'échelle thermométrique qui porte son nom.
- Maupertuis dit simplement de lui dans la préface de La figure de la Terre « M. l'abbé Outhier, dont la capacité dans l'ouvrage que nous allions faire était connue… »
- Quand Maupertuis se rend à Berlin, sous l'impulsion de Maurepas, il est exclu de l'Académie des sciences de Paris et son image française est très mauvaise ; Outhier, correspondant de Cassini et attaché à son évêque proche de la Cour, a dû faire un choix difficile.
- Voir infra la carte du diocèse de Bayeux.
- C'est-à-dire la pointe du Cotentin.
- L'évêque de Bayeux deviendra archevêque de Sens, en 1753, à la mort de ce dernier.
- À Sens, où Luynes sera nommé archevêque en 1753, il sera tracé par le prélat deux méridiennes horizontales, toujours situées dans les étages de ses résidences.
- 15° de longitude correspondent à un décalage de 1 h.
- Les premiers relevés officiels de météorologie semblent être le fait de Maraldi ; ils ont été publiés dans les Mémoires de l'Académie.
- Voir la section Le Voyage au Nord, 1736-1737 pour les participants.
- On peut citer comme descriptions, en vrac : un arc-en-ciel triple, différents types de moulins, un moyen de chauffage particulier, la manière de faucher les foins, la manière de vivre des chevaux, la description de villages, les bains finnois (sauna).
- Voir une vue de l'église actuelle.
- Maupertuis décrira aussi ce périple d'une façon mémorable et jubilatoire dans son ouvrage La Figure de la Terre.
Références
- J. Richard 1926, p. 113.
- Osmo Pekonen 2010, p. 5.
- Mario Morisi 2010, p. 7-17.
- Osmo Pekonen 2010, p. 5-6,20-21.
- Mario Morisi 2010, p. 16-17.
- J. Richard 1926, p. 113-114..
- Osmo Pekonen 2010, p. 6, 21.
- Voir sommairement son histoire : accès en ligne
- Pour ces « premières années scientifiques » voir principalement J. Richard 1926, p. 114 ; Osmo Pekonen 2010, p. 6-8.
- Académie des sciences (France) 1699-1786, p. année 1735.
- D. Monnier, Les Jurassiens recommandables, Lons-le-Saunier, (lire en ligne), p. 288.
- Académie des sciences, membres, in memoriam… lire en ligne
- Voir les détails dans la page « Carte de Cassini »
- accès en ligne.
- Osmo Pekonen 2010, p. 8.
- Charma & Mancel, Le père André, t. II, Paris, Hachette, (lire en ligne), p. 21-22.
- M. Outhier 1744.
- Élisabeth Badinter 1999, p. 95.
- Académie des sciences (France), Procès-verbaux, Paris, (lire en ligne), p. 571 ; en clair, voir une page de la Connaissance des temps de 1758 : accès en ligne
- Cassini de Thury, Description géométrique de la France, Paris, (lire en ligne), p. 9.
- Osmo Pekonen 2010, p. 9 qui cite la correspondance de Maupertuis ; Élisabeth Badinter 1999, p. 325 à 364 pour Maupertuis et Berlin.
- Jean Cousin, L'Académie des sciences, belles-lettres et arts de Besançon, deux cents ans de vie comtoise, 1752-1952, essai de synthèse, Besançon, J. Ledoux, , 253 p. (BNF 31976518), p. 89.
- Osmo Pekonen 2010, p. 11.
- J. Richard 1926, p. 137-138..
- Bibliothèque du Chapitre de Bayeux, ms. 278, fo 224
- J. Richard 1926, p. 138-141..
- Laffetay, Histoire du diocèse de Bayeux. XVIIIe et XIXe siècles, Imprimerie H. Grobon et O. Payan, (lire en ligne), p. 39-40.
- Bulletin de la société des antiquaires de Normandie, t. XXII, Caen, (lire en ligne), p. 142-144.
- 13 rue Montfiquet, accès en ligne
- Société des sciences, arts et belles-lettres de Bayeux, vol. 11, (lire en ligne).
- Histoire de l'Académie royale des sciences, 1727, lire en ligne.
- M. Gallon 1735, p. 15-18.
- M. Gallon 1735, p. 19-23.
- voir le P.V. du 26 juillet 1727
- voir le P.V. du 2 août 1727
- le premier : accès en ligne. ; le second : accès en ligne.
- Voir le globe parmi d'autres images d'horlogerie : accès en ligne.
- Voir le P.V. de 1732 : accès en ligne.
- Mémoire : accès en ligne.
- Jacques Cassini 1735, p. 405, lire en ligne
- Jacques Cassini 1735, lire en ligne
- Jacques Cassini 1735, p. 405.
- Cassini de Thury 1783, p. 157 et 31.
- Cassini de Thury 1741, p. 134.
- Cassini de Thury 1741, p. 120
- Voir la base dans : Cassini de Thury 1783, p. 33 ; voir sa localisation sur la carte de France de 1744, accès en ligne.
- Pour cette triangulation, voir : Cassini de Thury 1783, p. 159-163.
- Monique Pelletier, Les cartes des Cassini, la science au service de l'état et des provinces, Paris, CTHS, (ISBN 978-2-7355-0786-3), p. 115
- lire en ligne
- Carte de Bayeux, accès en ligne
- Carte d'Ons-en-Bray, accès en ligne.
- Carte de Sens , accès en ligne.
- Carte septentrionnale de l'évêché de Meaux
- M. Meynier, Odomètre ou compte-pas, t. IV, Paris, coll. « Machines et inventions approuvées par l'Académie royale des sciences », 1720-1726 (lire en ligne), p. 93-106.
- Machines et inventions approuvées par l'Académie en 1742, Paris, coll. « Histoire de l'Académie royale des sciences », (lire en ligne), p. 143-146.
- Abbé Outhier, Odomètre, t. VII, Paris, coll. « Recueil des machines approuvées par l'Académie », (lire en ligne), p. 175-183.
- d'Alembert…, Encyclopédie méthodique : Mathématiques, t. II, Paris, Panckoucke, (lire en ligne), p. 483-484.
- Charma & Mancel, Le père André, t. II, Paris, Hachette, (lire en ligne), p. 22.
- Jacques Cassini 1735, p. 404.
- Jacques Cassini, Observations de l’éclipse de Jupiter, Paris, coll. « Histoire de l’Académie royale des Sciences », (lire en ligne), p. 415-416.
- Sur les trois méridiennes citées, voir : Gérard Aubry, Les méridiennes du cardinal de Luynes, vol. 33, Paris, SAF, coll. « Cadran-Info », .
- Académie des sciences (France), Histoire de l'Académie royale des sciences, Paris, (lire en ligne), p. 511.
- Académie des sciences (France), Histoire de l'Académie royale des sciences, Paris, (lire en ligne), p. 415.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. II, (lire en ligne), p. 307.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. II, (lire en ligne), p. 309.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. II, (lire en ligne), p. 311.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. II, (lire en ligne), p. 313.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. II, (lire en ligne), p. 607-608 et vue 684.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. VI, (lire en ligne), p. 134.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. VI, (lire en ligne), p. 133.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. VI, (lire en ligne), p. 176.
- Jean-Baptiste Delambre, Histoire de l'astronomie au XVIIIe siècle, Paris, (lire en ligne), p. 237.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. II, (lire en ligne), p. XVIII.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. II, (lire en ligne), p. XV et 332-333.
- Académie des sciences (France), Mémoires de mathématiques et de physique, t. IV, (lire en ligne), p. 612
- Bulletin de la société des antiquaires de Normandie, t. XXII, Caen, (lire en ligne), p. 144 et Association normande, Annuaire des cinq départements de l'ancienne Normandie, Caen, (lire en ligne), p. 547-548.
- Voir la page du 25/04/1744 du registre des P.V. de l'Académie : lire en ligne
- Jean-Pierre Martin, Une histoire de la Méridienne : Textes, enjeux, débats et passions autour du Méridien de Paris, 1666-1827, Cherbourg, Isoète, , p. 42.
Annexes
Bibliographie
- M. Outhier, Journal d'un voyage au Nord, Paris, (lire en ligne).
- J. Richard, L'abbé Outhier : un franc-comtois au cercle poaire arctique en 1736-1737, Académie des sciences, belles-lettres & arts de Besançon, coll. « Séances publiques », , chapitre du 3e trimestre.
 .
. - Osmo Pekonen, La rencontre des religions autour du voyage de l'abbé Réginald Outhier en Suède en 1736-1737 : Thèse doctorale de l'Université de Laponie, Rovaniemi: Lapland University Press, (ISBN 978-952-484-390-4), chapitre 4.
 .
. - Mario Morisi, La boue et les étoiles : L'abbé Renaud Outhier un prêtre Sçavans au Siècle des Lumières, Besançon, Sekoya, , 197 p. (ISBN 978-2-84751-076-8).
 , roman dérivé des informations contenues dans la thèse doctorale d'Osmo Pekonen et très proche de la biographie d'Outhier, avec des informations non publiées à la date de parution de l'ouvrage.
, roman dérivé des informations contenues dans la thèse doctorale d'Osmo Pekonen et très proche de la biographie d'Outhier, avec des informations non publiées à la date de parution de l'ouvrage. - Jean-Jacques Levallois, Mesurer la Terre : 300 ans de géodésie française, Paris, A.F.T., , 389 p. (ISBN 2-907586-00-9).
- Élisabeth Badinter, Désirs de gloire, 1735-1751 : Les passions intellectuelles, Paris, Fayard, , 663 p. (ISBN 978-2-253-08467-9).
 .
. - Cassini de Thury, Description géométrique de la France, Paris, (lire en ligne).
Références de l'Académie des sciences :
- Académie des sciences (France), Histoire de l'Académie royale des sciences, Paris, 1699-1786 (lire en ligne).
- Jacques Cassini, De la carte de France et de la perpendiculaire à la méridienne de Paris : année 1733, Paris, coll. « Histoire de l'Académie royale des sciences », (lire en ligne).
 .
. - Cassini de Thury, Sur les opérations géométriques faites en France dans les années 1737 et 1738 : année 1739, Paris, coll. « Histoire de l'Académie royale des sciences », (lire en ligne).
 .
.
- Jacques Cassini, De la carte de France et de la perpendiculaire à la méridienne de Paris : année 1733, Paris, coll. « Histoire de l'Académie royale des sciences », (lire en ligne).
- M. Gallon, Machines et inventions approuvées par l'Académie : depuis 1727 jusqu'à 1731, t. V, Paris, (lire en ligne), p. 15-23.
 .
.
Articles connexes
Liens externes
- André Balland, La terre mandarine : Journal d'un voyage au Nord pour déterminer la figure de la Terre par M. l'abbé Réginald Outhier, Seuil, (ISBN 2-02-022478-X, BNF 35736632). Il s'agit du texte intégral d'Outhier, à l'orthographe modernisée. Il est complété par une mise en situation dans le contexte scientifique de l'époque, que ce soit avant ou après Le voyage au Nord ;
- C. Fournerat, Recherches sur les personnes qui dans le département de l'Yonne se sont occupées d'astronomie, vol. 16, Auxerre, coll. « Bulletin de la société des sciences historiques et naturelles de l'Yonne », (lire en ligne), p. 47-51.