Pulvérisation (mathématiques)
Le concept de pulvérisation d'un ensemble de points joue un rôle important dans la théorie de Vapnik-Chervonenkis, également connue sous le nom de théorie VC (suivant la translitération anglaise). La pulvérisation et la théorie VC sont utilisées dans l'étude des processus empiriques ainsi qu'en théorie de l'apprentissage automatique statistique.
La pulvérisation consiste à pouvoir distinguer des données positives (+) et des données négatives (-). Le terme a été introduit en 1975 par J. M. Steele dans sa thèse de doctorat, à l'université Stanford.
Principe
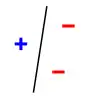
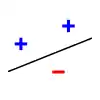
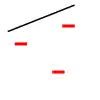
Expliquons le principe de la pulvérisation en prenant comme modèle de classification une droite dans le plan, où les données sont représentées par des points étiquetés par + ou - dans le plan. On étudie si une droite peut séparer les données positives (+) des données négatives (-). Si on prend 3 points non alignés, une droite peut les pulvériser. En effet, comme le montrent les trois images ci-dessous, on place une droite de façon que les données positives soient d'un côté et les données négatives de l'autre. Ci-dessous, pour la pulvérisation de 3 points, on montre seulement 3 des 8 étiquetages possibles (1 seule possibilité de les étiqueter tous les 3 positifs, 3 possibilités d'en étiqueter 2 sur 3 positifs, 3 possibilités d'en étiqueter 1 sur 3 positif, 1 possibilité de n'en étiqueter aucun positif).
Cependant, une droite ne peut pas pulvériser 4 points. En effet, on peut trouver un étiquetage des points de façon qu'aucune droite sépare les données positives et négatives. Il est important de noter que l'on peut choisir les positions des points qu'on va pulvériser avec une droite, mais qu'on ne peut pas ensuite modifier ces positions lorsqu'on permute leur étiquetage.
 |
 |
 |
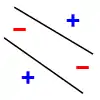 |
| Pulvérisation de 3 points | Lorsqu'il y a 4 points, la pulvérisation est impossible | ||
Dans la théorie VC, on dira que la dimension VC de la droite est de 3.
Définition
Soient C une classe d'ensembles et A un ensemble de points. On dit que C pulvérise A si et seulement si, pour tout sous-ensemble T de A, il existe un élément U appartenant à C tel que
Dans l'exemple des droites dans le plan, la classe est en fait l'ensemble des demi-plans. Dans la définition, le sous-ensemble T de A correspond à l'ensemble des points étiquetés positivement. L'égalité signifie que les points de A qui sont dans le demi-plan U sont exactement les exemples positifs.
Ceci équivaut encore à dire que C pulvérise A si et seulement si l'ensemble des parties de l'ensemble A, P(A), est égal à l'ensemble { U ∩ A | U ∈ C }.
Exemples
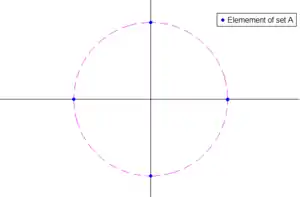
Fixons un ensemble A de quatre points du cercle unité. Par exemple, les quatre points bleu sur la figure de droite.
Classe des disques
On voudrait savoir s'il est pulvérisé par la classe C de tous les disques.
- Si tous les points sont étiquetés positivement, on peut placer un disque qui couvre tous les points.
- Si un point est positif et les trois autres sont négatifs. On place alors un disque qui uniquement ce point. (Figure (a) ci-dessous)
- Si deux points adjacents sont positifs, nous plaçons un disque qui couvre exactement ces deux points (Figure (b) ci-dessous)
- Par contre, nous remarquons que le cas où exactement deux points opposés sont positifs est problématique. Il est impossible de placer un disque qui couvre exactement deux points opposés. En effet, le disque couvrirait également un point négatif (Figure (c) ci-dessous).
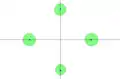 (a) Chaque point peut être isolé par un disque (les quatre sont montrés).
(a) Chaque point peut être isolé par un disque (les quatre sont montrés). (b) Chaque sous-ensemble de points adjacents peut être isolé par un disque (un seul est montré).
(b) Chaque sous-ensemble de points adjacents peut être isolé par un disque (un seul est montré). (c) Un sous-ensemble de points opposés ne peut pas être isolé par un disque.
(c) Un sous-ensemble de points opposés ne peut pas être isolé par un disque.
Comme certaines parties de A ne peuvent pas être isolées par les cercles de C, on peut en conclure que A n'est pas pulvérisé par C. On peut aussi prouver qu'aucun ensemble A de quatre points ne peut l'être.
Classe des ellipses
Si maintenant on prend C égal à la classe des intérieurs d'ellipses (que l'on appelle ellipse dans la suite), on arrive à dissocier les points de chaque partie de A. Donc notre ensemble particulier de quatre points est pulvérisé par la classe des ellipses.
 Des points opposés de A sont maintenant dissociables (une montrée sur les deux).
Des points opposés de A sont maintenant dissociables (une montrée sur les deux). Chaque sous-ensemble de trois points de A est aussi dissociable par une ellipse (une montrée sur quatre).
Chaque sous-ensemble de trois points de A est aussi dissociable par une ellipse (une montrée sur quatre).
Plus généralement, n'importe quel ensemble fini de points du cercle unité peut être pulvérisé par l'ensemble des ensembles convexes.
Coefficient de pulvérisation
Pour mesurer la richesse d'une collection d'ensembles, on utilise le concept de « coefficients de pulvérisation » (également appelés « fonction de croissance »). Pour une collection d'ensembles Ω, où Ω est un ensemble, on définit le nième coefficient de pulvérisation de par
où « card » est le cardinal, c'est-à-dire, le nombre d'éléments d'un ensemble.
De cette définition découlent les propriétés suivantes :
- 1. pour tout n.
- 2. , si et seulement s'il existe un ensemble de cardinal n pulvérisé par C.
- 3. S'il existe tel que , alors pour tout (en d'autres termes, une classe d'ensembles qui ne peut pulvériser aucun ensemble à N éléments ne pourra pas non plus pulvériser d'ensemble plus grand).
Classe de Vapnik-Chervonenkis
La dimension VC d'une classe C est définie par
- ou, de manière alternative, par :
On remarquera qu'on a : .
On dira que la dimension VC d'une classe est infinie si pour tout n il existe un ensemble à n éléments pulvérisé par C (on a alors, pour tout entier naturel n, ).
Les classes de dimension VC finie sont appelées classes de Vapnik-Chervonenkis ou classes VC. Une classe d'ensembles est une classe uniformément Glivenko-Cantelli si et seulement si c'est une classe VC.
Sources
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Shattered set » (voir la liste des auteurs).
- [PDF] Cours sur la theorie de l’apprentissage statistique (selon V. Vapnik) de François Denis, de l'Équipe Bases de Données et Apprentissage du Laboratoire d’Informatique Fondamentale de Marseille
- (en) cours sur la dimension VC de Andrew Moore
- (en) V. Vapnik et A. Chervonenkis. "On the uniform convergence of relative frequencies of events to their probabilities." (De la convergence uniforme des fréquences relatives des événements vers leur probabilité) Theory of Probability and its Applications, 16(2):264--280, 1971.
- (en) A. Blumer, A. Ehrenfeucht, D. Haussler, et M. K. Warmuth. "Learnability and the Vapnik-Chervonenkis dimension." (Capacité d'apprentissage et dimension de Vapnik-Chervonenkis) Journal of the ACM, 36(4):929--865, 1989.
- (en) Wencour, R.S., R.M. Dudley (1981), "Some special Vapnik-Chervonenkis classes"(Classes spéciales de Vapnik-Chervonenkis), Discrete Math, 33, 1981, 313-318.
- (en) Steele, J.M. (1975), "Combinatorial Entropy and Uniform Limit Laws"(Entropie Combinatoire et lois de convergence uniforme), thèse de doctorat de mathématiques de l'université Stanford.
- (en) Steele, J.M. (1978), "Empirical discrepancies and subadditive processes"(Divergences empiriques et processus sous-additifs), Annals of Probability, 6, 118--227.













